📢 preface

• 🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻
• 🌲 Punching out an algorithm problem every day is not only a learning process, but also a sharing process 😜
• 🌲 Tip: the problem-solving programming languages in this column are C# and Java
• 🌲 To maintain a state of learning every day, let's work together to become the great God of algorithm 🧐!
• 🌲 Today is the third day of punching out the force deduction algorithm 🎈!
• 🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻

🌲 Sample of original question

Given a string s, please find the length of the longest substring that does not contain duplicate characters.

Example 1:

• Enter: s = "abcabcbb"
• Output: 3
• Explanation: because the longest substring without repeated characters is "abc", its length is 3.

Example 2:

• Input: s = "bbbbb"
• Output: 1
• Explanation: because the longest substring without repeated characters is "b", its length is 1.

Example 3:

• Input: s = "pwwkew"
• Output: 3
• Explanation: because the longest substring without repeated characters is "wke", its length is 3.
  Please note that your answer must be the length of the substring, "pwke" is a substring, not a substring.

Tips:

• 0 <= s.length <= 5 * 104
• s consists of English letters, numbers, symbols and spaces

🌻 C# method 1: index search

First, directly traverse all characters, and then store the value when encountering repeated characters. At the same time, process the List to find the next team.

public class Solution {
public int LengthOfLongestSubstring(string s) {

        List<char> ls = new List<char>();
        int n = s.Length;
        int intMaxLength = 0;

        for (int i = 0; i < n; i++)
        {
            if (ls.Contains(s[i]))
            {
                ls.RemoveRange(0, ls.IndexOf(s[i]) + 1);
            }
            ls.Add(s[i]);
            intMaxLength = ls.Count > intMaxLength ? ls.Count : intMaxLength;
        }

        return intMaxLength;
    }
    }

results of enforcement

The execution passed, the execution time was 76ms, and the memory consumption was 25MB

🌻 C# method 2: sliding window

Sliding Window algorithm can be used to solve the sub element problem of string (array), find the continuous sub interval that meets certain conditions, convert the nested loop problem into a single loop problem, and reduce the time complexity.

The sliding window algorithm requires double pointers. When traversing the string (array), both pointers start at the origin and move to the end one after the other. The substring (subarray) clamped between the two pointers is like a window, and the size and coverage of the window will change with the movement of the front and rear pointers.

How to move the window needs to be determined according to the problem to be solved. Through the movement of the left and right pointers, traverse the string (array) to find the continuous sub interval that meets the specific conditions.

public class Solution {
    public int LengthOfLongestSubstring(string s) {
        HashSet<char> letter = new HashSet<char>();// A hash set that records whether each character has occurred
        int left = 0,right = 0;//Initializes the left and right pointers to the first character of the string
        int length = s.Length;
        int count = 0,max = 0;//count records the length of the substring after each pointer movement
        while(right < length)
        {
            if(!letter.Contains(s[right]))//Right pointer character not repeated
            {
                letter.Add(s[right]);//Add this character to the collection
                right++;//The right pointer continues to move right
                count++;
            }
            else//The right pointer character repeats, and the left pointer starts to move right until there is no duplicate character (that is, the left pointer moves to the right of the duplicate character (left))
            { 
                letter.Remove(s[left]);//Removes the current left pointer character from the collection
                left++;//Shift left pointer to right
                count--;
            }
            max = Math.Max(max,count);
        }
        return max;
    }
}

results of enforcement

The execution passed. The execution time was 68ms and the memory consumption was 25.6MB

🌻 Java method 1: sliding window

Ideas and algorithms
This is in the official solution of force buckle. Come and have a look directly!
Let's use an example to consider how to pass this problem in a better time complexity.

We might as well take the string \ texttt{abcabcbb}abcabcbb in example 1 as an example to find the longest substring starting from each character and not containing repeated characters, and the longest string is the answer. For the string in example 1, we list these results, where the selected character and the longest string are represented in parentheses:

• The longest string starting with \ texttt{(a)bcabcbb}(a)bcabcbb is \ texttt{(abc)abcbb}(abc)abcbb;
• The longest string starting with \ texttt{a(b)cabcbb}a(b)cabcbb is \ texttt{a(bca)bcbb}a(bca)bcbb;
• With \ texttt{ab © abcbb}ab © The longest string starting from abcbb is \ texttt{ab(cab)cbb}ab(cab)cbb;
• The longest string starting with \ texttt{abc(a)bcbb}abc(a)bcbb is \ texttt{abc(abc)bb}abc(abc)bb;
• The longest string starting with \ texttt{abca(b)cbb}abca(b)cbb is \ texttt{abca(bc)bb}abca(bc)bb;
• With \ texttt{abcab © bb}abcab © The longest string starting from BB is \ texttt{abcab(cb)b}abcab(cb)b;
• The longest string starting with \ texttt{abcabc(b)b}abcabc(b)b is \ texttt{abcabc(b)b}abcabc(b)b;
• The longest string starting with \ texttt{abcabcb(b)}abcabcb(b) is \ texttt{abcabcb(b)}abcabcb(b).

In this way, we can use "sliding window" to solve this problem:

• We use two pointers to represent the left and right boundaries of a substring (or window) in the string. The left pointer represents the "starting position of enumeration substring" in the above, and the right pointer is r_kr k in the above;

• In each step of operation, we will move the left pointer to the right by one grid, indicating that we start enumerating the next character as the starting position, and then we can constantly move the right pointer to the right, but we need to ensure that there are no duplicate characters in the substring corresponding to the two pointers. After the movement, this substring corresponds to the longest substring starting with the left pointer and not containing duplicate characters. We record the length of this substring;

• After enumeration, the length of the longest substring we find is the answer.

Determine duplicate characters

In the above process, we also need to use a data structure to judge whether there are duplicate characters, The commonly used data structure is hash Set (i.e. std::unordered_set in C + +, HashSet in Java, Set in Python and Set in JavaScript). When the left pointer moves to the right, we remove a character from the hash Set. When the right pointer moves to the right, we add a character to the hash Set.

So far, we have solved the problem perfectly

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // A hash set that records whether each character has occurred
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // The right pointer, whose initial value is - 1, is equivalent to that we are on the left side of the left boundary of the string and have not started moving
        int rk = -1, ans = 0;
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // The left pointer moves one space to the right to remove a character
                occ.remove(s.charAt(i - 1));
            }
            while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
                // Keep moving the right pointer
                occ.add(s.charAt(rk + 1));
                ++rk;
            }
            // Characters i to rk are a very long non repeating character string
            ans = Math.max(ans, rk - i + 1);
        }
        return ans;
    }
}

results of enforcement

The execution passed. The execution took 6ms and the memory consumption was 38.3 MB

🌻 Java method 2: traversal

General idea
Traverse the string, record with I value each time, do not backtrack the I value, and use flag to record the position of repeated characters found in the traversal process. If a duplicate character is encountered, i-flag is the length of the substring. At this time, the flag is relocated to the position of the duplicate character in the substring, and I continues to traverse back. Here, length and result record length. I think the code can be a little more concise, but it seems to be confused?

graphic

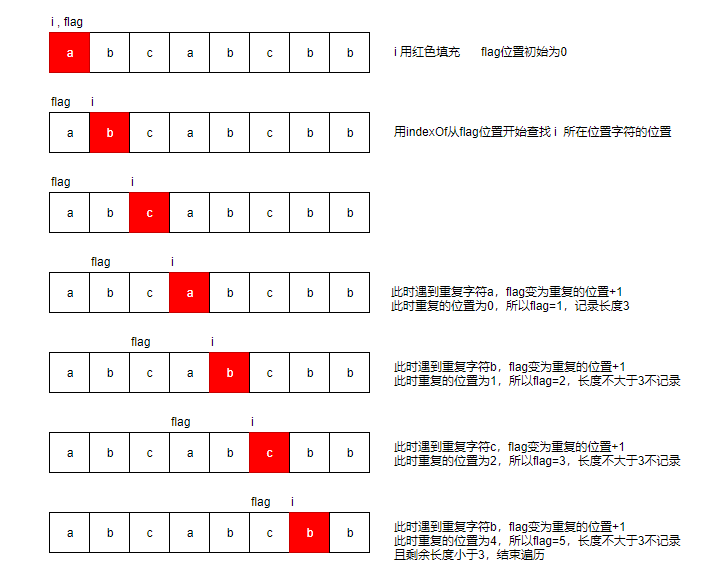
class Solution {
  public int lengthOfLongestSubstring(String s) {
        //a b c a b c d a d e
        //0 1 2 3 4 5 6 7 8 9
        int maxSize = 0;
        //Record the position where ASCII characters appear, with characters as subscripts
        int[] dict = new int[128];
        //For ease of understanding, set all the contents of the array to - 1, and then start from 0 when recording for ease of understanding
        Arrays.fill(dict, -1);
        //A value used to record where duplicate ASCII characters appear
        int repeatValue = -1;
        // Current subscript
        int i = 0;
        int ASCII;
        while (i < s.length()) {
            ASCII = s.charAt(i);
            //If the value of the current position > repeatvalue, it proves that the current position has been assigned a value once and the characters are repeated
            if (dict[ASCII] > repeatValue)
                //Update repeatValue to the subscript of the previous assignment
                repeatValue = dict[ASCII];
            //Assign the current subscript to the corresponding position of the array
            dict[ASCII] = i;
            //I - repeatvalue (remove duplicates)
            // For example, the calculation of three a's in abcabcdade ABCA - a (3 - 0) = BCA abcabcda - ABCA (7 - 3) = bcda
            maxSize = Math.max(maxSize, i - repeatValue);
            //s.length() - repeatValue - 1 judge whether it is necessary to continue the cycle for the remaining number
            //For example, the last a of abcabcdade (when I = 7, repeatvalue = 3), abcabcdade - abca(10-3-1) = bcdade, there are at most six digits left
            //For example, the last d of abcabcdade (when I = 8, repeatvalue = 6), abcabcdade - abcabcd(10-6-1) = ade, and at most three digits remain
            if (maxSize >= s.length() - repeatValue - 1) {
                return maxSize;
            }
            i++;
        }
        return maxSize;
    }
}

results of enforcement

The execution passed. The execution took 2ms and the memory consumption was 42.68 MB

💬 summary

• Today is the third day of punching out the force deduction algorithm!
• This paper uses C# and Java programming languages to solve problems
• Some methods are also written by Likou God, and they are also shared while learning. Thanks again to the algorithm bosses
• That's the end of today's algorithm sharing. See you tomorrow!