1, Title Requirements

• Give you a matrix with m rows and n columns. Please return all the elements in the matrix in a clockwise spiral order.
• Example 1:

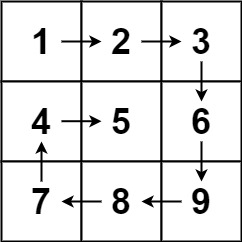
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output:[1,2,3,6,9,8,7,4,5]

• Example 2:

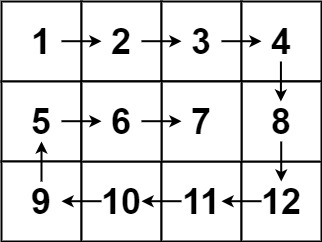
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output:[1,2,3,4,8,12,11,10,9,5,6,7]

• Tips:
• • m == matrix.length
• • n == matrix[i].length
• • 1 <= m, n <= 10
• • -100 <= matrix[i][j] <= 100

2, Solving algorithm

① Loop traversal

• Traverse the print matrix layer by layer from the outside to the inside. After printing the outermost circle, there is still a matrix inside.
• Count the number of layers of the matrix. Each layer will occupy at most two rows or columns, and at least one row or column of elements. Only one layer or column is also considered as one layer. The layering is shown in the figure below:

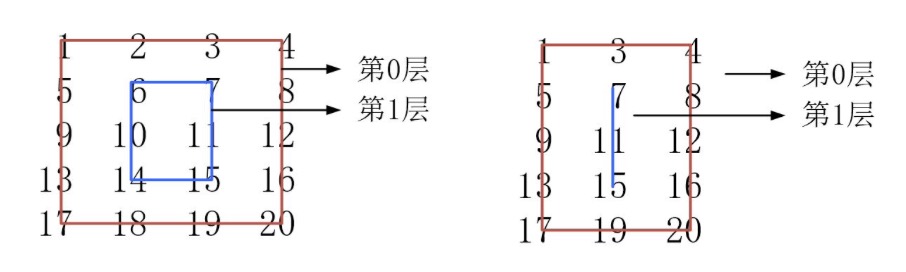
int m = matrix.length;
int n = matrix[0].length;
int count = (Math.min(m, n)+1)/2;

• Start printing the matrix elements of layer i, as shown in the figure below. When printing the matrix of layer i, it will go through four cycles:

• 1st: from left to right

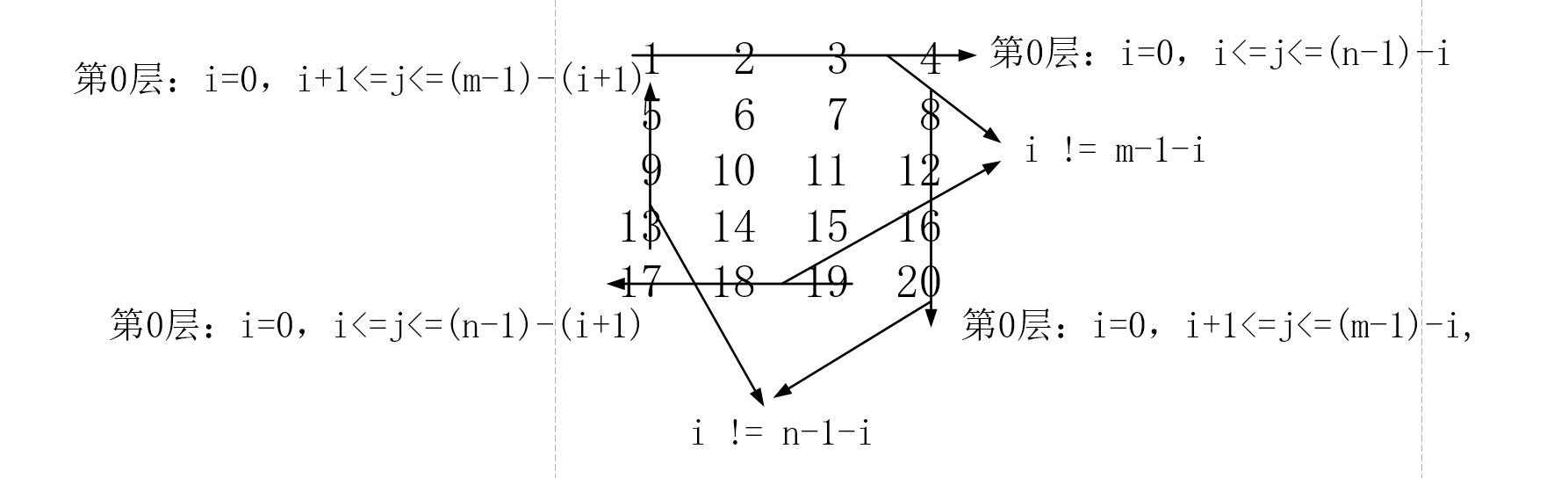
for (int j = i; j < n-i; j++) {
    list.add(matrix[i][j]);
} 

• 2nd: from top to bottom

for (int j = i+1; j < m-i; j++) {
    list.add(matrix[j][(n-1)-i]);
}

• The third: from right to left, if there is only one line in this layer, the first cycle has printed this line, so there is no need to print here, that is (m-1-i)= i:

for (int j = (n-1)-(i+1); j >= i && (m-1-i != i); j--) {
    list.add(matrix[(m-1)-i][j]);
}

• The fourth: from bottom to top, if there is only one column in this layer, the second cycle has printed the column. There is no need to print here, that is (n-1-i)= i

for (int j = (m-1)-(i+1); j >= i+1 && (n-1-i) != i; j--) {
    list.add(matrix[j][i]);
}

• Java example:

public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<Integer>();
        if(matrix == null || matrix.length == 0)
    		return list;
        int m = matrix.length;
        int n = matrix[0].length;
        int i = 0; 

        // Count the number of layers of the matrix from outside to inside. If the matrix is not empty, its number of layers is at least 1
        int count = (Math.min(m, n)+1)/2;
        // Traverse from outside to inside and print data layer by layer
        while(i < count) {
        	for (int j = i; j < n-i; j++) {
				list.add(matrix[i][j]);
			}
        	for (int j = i+1; j < m-i; j++) {
				list.add(matrix[j][(n-1)-i]);
			}
        	
        	for (int j = (n-1)-(i+1); j >= i && (m-1-i != i); j--) {
				list.add(matrix[(m-1)-i][j]);
			}
        	for (int j = (m-1)-(i+1); j >= i+1 && (n-1-i) != i; j--) {
				list.add(matrix[j][i]);
			}
        	i++;
        }    
        return list;
    }

• C + + example:

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int sizey = matrix.size();
        int sizex = matrix[0].size();
        // Number of traversal cycles
        int loop = min(sizey, sizex) / 2;
        // Traverse the starting position of each circle
        int starty = 0, startx = 0;
        // The number of traversals of Y-axis and X-axis in each circle
        int leny = sizey - 1, lenx = sizex - 1;
        vector<int> ans;
        // Single row matrix
        if(sizey == 1) {
            for(int x = startx, y = starty; x < startx + lenx + 1; x ++) {
                ans.emplace_back(matrix[y][x]);
            }
            return ans;
        }
        // Single column matrix
        if(sizex == 1) {
            for(int x = startx, y = starty; y < starty + leny + 1; y ++) {
                ans.emplace_back(matrix[y][x]);
            }
            return ans;
        }

        while(loop --) {
            for(int x = startx, y = starty; x < startx + lenx; x ++) {
                ans.emplace_back(matrix[y][x]);
            }
            for(int x = startx + lenx, y = starty; y < starty + leny; y ++) {
                ans.emplace_back(matrix[y][x]);
            }
            for(int x = startx + lenx, y = starty + leny; x > startx; x --) {
                ans.emplace_back(matrix[y][x]);
            }
            for(int x = startx, y = starty + leny; y > starty; y --) {
                ans.emplace_back(matrix[y][x]);
            }

            starty ++;
            startx ++;
            leny -= 2;
            lenx -= 2;
        }
        // The last circle is a line
        if(sizey <= sizex && sizey % 2 == 1) {
            for(int x = startx, y = starty; x < startx + lenx + 1; x ++) {
                ans.emplace_back(matrix[y][x]);
            }
        }
        // The last circle is a column
        if(sizey > sizex && sizex % 2 == 1) {
            for(int x = startx, y = starty; y < starty + leny + 1; y ++) {
                ans.emplace_back(matrix[y][x]);
            }
        }

        return ans;
    }
};

② Simulation

• The path of the spiral matrix can be simulated. The initial position is the upper left corner of the matrix, and the initial direction is to the right. When the path exceeds the limit or enters the previously accessed position, it rotates clockwise to enter the next direction.
• To determine whether the path enters the previously accessed location, an auxiliary matrix visited with the same size as the input matrix needs to be used, in which each element indicates whether the location has been accessed. When an element is accessed, set the element at the corresponding position in visited as accessed.
• How to determine whether the path ends? Since each element in the matrix is accessed once, the length of the path is the number of elements in the matrix. When the length of the path reaches the number of elements in the matrix, it is the complete path, and the path is returned.
• Java example:

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        boolean[][] visited = new boolean[rows][columns];
        int total = rows * columns;
        int row = 0, column = 0;
        int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order.add(matrix[row][column]);
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
}

• C + + example:

class Solution {
private:
    static constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return {};
        }
        
        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<bool>> visited(rows, vector<bool>(columns));
        int total = rows * columns;
        vector<int> order(total);

        int row = 0, column = 0;
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order[i] = matrix[row][column];
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
};

• Complexity analysis:
• • Time complexity: O(mn), where m and n are the number of rows and columns of the input matrix respectively. Each element in the matrix is accessed once.
• • Spatial complexity: O(mn). You need to create a size of m × n matrix visited records whether each location has been accessed.

③ Layer by layer simulation (LeetCode official solution)

• The matrix can be regarded as several layers, first outputting the outermost elements, then outputting the sub outer elements, until outputting the innermost elements.
• The k-th layer of the definition matrix is all vertices with a distance of K from the nearest boundary. For example, the outermost elements of the following matrix are layer 1, the sub outer elements are layer 2, and the remaining elements are layer 3:

[[1, 1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1, 1]]

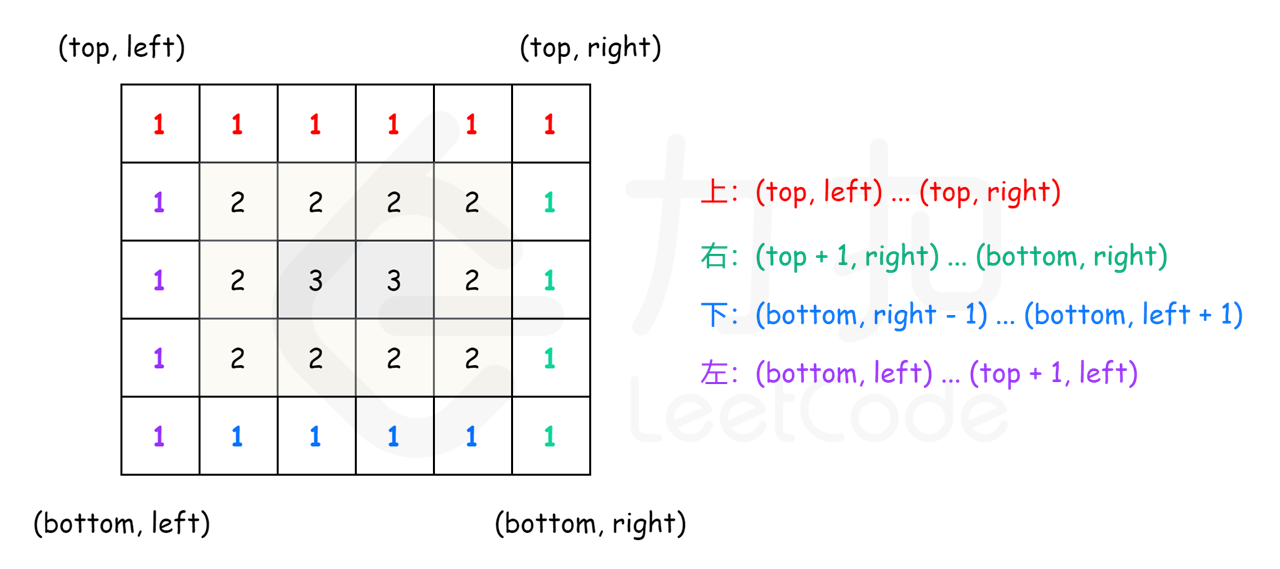
• For each layer, start at the top left and traverse all elements in clockwise order. Assuming that the upper left corner of the current layer is located at (top,left) and the lower right corner is located at (bottom,right), traverse the elements of the current layer in the following order.
• • Traverse the upper elements from left to right, from (top,left) to (top,right).
• • Traverse the right element from top to bottom, from (top+1,right) to (bottom,right).
• • If left < right and top < bottom, traverse the lower elements from right to left, from (bottom,right − 1) to (bottom,left+1), and from bottom to top, from (bottom,left) to (top+1,left).
• After traversing the elements of the current layer, increase left and top by 1 respectively, and decrease right and bottom by 1 respectively. Enter the next layer and continue traversing until all elements are traversed.

• Java example:

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

• C + + example:

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return {};
        }

        int rows = matrix.size(), columns = matrix[0].size();
        vector<int> order;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.push_back(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.push_back(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.push_back(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.push_back(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
};

3, Blog star

• This year is my first time to participate in the blog star. I need the support of all leaders. In my busy schedule, take some valuable time to vote for me: https://bbs.csdn.net/topics/603955258 Give me a five-star (the list will reply one by one). Thank you very much!