Primitive polynomial is a concept in modern algebra. It is a polynomial with the largest common factor of 1 satisfying all coefficients on the unique decomposition domain. The primitive polynomial is not equal to zero, and the polynomials associated with the primitive polynomial are still primitive polynomials;

1) In MATLAB, primitive polynomials can be generated by the function primely (x).
2) In MATLAB, a minimum primitive polynomial can be found through the function gfprimfd(m,'min').

The next resource of csdn is called "primitive polynomial c language generation";

Run up and have a look. You can generate and test whether it is primitive polynomial and inverse;

 

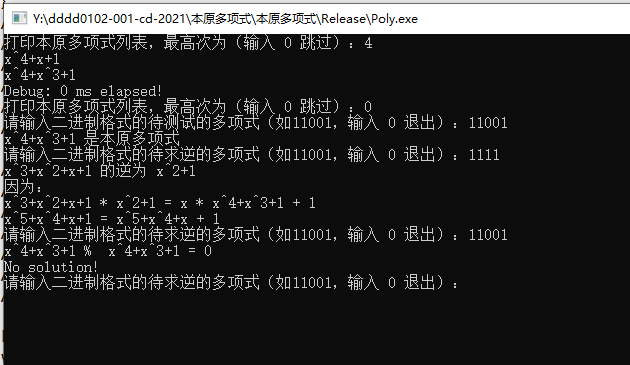
Create a new MFC single document project; Put poly H and poly CPP added to the project; Generate it; The following error appears;

Add "stdafx.h" to the corresponding file, and the error will disappear;

The error shown in the figure below appears again after the reconstruction;

 

Put "stdafx.h" before other header files,

 

The primitive polynomials listed when entering 7 are as follows,

 

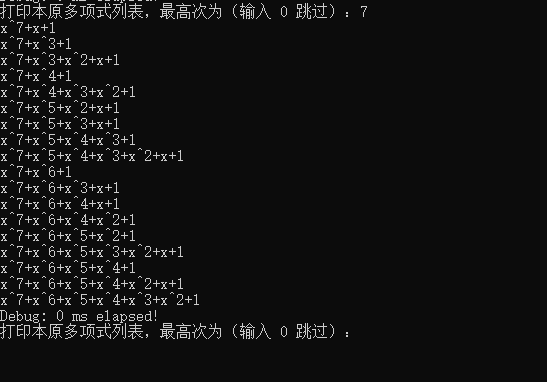
According to its original code, call the listPrimitive function of Poly class to pass a maximum number of terms, that is, output the original polynomial sequence; Next, 7 is passed, and the device description table handle is passed for output;

 

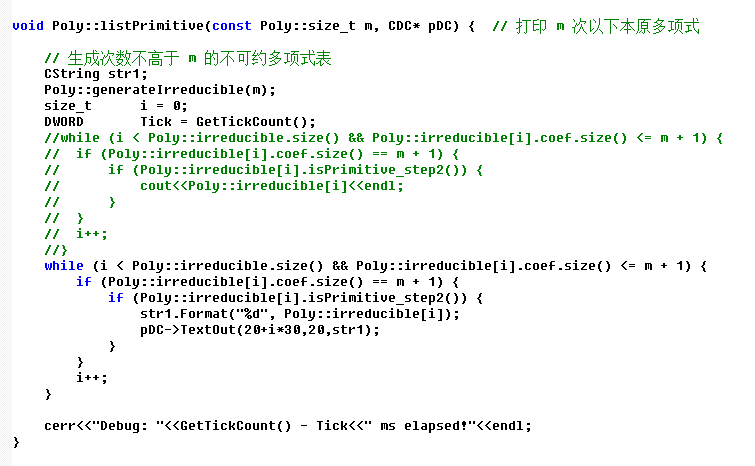
Its original function is as follows; This function has only one output statement of cout < < in C + +;

According to its original meaning, it is simply changed to PDC - > textout() output; The following figure;

 

Run it, just output a bunch of numbers; So how do polynomials output? It's x^4+x^3+1. How to output this?

 

Look at the code; The < < operator of C + + was overloaded; In this overload, the plus sign is output, and 1 or X or x ^ is output according to the situation; Is such an output polynomial;

 

Its original code; The generated polynomial is put into the vector;

void Poly::generateIrreducible(const Poly::size_t m) {
	// Generate irreducible polynomial table with degree not higher than m			

	Poly				f;	
	if (Poly::irreducible.empty()) {		
		Poly::irreducible.push_back(Poly("10"));
		Poly::irreducible.push_back(Poly("11"));
	}		
	// Skip computed irreducible polynomials
	f.coef.resize(Poly::irreducible[Poly::irreducible.size() - 1].coef.size(), 0);	
	f.coef.reserve(m + 1);
	f.coef.push_back(1);
	while (f.coef.size() <= (m + 1)) {		
		size_t				i;
		const size_t		size = f.coef.size();
		const size_t		max_exp = (size - 1) / 2;
		const size_t		list_size = Poly::irreducible.size();
		// In the division test, the divisor is not higher than max_ All irreducible polynomials of exp degree
		i = 0;
		while (i < list_size && Poly::irreducible[i].coef.size() <= max_exp + 1) {
			if ((f % Poly::irreducible[i]).isZero())
				break;
			i++;
		}
		if (i == list_size || Poly::irreducible[i].coef.size() > max_exp + 1) {
			// All irreducible polynomials are irreducible polynomials
			//cerr<<"Debug: irreducible "<<f<<endl;
			Poly::irreducible.push_back(f);
		}
		// Generate the next polynomial to be tested
		i = 0;
		while (i < size) {
			if (f.coef[i] == 0) {
				f.coef[i] = 1;
				break;
			} else {
				f.coef[i] = 0;
			}
			i++;
		}
		if (i == size) {
			f.coef.push_back(1);
		}
	}
	//for (size_t i = 0; i < Poly::irreducible.size(); i++) {	
	//	cerr<<"Debug: irreducible "<<Poly::irreducible[i]<<endl;
	//}
}

First understand its code; Transform listPrimitive,

void Poly::listPrimitive(const Poly::size_t m, CDC* pDC) {	// Print primitive polynomials below m times			

	// Generate irreducible polynomial table with degree not higher than m		
	CString str1;
	int row;
	Poly::generateIrreducible(m);
	size_t		i = 0;
	DWORD		Tick = GetTickCount();	
	//while (i < Poly::irreducible.size() && Poly::irreducible[i].coef.size() <= m + 1) {
	//	if (Poly::irreducible[i].coef.size() == m + 1) {
	//		if (Poly::irreducible[i].isPrimitive_step2()) {
	//			cout<<Poly::irreducible[i]<<endl;
	//		}
	//	}
	//	i++;
	//}
	row=0;
	while (i < Poly::irreducible.size() && Poly::irreducible[i].coef.size() <= m + 1) {
		if (Poly::irreducible[i].coef.size() == m + 1) {
			if (Poly::irreducible[i].isPrimitive_step2()) {
				str1.Format("%d", Poly::irreducible[i]);
				pDC->TextOut(20+i*10,20+row*i,str1);
				int			idx = 6;

				while (idx >= 0) {					
						if (idx == 0) {
							pDC->TextOut(20+i*30,20+row*i,"1");
						} else if (idx == 1) {
							pDC->TextOut(20+i*30,20+row*i,"x");
						} else {
							pDC->TextOut(20+i*30,20+row*i,"x^");
						}
					
					idx--;
				}
			}
		}
		i++;
	}	

	//cerr<<"Debug: "<<GetTickCount() - Tick<<" ms elapsed!"<<endl;
}

Take a look at the output; Unsuccessful,

Then idx should be the length of a single polynomial generated each time; So much first;  

The primitive polynomial is also used in the construction of spread spectrum code sequence of spread spectrum communication; At the same time, this paper is classified into the development category of communication software;