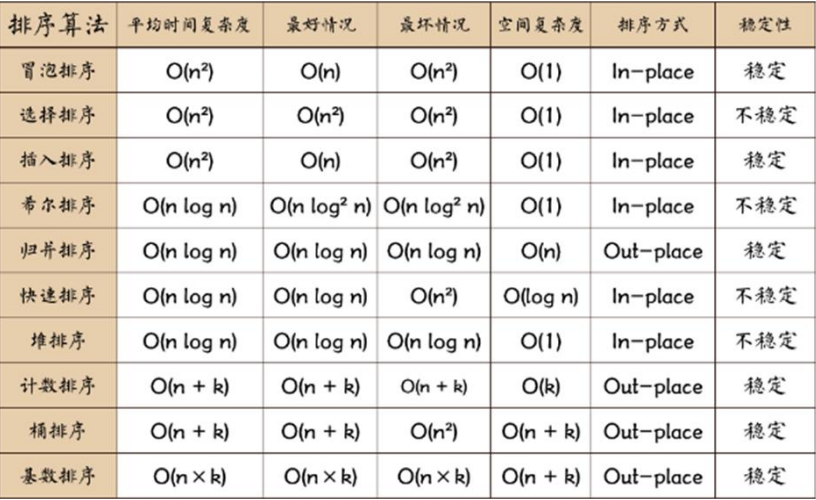
1. Bubble sorting
The basic idea of Bubble Sorting is to compare the values of adjacent elements from front to back (starting from the elements with smaller subscripts) through the sequence to be sorted, and exchange if the reverse order is found, so that the elements with larger values gradually move from front to back, just like bubbles under the water.
Because in the sorting process, each element is constantly close to its own position. If there is no exchange after a comparison, it indicates that the sequence is orderly. Therefore, a flag flag should be set in the sorting process to judge whether the elements have been exchanged. This reduces unnecessary comparisons. (the optimization mentioned here can be carried out after the bubble sort is written.)

Code implementation:
import java.text.SimpleDateFormat;
import java.util.Date;
public class BubbleSort {
public static void main(String[] args) {
// int[] arr={3,9,-1,10,20};
//
// System.out.println("array before sorting");
// System.out.println(Arrays.toString(arr));
//Test the bubble sorting speed O(n^2), give 80000 data, test
//Create a random array to give 80000
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String data1 = simpleDateFormat.format(new Date());
System.out.println("The time before sorting is" + data1);
//Bubble sorting
bubbleSort(arr);
SimpleDateFormat simpleDateFormat2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String data2 = simpleDateFormat.format(new Date());
System.out.println("The time before sorting is" + data2);
// System.out.println("sorted array");
// System.out.println(Arrays.toString(arr));
//The bubble sorting algorithm is encapsulated into a method
/*
//Define a temporary variable
int temp=0;
boolean flag=false;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j]>arr[j+1]){
flag=true;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if (!flag){
System.out.println("The sorted array is "");
System.out.println(Arrays.toString(arr));
break;
}else {
flag=false;
System.out.println("The "+ (i+1) +" array after sorting ");
System.out.println(Arrays.toString(arr));
}
}
*/
}
public static void bubbleSort(int[] arr){
//Define a temporary variable
int temp=0;
boolean flag=false;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j]>arr[j+1]){
flag=true;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if (!flag){
break;
}else {
flag=false;
}
}
}
}2. Select Sorting
Basic introduction
Selective sorting also belongs to the internal sorting method. It is to select an element from the data to be sorted according to the specified rules, and then exchange positions according to the regulations to achieve the purpose of sorting.
Select Sorting idea:
select sorting is also a simple sorting method. Its basic idea is: select the minimum value from arr[0]~arr[n-1] for the first time, exchange with arr[0], select the minimum value from arr[1]~arr[n-1], exchange with arr[1], select the minimum value from arr[2]~arr[n-1], exchange with arr[2],, select the minimum value from arr[i-1]~arr[n-1], exchange with arr[i-1], and select the minimum value from arr[n-2]~arr[n-1] for the n-1, Exchange with arr[n-2] for a total of n-1 times to obtain an ordered sequence arranged from small to large according to the sorting code.

Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class SelectSort {
public static void main(String[] args) {
/* int[] arr={101,34,119,1};
System.out.println("Before sorting ~ ");
System.out.println(Arrays.toString(arr));
//Select sort
selectSort(arr);
System.out.println("After sorting ~ ");
System.out.println(Arrays.toString(arr));
*/
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
String data1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println("Before sorting~");
System.out.println(data1);
//Select sort
selectSort(arr);
String data2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println("After sorting~");
System.out.println(data2);
}
public static void selectSort(int[] arr){
/* //first round
int minIndex=0;
int min=arr[0];
for (int i = 0+1; i < arr.length; i++) {
if (min>arr[i]){
minIndex=i;
min=arr[i];
}
}
if (minIndex!=0){
arr[minIndex]=arr[0];
arr[0]=min;
}
System.out.println("After the first round ~ ");
System.out.println(Arrays.toString(arr));
//Second round
minIndex=1;
min=arr[1];
for (int i = 1+1; i < arr.length; i++) {
if (min>arr[i]){
minIndex=i;
min=arr[i];
}
}
if (minIndex!=1){
arr[minIndex]=arr[1];
arr[1]=min;
}
System.out.println("After the second round ~ ");
System.out.println(Arrays.toString(arr));
//Third round
minIndex=2;
min=arr[2];
for (int i = 2+1; i < arr.length; i++) {
if (min>arr[i]){
minIndex=i;
min=arr[i];
}
}
if (minIndex!=2){
arr[minIndex]=arr[2];
arr[2]=min;
}
System.out.println("After the third round ~ ");
System.out.println(Arrays.toString(arr));
*/
for (int i = 0; i < arr.length-1; i++) {
int minIndex=i;
int min=arr[i];
for (int j = i+1; j < arr.length; j++) {
if (min>arr[j]){
min=arr[j];
minIndex=j;
}
}
if (minIndex!=i){
arr[minIndex]=arr[i];
arr[i]=min;
}
}
}
}3. Insert sort
Plug in sorting belongs to internal sorting method, which is to find the appropriate position of the element to be sorted by inserting, so as to achieve the purpose of sorting.
Idea of Insertion Sorting: the basic idea of Insertion Sorting is to treat n elements to be sorted as an ordered table and an unordered table. At the beginning, the ordered table contains only one element, and the unordered table contains n-1 elements. In the sorting process, the first element is taken out of the unordered table every time, Compare its sort code with the sort code of the elements of the ordered table in turn, and insert it into the appropriate position in the ordered table to make it a new ordered table.
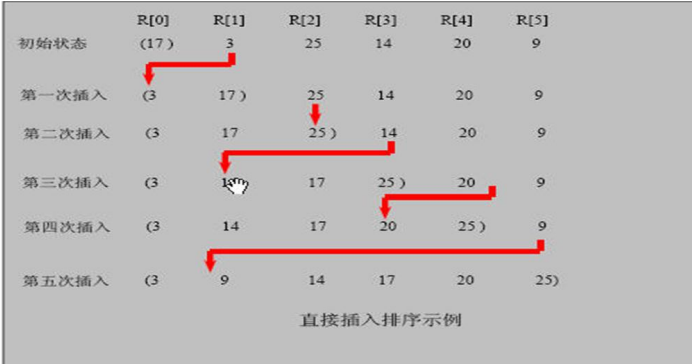
Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class InsertSort {
public static void main(String[] args) {
/* int[] arr={101,34,119,1,-1,89};
System.out.println("Before sorting ~ ");
System.out.println(Arrays.toString(arr));
//Insert sort
insertSort(arr);
System.out.println("After sorting ~ ");
System.out.println(Arrays.toString(arr));
*/
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
String data1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println("Before sorting~");
System.out.println(data1);
//Select sort
insertSort(arr);
String data2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println("After sorting~");
System.out.println(data2);
}
public static void insertSort(int[] arr){
/* //First round insertion
int insertVal=arr[1];
int insertIndex=1-1;
while (insertIndex>=0&&insertVal<arr[insertIndex]){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1]=insertVal;
System.out.println("Insert ~ ") in the first round;
System.out.println(Arrays.toString(arr));
//Second round insertion
insertVal=arr[2];
insertIndex=2-1;
while (insertIndex>=0&&insertVal<arr[insertIndex]){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1]=insertVal;
System.out.println("Insert ~ ") in the second round;
System.out.println(Arrays.toString(arr));
//Third round insertion
insertVal=arr[3];
insertIndex=3-1;
while (insertIndex>=0&&insertVal<arr[insertIndex]){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1]=insertVal;
System.out.println("Insert ~ ") in the third round;
System.out.println(Arrays.toString(arr));
*/
for (int i = 0; i < arr.length-1; i++) {
int insertVal=arr[i+1];
int insertIndex=i;
while (insertIndex>=0&&insertVal<arr[insertIndex]){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
if (insertIndex!=i){
arr[insertIndex+1]=insertVal;
}
}
}
}4. Hill sort
Introduction to Hill ranking method
Hill sorting is a sort algorithm proposed by Donald Shell in 1959. Hill sort is also an insert sort. It is an improved version of simple insert sort, also known as reduced incremental sort.
Basic idea of Hill ranking method
Hill sort is to group records by certain increment of subscript, and sort each group by direct insertion sort algorithm; As the increment decreases, each group contains more and more keywords. When the increment decreases to 1, the whole file is just divided into one group, and the algorithm terminates.
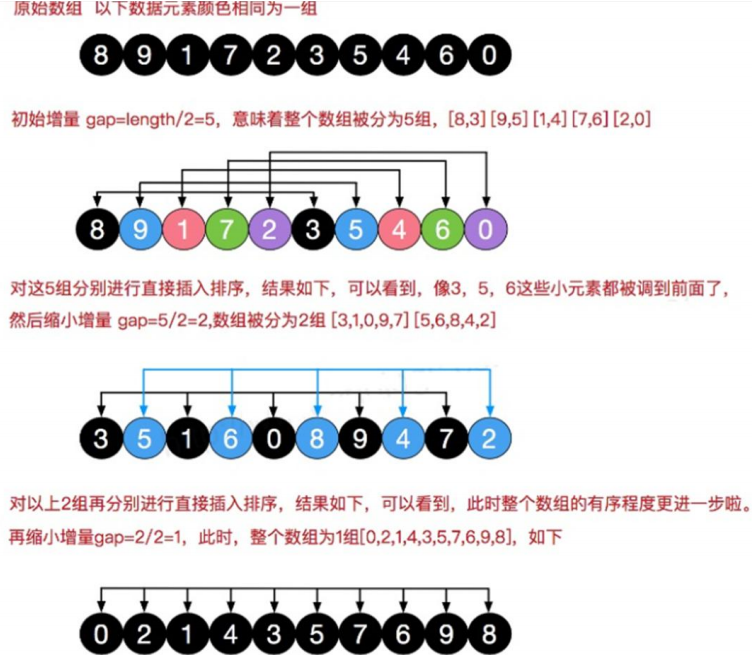
Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class ShellSort {
public static void main(String[] args) {
// int[] arr={8,9,1,7,2,3,5,4,6,0};
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
System.out.println("Before sorting");
// System.out.println(Arrays.toString(arr));
String date1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date1);
//Hill sort exchange
// shellSort(arr);
//Hill sort shift
shellSort2(arr);
System.out.println("After sorting");
// System.out.println(Arrays.toString(arr));
String date2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date2);
}
//Hill sort exchange method
public static void shellSort(int[] arr){
/*
//first round
int temp=0;
for (int i=5;i< arr.length;i++){
for (int j=i-5;j>=0;j-=5){
if (arr[j]>arr[j+5]){
temp=arr[j];
arr[j]=arr[j+5];
arr[j+5]=temp;
}
}
}
System.out.println("After the first round of hill sorting = "+ Arrays.toString(arr));
//Second round
temp=0;
for (int i=2;i< arr.length;i++){
for (int j=i-2;j>=0;j-=2){
if (arr[j]>arr[j+2]){
temp=arr[j];
arr[j]=arr[j+2];
arr[j+2]=temp;
}
}
}
System.out.println("After the second round of hill sorting = "+ Arrays.toString(arr));
//Third round
temp=0;
for (int i=1;i< arr.length;i++){
for (int j=i-1;j>=0;j-=1){
if (arr[j]>arr[j+1]){
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println("After the third round of hill sorting = "+ Arrays.toString(arr));
*/
int temp=0;
for (int gap= arr.length/2;gap>0;gap/=2){
for (int i = gap; i < arr.length; i++) {
for (int j=i-gap;j>=0;j-=gap){
if (arr[j]>arr[j+gap]){
temp=arr[j];
arr[j]=arr[j+gap];
arr[j+gap]=temp;
}
}
}
}
}
//Hill sort shift method
public static void shellSort2(int[] arr){
//Increment gap and gradually reduce the increment
for (int gap= arr.length/2;gap>0;gap/=2){
for (int i = gap; i < arr.length; i++) {
int j=i;
int temp=arr[j];
if (arr[j]<arr[j-gap]){
while (j-gap>=0&&temp<arr[j-gap]){
//move
arr[j]=arr[j-gap];
j-=gap;
}
//When the while is pushed out, find the insertion location for temp
arr[j]=temp;
}
}
}
}
}5. Quick sort
Introduction to quick sort method:
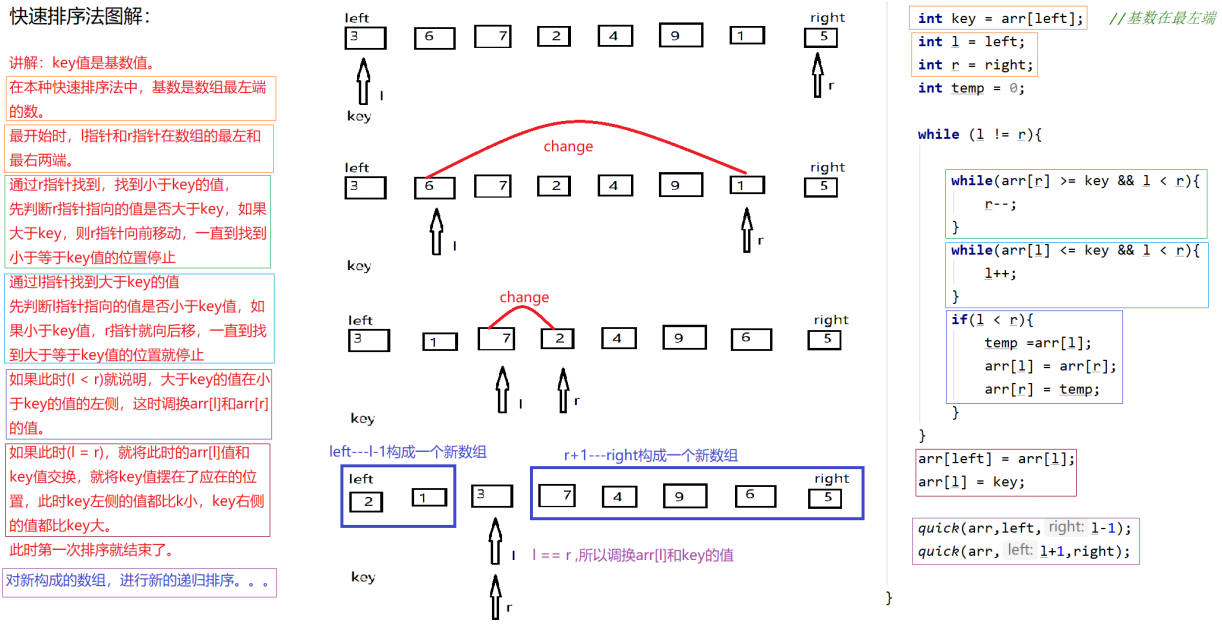
Quicksort is an improvement on bubble sort. The basic idea is: divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be carried out recursively, so as to turn the whole data into an ordered sequence
Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class QuickSort {
public static void main(String[] args) {
// int[] arr={-9,78,0,23,-567,70};
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
System.out.println("Before sorting");
// System.out.println(Arrays.toString(arr));
String date1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date1);
//Quick sort
quickSort(arr,0, arr.length-1);
System.out.println("After sorting");
// System.out.println(Arrays.toString(arr));
String date2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date2);
}
public static void quickSort(int[] arr,int left,int right){
if (arr==null||arr.length==0){
return;
}
if (left>right){
return;
}
int key=arr[left];//The cardinality is at the leftmost end
int l=left;
int r=right;
int temp=0;
while (l!=r){
while (arr[r]>=key&&l<r){
r--;
}
while (arr[l]<=key&&l<r){
l++;
}
if (l<r){
temp=arr[l];
arr[l]=arr[r];
arr[r]=temp;
}
}
arr[left]=arr[l];
arr[l]=key;
quickSort(arr,left,r-1);
quickSort(arr,l+1,right);
}
}

6. Merge and sort
Introduction to merging and sorting:
Merge sort is a sort method based on the idea of merging. The algorithm adopts the classical divide and conquer strategy (divide and conquer divides the problem into some small problems and then solves them recursively, while the conquer stage "fixes" the answers obtained in the stages, that is, divide and conquer).
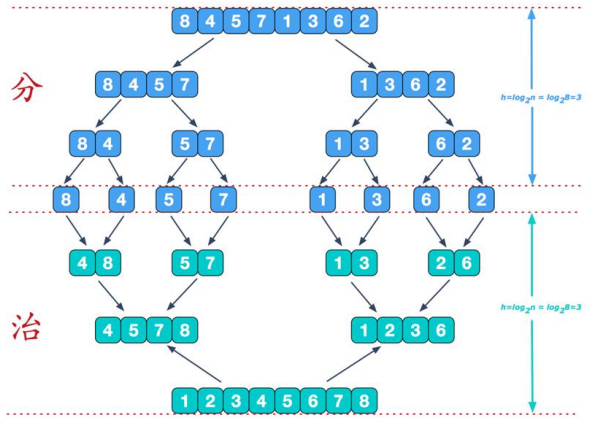
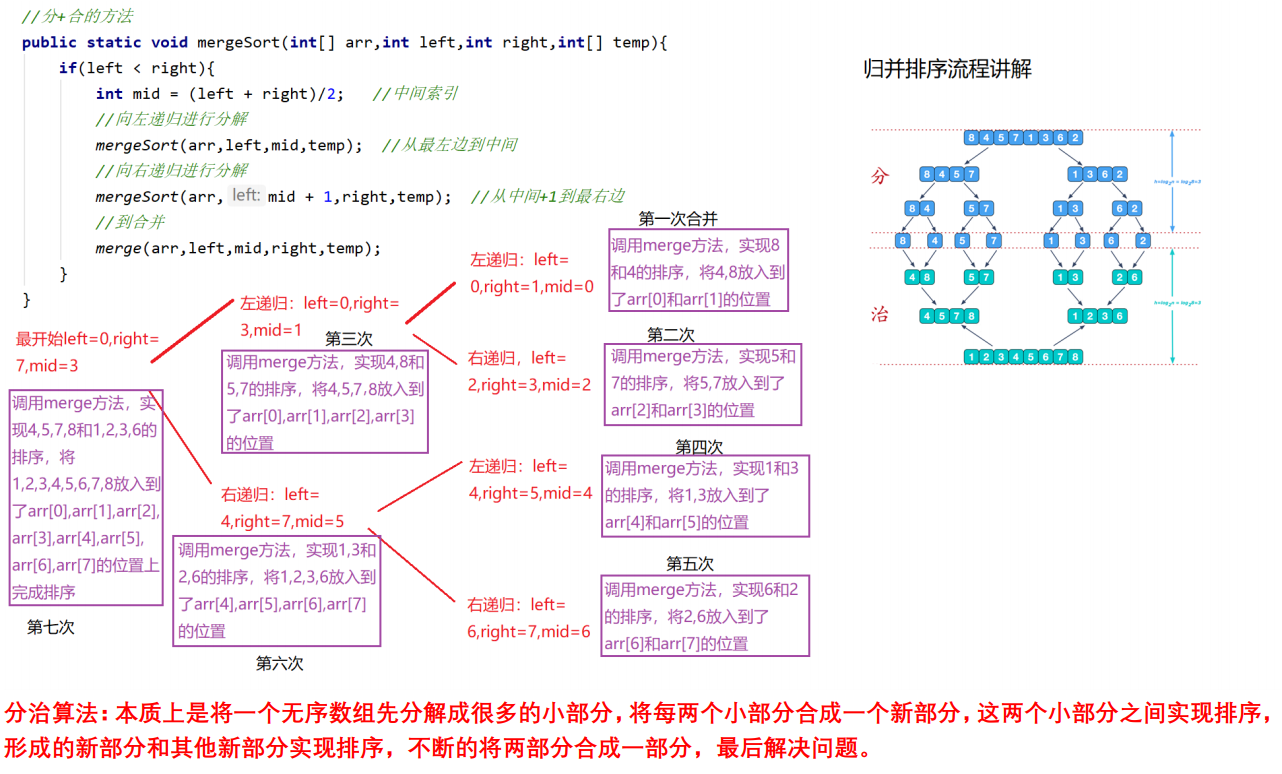
Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class MergeSort {
public static void main(String[] args) {
// int[] arr={8,4,5,7,1,3,6,2};
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
int[] temp=new int[arr.length];
System.out.println("Before sorting!");
String date1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date1);
//Merge sort
mergeSort(arr,0, arr.length-1, temp);
System.out.println("After sorting!");
String date2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date2);
}
//Sub + sum method
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if (left<right){
int mid=(left+right)/2;//Intermediate index
//Decompose recursively to the left
mergeSort(arr,left,mid,temp);
//Decompose recursively to the right
mergeSort(arr,mid+1,right,temp);
//merge
merge(arr,left,mid,right,temp);
}
}
//Merging method
/**
*
* @param arr Sorted original array
* @param left Initial index of left ordered sequence
* @param mid Intermediate index
* @param right Right index
* @param temp Array for transit
*/
public static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i=left;//Initialization i, the initial index of the left ordered sequence
int j=mid+1;//Initialization j, the initial index of the ordered sequence on the right
int t=0;//Points to the current index of the temp array
//(I)
// First, fill the left and right (ordered) data into the temp array according to the rules
// Until one side of the ordered sequence on the left and right is processed
while (i<=mid&&j<=right){
//If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
//Fill the current element on the left into the temp array
//Then t++,i++
if (arr[i]<=arr[j]){
temp[t]=arr[i];
t++;
i++;
}else {//On the contrary, fill the current element of the ordered sequence on the right into the temp array
temp[t]=arr[j];
t++;
j++;
}
}
//(II)
//Fill all the data on the side with remaining data into temp in turn
while (i<=mid){//The ordered sequence on the left and the remaining elements are filled into temp
temp[t]=arr[i];
t++;
i++;
}
while (j<=right){//The ordered sequence on the right and the remaining elements are filled into temp
temp[t]=arr[j];
t++;
j++;
}
//(III)
//Copy the elements of temp array to arr
//Note that not all are copied every time
t=0;
int tempLeft=left;
while (tempLeft<=right){
arr[tempLeft]=temp[t];
t++;
tempLeft++;
}
}
}7. Cardinality sorting
Basic idea of cardinality sorting
1) Unify all values to be compared into the same digit length, and fill zero in front of the shorter digit. Then, start from the lowest order and sort once in turn. In this way, the sequence becomes an ordered sequence from the lowest order to the highest order.
2) This explanation is difficult to understand. Let's take a graphic explanation to understand the steps of cardinality sorting
Cardinality sorting graphic description
Sort the array {53,3542748,14214} in ascending order using cardinality

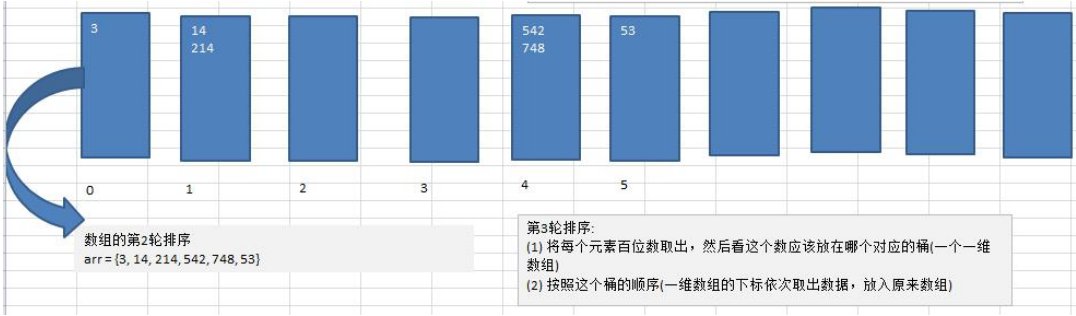
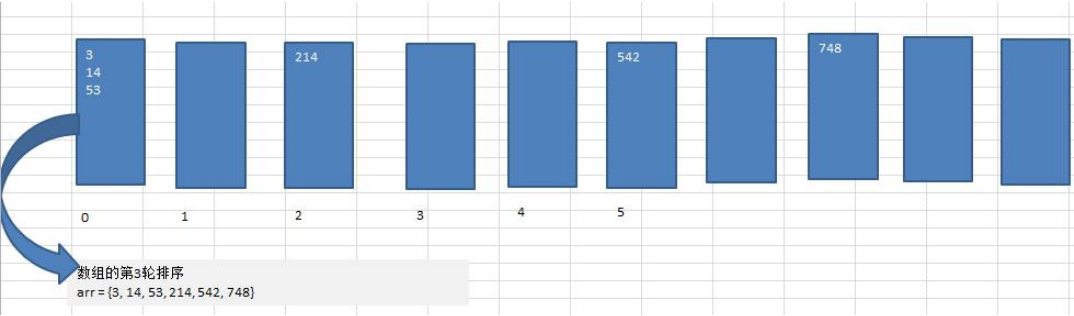
Code implementation:
import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class RadixSort {
public static void main(String[] args) {
// int[] arr={53,3,542,748,14,214};
int[] arr=new int[80000];
for (int i = 0; i < 80000; i++) {
arr[i]= (int) (Math.random()*80000);
}
System.out.println("Before sorting");
// System.out.println(Arrays.toString(arr));
String date1 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date1);
//Cardinality sort
radixSort(arr);
System.out.println("After sorting");
// System.out.println(Arrays.toString(arr));
String date2 = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
System.out.println(date2);
}
public static void radixSort(int arr[]){
int max=arr[0];
for (int i = 1; i < arr.length; i++) {
if (max<arr[i]){
max=arr[i];
}
}
int maxLength = (max + "").length();
int bucket[][]=new int[10][arr.length];
int bucketElementCount[]=new int[10];
for (int i = 0,n=1; i < maxLength; i++,n*=10) {
for (int j = 0; j < arr.length; j++) {
int digitOfElement=arr[j]/n%10;
bucket[digitOfElement][bucketElementCount[digitOfElement]]=arr[j];
bucketElementCount[digitOfElement]++;
}
int index=0;
for (int k = 0; k < bucket.length; k++) {
if (bucketElementCount[k]!=0){
for (int l = 0; l < bucketElementCount[k]; l++) {
arr[index]=bucket[k][l];
index++;
}
}
bucketElementCount[k]=0;
}
}
/*
//first round
for (int i = 0; i < arr.length; i++) {
//Take out the value of one bit of each element
int digitOfElement=arr[i]%10;
//Put it into the corresponding bucket
bucket[digitOfElement][bucketElementCount[digitOfElement]]=arr[i];
bucketElementCount[digitOfElement]++;
}
//According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
int index=0;
//Traverse each bucket, and put the data in the bucket into the original array
for (int k = 0; k < bucket.length; k++) {
//If there is data in the bucket, we put it into the original array
if (bucketElementCount[k]!=0){
//Loop the bucket, i.e. the k-th bucket (i.e. the k-th one-dimensional array), and put it into
for (int l = 0; l < bucketElementCount[k]; l++) {
//Take out the element and put it into the arr
arr[index]=bucket[k][l];
index++;
}
}
//After the 1st round of processing, each bucket e l ementcounts [k] = 0!!!!
bucketElementCount[k]=0;
}
System.out.println("First round sorting arr = "+ arrays. ToString (ARR));
//Second round
for (int i = 0; i < arr.length; i++) {
int digitOfElement=arr[i]/10%10;
bucket[digitOfElement][bucketElementCount[digitOfElement]]=arr[i];
bucketElementCount[digitOfElement]++;
}
index=0;
for (int k = 0; k < bucket.length; k++) {
if (bucketElementCount[k]!=0){
for (int l = 0; l < bucketElementCount[k]; l++) {
arr[index]=bucket[k][l];
index++;
}
}
bucketElementCount[k]=0;
}
System.out.println("The second round of sorting arr = "+ arrays. ToString (ARR));
//Third round
for (int i = 0; i < arr.length; i++) {
int digitOfElement=arr[i]/100%10;
bucket[digitOfElement][bucketElementCount[digitOfElement]]=arr[i];
bucketElementCount[digitOfElement]++;
}
index=0;
for (int k = 0; k < bucket.length; k++) {
if (bucketElementCount[k]!=0){
for (int l = 0; l < bucketElementCount[k]; l++) {
arr[index]=bucket[k][l];
index++;
}
}
bucketElementCount[k]=0;
}
System.out.println("The third round of sorting arr = "+ arrays. ToString (ARR));
*/
}
}
8. Sorting method summary