reference material

1. Ten classic sorting algorithm animation and analysis, look at me! (complete version with code)
2. https://www.bilibili.com/video/BV1Kb411W75N
3. Merge sort
4. Merging sorting of graphic sorting algorithm (4)

0. Basic concepts

1. Sorting: it is an important operation in computer programming. Its function is to rearrange a set or sequence of data elements into an orderly sequence according to the value of a data item of the data element.
2. Sort code (key): the data item by which to sort.
3. Stable sorting: maintain a consistent sorting method based on the positional relationship between the same key elements before and after sorting.
4. Unstable sorting: a sorting method in which the relative position of the same key elements changes before and after sorting
5. Sorting is divided into two categories:
   1. Internal sort: refers to the sort in which the sequence to be sorted is completely stored in memory. Internal sort can be roughly divided into five categories: insert sort, exchange sort, selection sort, merge sort and allocation sort.
   2. External sort: refers to the sort that needs to access external memory during the sorting process.

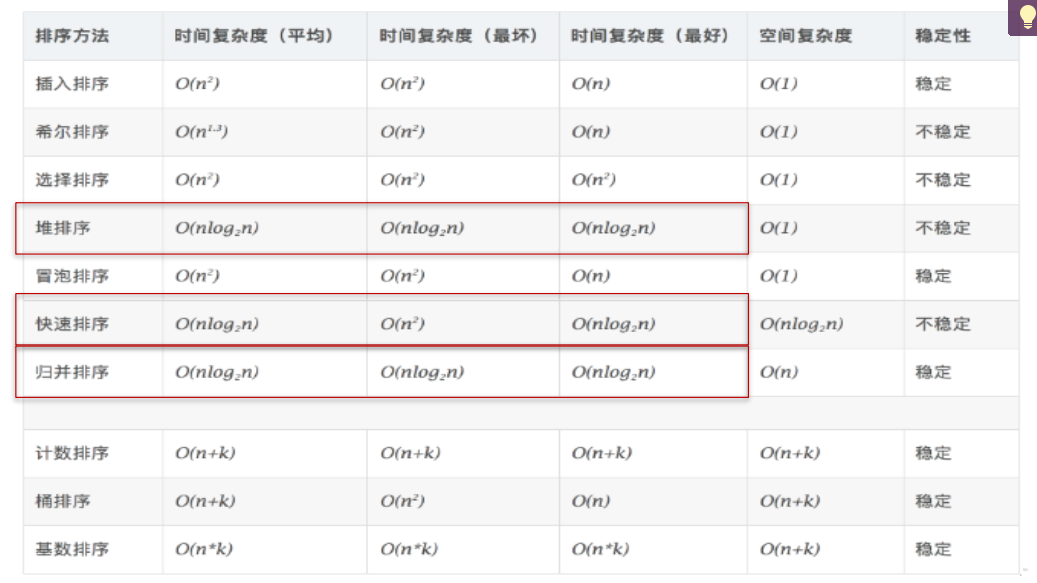
Comparison of ten classical sorting algorithms

1. Insert sort

• basic thought
  Insert an element to be sorted into the appropriate position of the previously ordered sub file according to the size of its keyword until all records are inserted.

1.1 direct insertion sort

1.1.1 basic idea

The n elements to be sorted are regarded as an ordered table and an unordered table. At the beginning, the ordered table contains only one element, and the unordered table contains n-1 elements. In the sorting process, the first element is taken out from the unordered table every time, its sorting code is compared with the sorting code of the elements of the ordered table, and it is inserted into the appropriate position in the ordered table to make it a new ordered table.

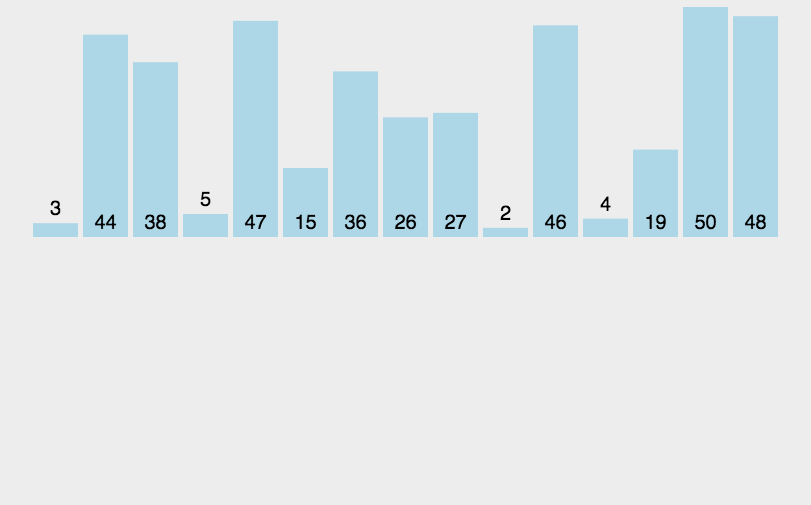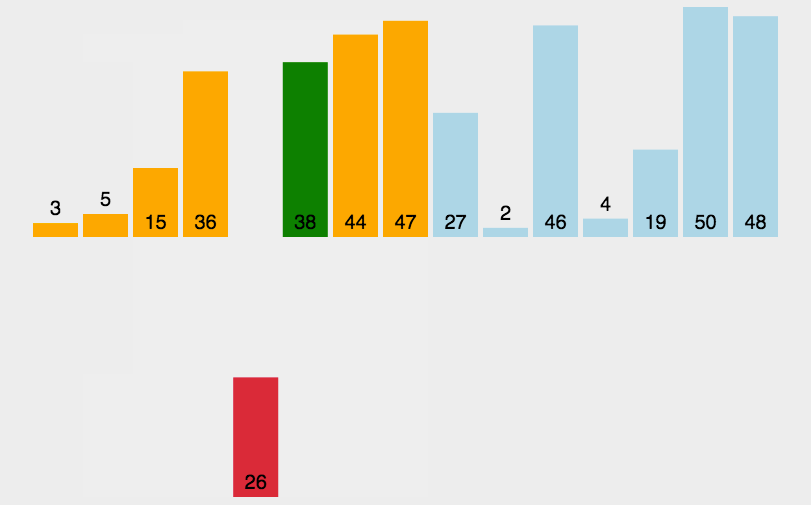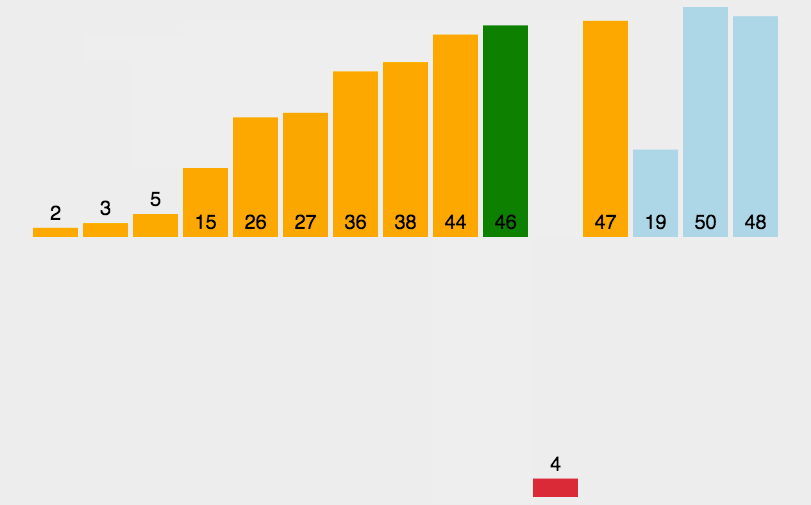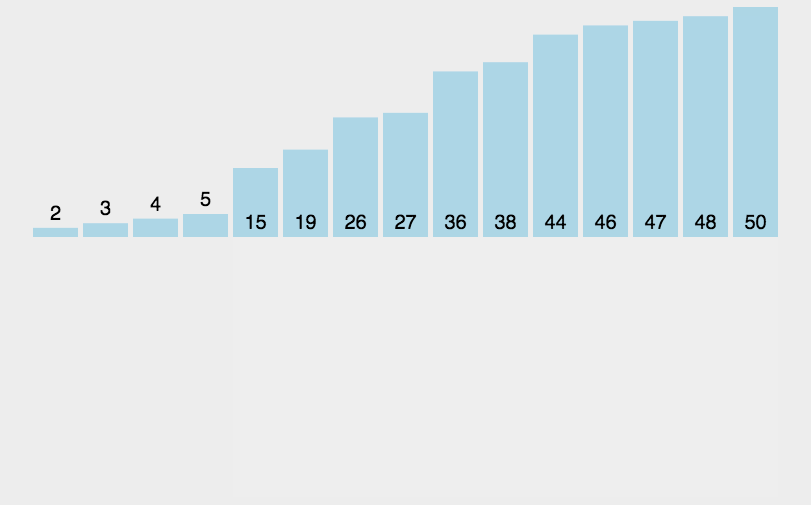
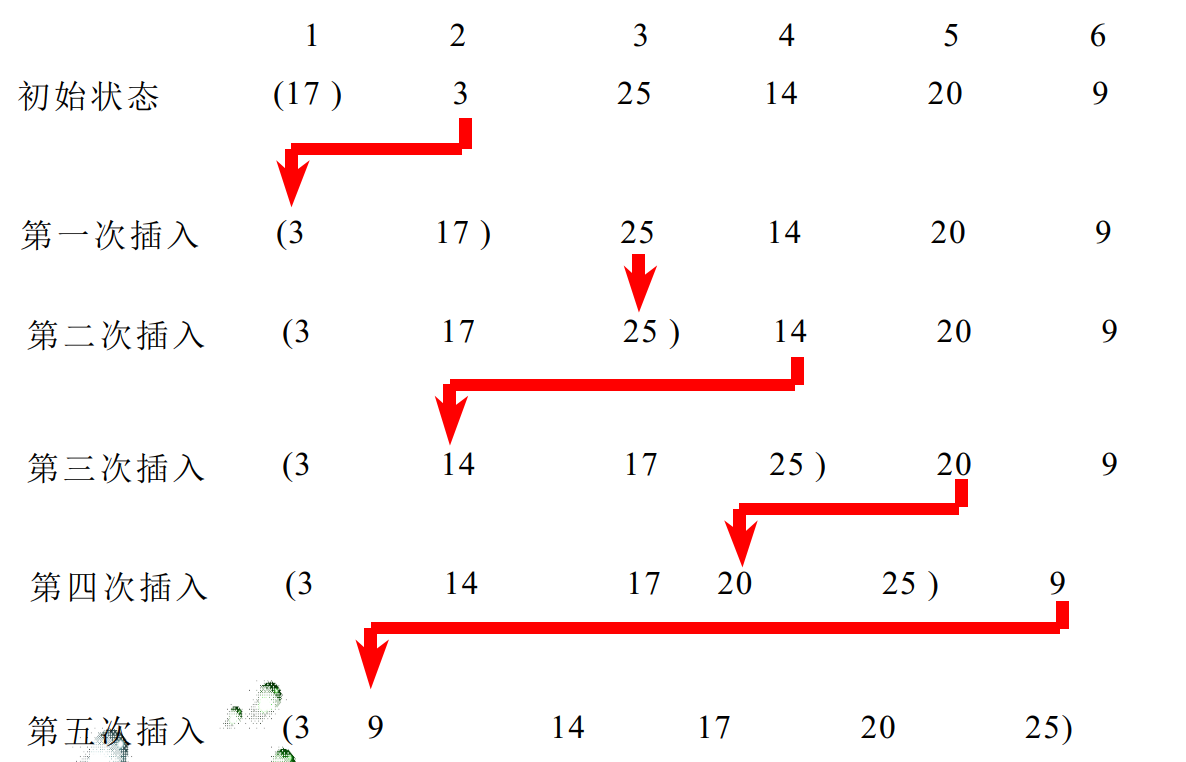
• For example, n=6, the six sorting codes of array R are: [17, 3, 25, 14, 20, 9], and the execution process of direct insertion sorting is as follows:
  

package pers.chh3213.sort;

import java.util.Arrays;

/**
* DirectInsertSort.java
* @Description Direct insertion method
* @author chh3213
* @version
* @date 2021 11:19:07 am, December 26
 */
public class DirectInsertSort {
	public static void main(String[] args) {
		DirectInsertSort insertSort = new DirectInsertSort();
		int[] arr = {9, -16, 310, 23, -30, -49, 25, 21, 30};
		insertSort.directInsertSort(arr);
		System.out.println(Arrays.toString(arr));
	}
	public void directInsertSort(int[] arr) {
		// FA Yi
		for (int i = 1; i < arr.length; i++) {
				int temp = arr[i];           // Record the data to insert
				int j=i;
				for ( ; j>0&&arr[j-1]>temp; j--) {// Compare from the rightmost of the sorted sequence to find a smaller number
					arr[j]=arr[j-1];
				}
				if(j!=i)arr[j]=temp;	
		}
		//Method II
//		for (int i = 1; i < arr.length; i++) {
//			for(int j=i;j>0;j--) {
//				if(arr[j]<arr[j-1])swap(arr, j, j-1);
//			}
//		}
	}
	public void swap(int[] arr, int i, int j) {
		int temp =arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}


}

1.1.2 efficiency analysis of direct insertion sorting

• First, from the perspective of space, it only needs the auxiliary space of one element for the position exchange of elements. From the time analysis, firstly, the outer loop should be inserted n-1 times, each insertion should be compared at least once (positive sequence) and moved 0 times; Compare i times at most (including the comparison with temp), and move i+1 times (in reverse order) (i=2,3,..., n). Therefore, the time complexity of direct insertion sorting is O ( n 2 ) O(n^2) O(n2) .
• The element movement of direct insertion sorting is sequential, and the method is stable.

1.2 Hill sort (reduced incremental sort)

1.2.1 basic idea

First, divide the whole sequence of elements to be arranged into several subsequences (composed of elements separated by a certain increment) for direct insertion sorting. When the elements in the whole sequence are basically in order (the increment is small enough), then carry out a direct insertion sorting for all elements. Because the efficiency of direct insertion sorting is very high when the elements are basically ordered (close to the best case), Hill sorting has a great improvement in time efficiency.

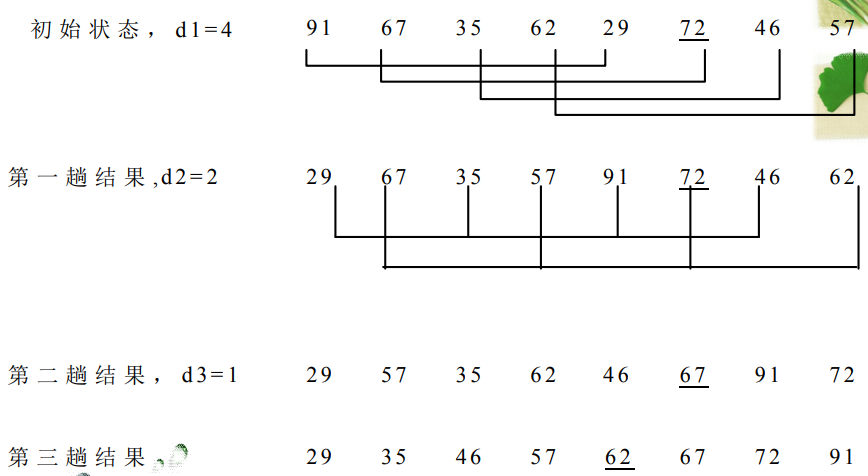
• For example, the key codes of 8 elements are 91, 67, 35, 62, 29, 72, 46 and 57 respectively. The execution process of hill sorting algorithm is as follows:

d1=8/2=4;
d2=4/2=2;
d3=2/2=1;

• step

  1. Select an incremental sequence t1, t2,..., tk, where ti > TJ, tk = 1;

  2. According to the number of incremental sequences k, the sequences are sorted by k times of direct insertion;

  3. For each sorting, the sequence to be sorted is divided into several subsequences with length m according to the corresponding increment ti, and each sub table is directly inserted and sorted. Only when the increment factor is 1, the whole sequence is treated as a table, and the table length is the length of the whole sequence.

package pers.chh3213.sort;

import java.util.Arrays;

public class ShellSort {
	public static void main(String[] args) {
		ShellSort shell = new ShellSort();
		int[] arr = {9, -16, 310, 23, -30, -49, 25, 21, 30};
		shell.shellSort(arr);
		System.out.println(Arrays.toString(arr));
	}
	public void shellSort(int[] arr) {
		//The first step length is array length / 2, followed by step length / 2
		for (int step = arr.length /2; step >0; step /= 2) {
			//Direct insert sort
			for (int i = step; i < arr.length; i++) {
				int temp = arr[i];//The first number of the right to be sorted area
				int j=i-step;//Index of the first number of sorted areas on the left
				for( ;j>=0&&arr[j]>temp;j-=step) {
					arr[j+step]=arr[j];//If the conditions are met, move the sorted number back one position
//					swap(arr, j, j+step);
				}
				//Insert the number to be sorted to the specified position
				arr[j+step]=temp;
			}


		}
	}
	public void swap(int[] arr, int i, int j) {
		int temp =arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}
}

1.2.2 efficiency analysis of hill sorting

• Although our algorithm is a three-layer loop, the outermost loop is l o g 2 ( n ) log_2(n) In the order of log2 (n), the for loop in the middle is of the order of N, and the inner loop is much lower than the order of N, because when there are more groups, there are fewer elements in the group, and the number of cycles is less; When there are fewer groups, the elements in the group increase, but they are close to order, and the number of cycles does not increase. Therefore, the time complexity of hill sorting is O ( n l o g 2 n ) O(nlog_2n) O(nlog2# n) and O ( n 2 ) O(n^2) Between O(n2), approximately O ( n 1.3 ) O(n^{1.3}) O(n1.3) .
• Because Hill sort compares each subsequence separately, when comparing
  It is possible to change the original sequence of elements with the same sort code by moving elements
  So Hill sort is unstable.

2. Exchange sorting

• It is mainly through the comparison of the key codes of two records in the sorting table. If they are weaker than the reverse of the sorting requirements (do not meet the ascending or descending order), they will be exchanged.

2.1 bubble sort

2.1.1 basic idea

Bubble sorting compares two elements at a time by repeatedly visiting the sequence to be sorted, and swaps them if they are in the wrong order.

• Principle description
  By comparing the sorting codes of adjacent elements from the front to the back of the sequence to be sorted, if the reverse order is found, it will be exchanged, so that the elements with larger sorting codes will gradually move from the front to the rear.

• Implementation steps (in ascending order by default)

  1. Compare adjacent elements. If the former is larger than the latter, exchange the two numbers;
  2. Repeat the above steps for all elements except the last one until no pair of numbers need to exchange positions.

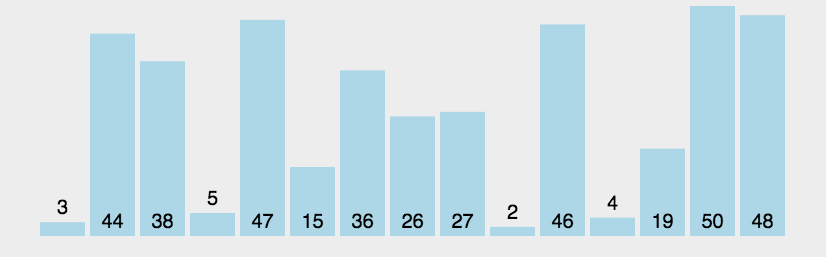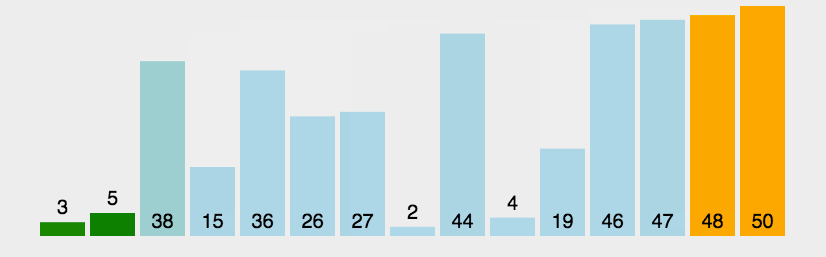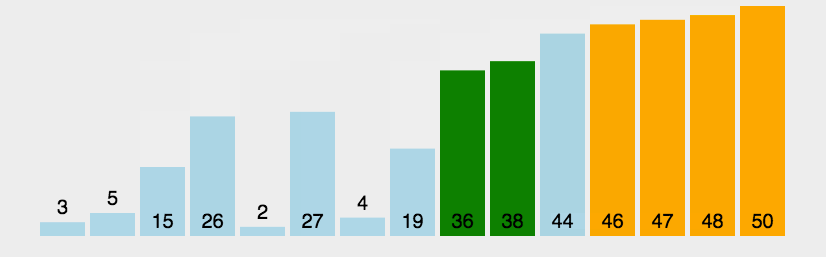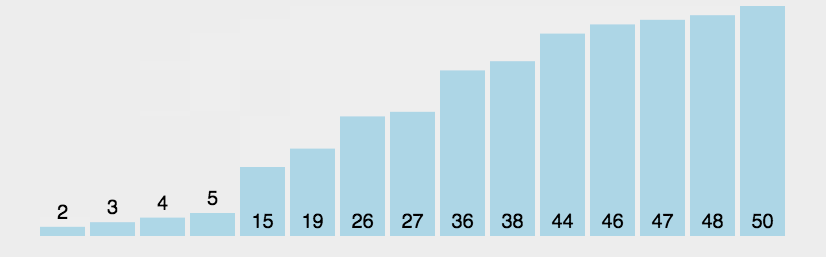
• Example

package pers.chh3213.sort;
import java.util.Iterator;
import java.util.Scanner;
public class BubbleSort {
	public static void main(String[] args) {
		int[] arr = {5,4,1,966,2,3,56,89,12,0,56562};
		System.out.println("before sort:");
		for (int i : arr) {
			System.out.print(i+"\t");
		}
		for (int i = 0; i < arr.length-1; i++) {
			for (int j = 0; j < arr.length-1-i; j++) {
				if(arr[j]>arr[j+1]) {
					int temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
		System.out.println();
		System.out.println("after sort:");
		for (int i : arr) {
			System.out.print(i+"\t");
		}
	}
}

Because in the sorting process, each element is constantly approaching its own position. If there is no exchange after a comparison, it indicates that the sequence is orderly. Therefore, a flag swap can be set in the sorting process to judge whether the elements have been exchanged, so as to reduce unnecessary comparison. The improvement code is as follows:

	public void bubbleSort(int[] data) {
		for (int i = 0; i < data.length-1; i++) {
			boolean swap = false;
			for (int j = 0; j < data.length-i-1; j++) {
				if(data[j]>data[j+1]) {
					int temp = data[j];
					data[j]= data[j+1];
					data[j+1] = temp;
					swap = true;
				}
			}
			if(!swap)break; //Stop sorting when not swapping
		}
	}

2.1.2 efficiency analysis of bubble sorting

• It can be seen from the bubble sorting algorithm that if the elements to be sorted are in positive order, only one sorting is required, the number of comparisons is (n-1) times, and the number of moving elements is 0; If the elements to be sorted are in reverse order, n-1 times of sorting is required, and the comparison times are ( n 2 − n ) / 2 (n^2-n)/2 (n2 − n)/2, the number of moves is 3 ( n 2 − n ) / 2 3(n^2-n )/2 3(n2 − n)/2, so the time complexity of bubble sorting algorithm is O ( n 2 ) O(n^2) O(n2) . Because the elements move more, it belongs to the slower one in internal sorting. Because the bubble sorting algorithm only moves the order between elements, it is a stable algorithm.

2.2 quick sort

• Invented by Tony Hoare, a Turing prize winner, it is listed as one of the top ten algorithms in the 20th century and the fastest of all internal sorting algorithms so far. Bubble sort upgrade, a kind of exchange sort. The time complexity of quick sort is O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n)).
• Fast platoon adopts the idea of divide and conquer.

2.2.1 sorting idea

1. Picking out an element from a sequence is called a benchmark( pivot)，Generally take the first element;
2. Through one division, the elements to be arranged are divided into left and right sub sequences. All elements smaller than the benchmark value are placed in the left sequence, and all elements larger than the benchmark value are placed in the right sequence (the same number can be on either side). After the partition, the benchmark is in the middle of the sequence. This is called**partition**(partition)Operation;
3. Then the two subsequences are divided until each sequence has only one element;
4. The final sequence is an ordered sequence.

(Note: picture source: Reference 1)

• Specific process of primary division

  1. low points to the first element of the area to be divided (index=0), and high points to the tail element of the area to be divided (index=R.length-1);
  2. base=R[low] (in order to reduce the movement of data, the standard elements are temporarily stored in the temporary variable base, and finally placed in the final position);
  3. High moves from back to front until R [high] < base;
  4. R[low]=R[high], low++;
  5. Move low from front to back until R [low] > = base;
  6. R[high]=R[low], high–;
  7. goto 3;
  8. Until low==high, R[low]=base (that is, put the standard element in its final position).

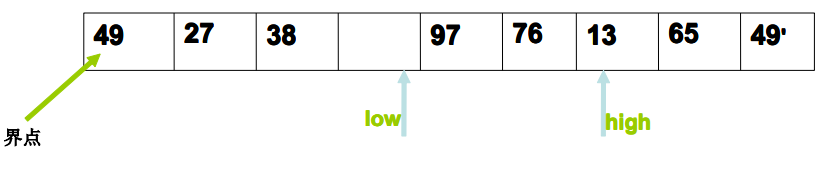
  Generally speaking, a partition is to scan from both ends of the table to the middle alternately, put the small one on the left and the large one on the right, and put it in the middle as a standard element.
  Then, the first half and the second half are sorted recursively. When the current half and the second half are ordered, the array will be naturally ordered.

• Specific process example of primary division

  1. low points to the first element of the area to be divided, and high points to the tail element of the area to be divided;
     
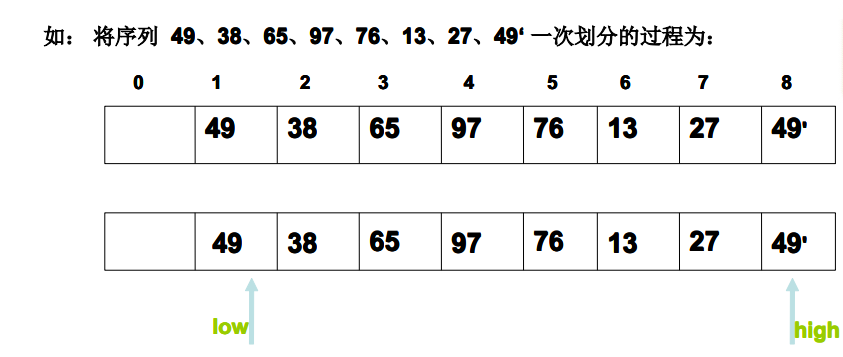
  2. R[0]=R[low] (in order to reduce the movement of data, the standard elements are temporarily stored in R[0], and finally placed in the final position);
     
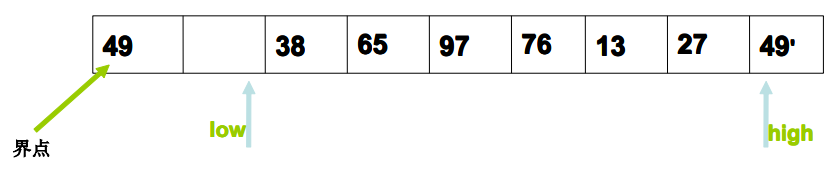
  3. High move from back to front until R [high] key<R[0]. key;
     
  4. R[low]=R[high], low++;

1. Move low from front to back until R [low] key>=R[0]. key;
   
2. R[high]=R[low], high–;
   
3. goto 3;

8. Until low==high, R[low]=R[0] (i.e. put the standard element in its final position).
-Example

package pers.chh3213.sort;
public class QuickSort {
	public static void main(String[] args) {
		System.out.println("quick sort test");
		int[] arr = {9, -16, 30, 23, -30, -49, 25, 21, 30};
		System.out.println("before sort:");
		for (int i : arr) {
			System.out.print(i+"\t");
		}
		QuickSort quick = new QuickSort();
		quick.quickSort(arr, 0, arr.length-1);
		System.out.println();
		System.out.println("after sort:");
		for (int i : arr) {
			System.out.print(i+"\t");
		}

	}
	public  void quickSort(int[] arr,int start, int end) {
		if(start<end) {
			 int index = partition(arr, start, end); //Divide Table 1 into 2
			 quickSort(arr, start, index-1); // Quick sorting of left subsequence
			 quickSort(arr, index+1, end); //Quick sorting of right subsequences
		}

	}
//	Primary division
	public  int partition(int[] arr, int low,int high) {

		int base = arr[low]; //Temporary base element to base
		while (low<high) {//Scan alternately from both ends of the table to the middle
			while(low<high && arr[high]>=base)high--;//Right end scan
			if(low<high) {
				arr[low]=arr[high];//Put elements smaller than the benchmark in front of the benchmark
				low++;
			}
			while(low<high && arr[low]< base)low++;//Left end scan
			if(low<high) {
				arr[high]=arr[low];//Put elements larger than the benchmark behind the benchmark
				high--;
			}
		}
		arr[low] = base;//Put the datum element in the final position

		return low;//Returns the location of the base element
	}
}

2.2.2 recursive tree for quick sorting

• The recursive process of quick sorting can be vividly given by a binary tree. The following figure shows the binary tree of the quick sort recursive calling process corresponding to the sequence to be arranged 4,38,65,97,76,13,27,49 (referred to as the quick sort recursive tree for short).
  

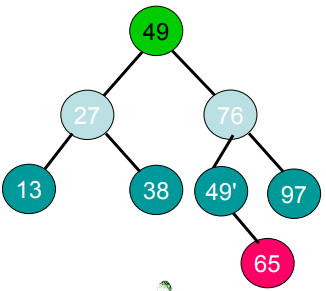
• From the recursive tree of the quick sort algorithm, the number of times of quick sort depends on the height of the recursive tree.

2.2.3 time complexity of quick sort

• If an object is located after each division, the left subsequence and right subsequence of the object
  If the length of the sequence is the same, the next step will be to sort the two subsequences whose length is halved, which is the most ideal case.

• Suppose n is a power of 2, n = 2 k , ( k = l o g 2 n ) n=2^k,(k=log_2n) n=2k,(k=log2  n), assuming that the reference position is in the middle of the sequence, the size of the divided sub intervals is basically the same.
  n + 2 ( n / 2 ) + 4 ( n / 4 ) + . . . + n ( n / n ) = n + n + . . . + n = n ∗ k = n ∗ l o g 2 n n+2(n/2)+4(n/4)+ ...+n(n/n)=n+n+ ...+n=n*k=n*log_2n n+2(n/2)+4(n/4)+...+n(n/n)=n+n+...+n=n∗k=n∗log2​n

• Therefore, the best time complexity for quick sorting is O ( n l o g 2 n ) O(nlog_2n) O(nlog2​n) . Moreover, it has been proved theoretically that the average time complexity of quick sorting is also O ( n l o g 2 n ) O ( nlog_2n) O(nlog2​n) . The experimental results show that fast sorting is the best of all internal sorting methods in terms of average computing time.

• In the worst case, that is, when the sequence of objects to be sorted has been sorted from small to large according to its sorting code, its recursive tree becomes a single tree, and each division only obtains a sub sequence of one object less than the last time (degenerated into bubble sorting). All objects can be located only after n-1 times, and the i-th time requires n-i sorting code comparison to find the placement position of the i-th object, and the total number of sorting code comparison will reach
  ∑ i = 1 n − 1 ( n − i ) = 1 2 n ( n − 1 ) ≈ n 2 2 \sum_{i=1}^{n-1}{(n-i)}=\frac{1}{2}n(n-1) \approx \frac{n^2}{2} ∑i=1n−1​(n−i)=21​n(n−1)≈2n2​
  Therefore, the worst time complexity of quick sort is O ( n 2 ) O(n^2) O(n2).

2.2.4 spatial complexity and stability of quick sort

• Quick sort is recursive, and a stack is needed to store pointers and parameters of recursive calls at each layer. The maximum number of recursive calls is consistent with the height of the recursive tree. Ideally l o g 2 ( n + 1 ) log_2(n+1) log2​(n+1)； In the worst case, that is, when the sequence of objects to be sorted has been sorted from small to large according to its sorting code, the recursive tree becomes a single tree with a depth of n. Therefore, the best spatial complexity of quick sorting is O ( l o g 2 n ) O (log_2n) O(log2 n), the worst spatial complexity is O ( n ) O(n) O (n) (i.e. auxiliary space required for quick sorting).
• Quick sort is an unstable sort method.

3. Select Sorting

• Basic principle: the elements to be sorted are divided into sorted (initially empty) and unordered groups, and the element with the smallest value in the unordered element is placed in the sorted group in turn.

3.1 simple selection sorting

3.1.1 basic process

1. Select the element with the smallest key from a set of elements R[i] to R[n]
2. If it is not the first element in the group, it is swapped with the first element in the group.
3. Remove the element with the smallest keyword and
   Repeat steps 1 and 2 in the element until there is only one remaining element.

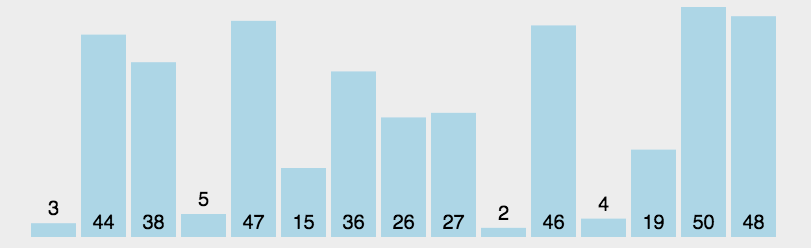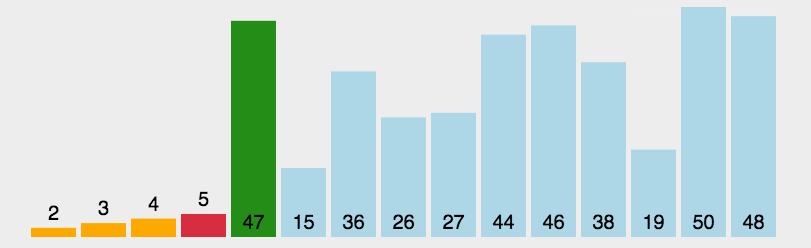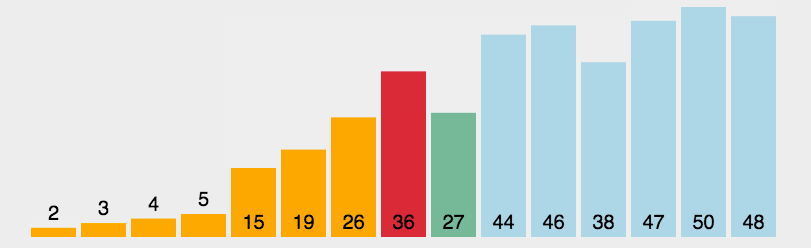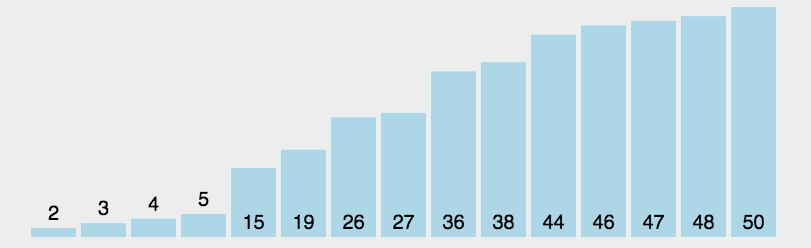
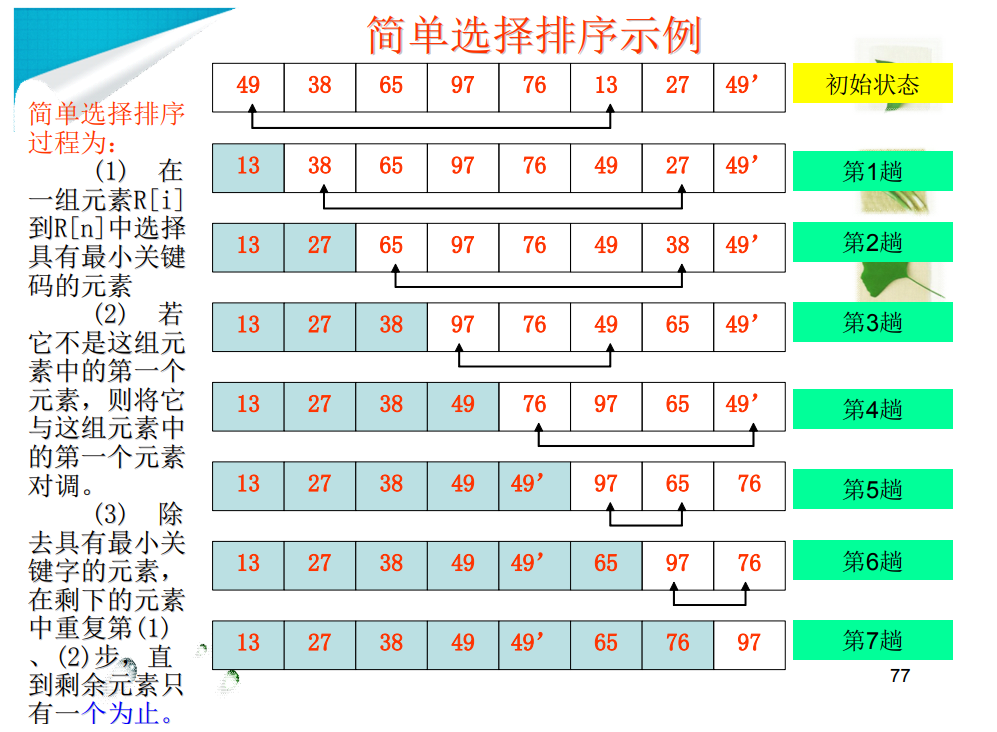
package pers.chh3213.sort;

import java.util.Arrays;

public class SelectSort {
	public static void main(String[] args) {
		SelectSort select = new SelectSort();
		int[] arr = {9, -16, 310, 23, -30, -49, 25, 21, 30};
		select.selectSort(arr);
		System.out.println(Arrays.toString(arr));
	}
	public void selectSort(int[] arr) {
		for (int i = 0; i < arr.length; i++) {//Sort n-1 times
			int min = i;
			for (int j = i+1; j < arr.length; j++) {
				if(arr[min]>arr[j])min=j; // Record the subscript of the lowest value element that can be found so far
			}
			 // After finding the minimum value, exchange the found minimum value with the value at i position
			if(i!=min)swap(arr, i, min);
		}
	}
	public void swap(int[] arr, int i, int j) {
		int temp =arr[i];
		arr[i]=arr[j];
		arr[j]=temp;
	}
}

3.1.2 efficiency analysis of simple selection sorting

1. Regardless of the initial state, n-i comparisons are required to select the element with the smallest key in the i-th sorting. Therefore, the total number of comparisons is:
   ∑ i = 1 n − 1 n − i = n ( n − 1 ) / 2 = O ( n 2 ) \sum_{i=1}^{n-1}{n-i}=n(n-1)/2=O(n^2) Σ i=1n − 1 − n − i=n(n − 1) / 2 = O (N2) (i.e. time complexity)

2. Best case: when the sequence is positive, the number of moves is 0 0 0, worst case: when the sequence is in reverse order, the exchange operation shall be performed for each sequence, and the total number of moves shall be the maximum 3 ( n − 1 ) 3(n-1) 3(n−1).

3. Because of the exchange between non adjacent elements in direct selection sorting, direct selection sorting is an unstable sorting method. For example, given a sorting code of 3, 7, 3 ', 2, 1, the sorted result is 1, 2, 3', 3, 7

3.2 heap sorting

• Heap sorting is an improvement on simple selection sorting. Selecting the record with the smallest keyword value from n records by direct selection sorting requires n-1 comparisons, and then selecting the smallest from the remaining n-1 records requires n-2 comparisons. Obviously, some comparisons in the two adjacent trips are repeated. In order to avoid repeated comparisons, tree selection sorting comparison can be used.
• Tree Selection Sort The total number of comparisons is O ( n l o g 2 n ) O(nlog2 n) O(nlog2n), which reduces the number of comparisons compared with direct selection sorting, but requires additional storage space to store intermediate comparison results and sorting results. Therefore, heap sorting is introduced.

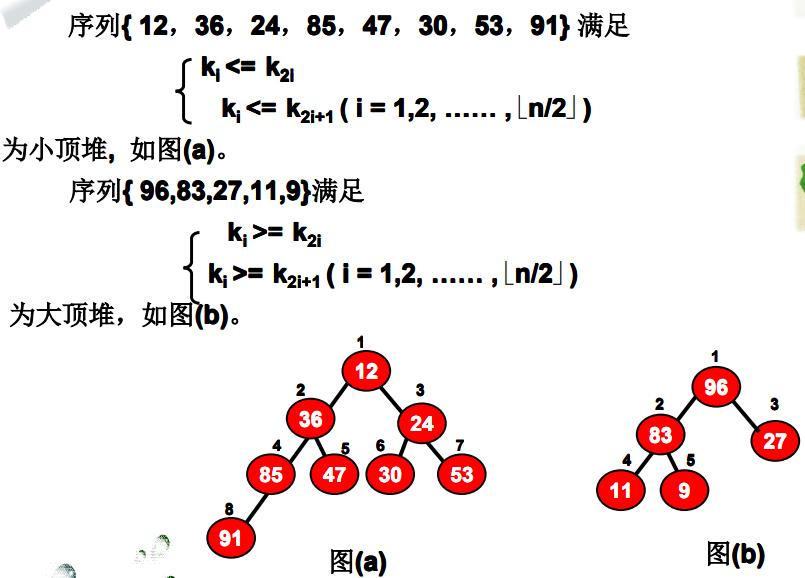
3.2.1 definition of reactor

• The sequence {K1, K2,..., kn} of n elements if and only if
  { k i ≤ k 2 i k i ≤ k 2 i + 1 (1) \begin{cases} k_i\le k_{2i} \\ k_i \le k_{2i+1} \tag{1} \end{cases} {ki​≤k2i​ki​≤k2i+1​​(1)
  perhaps
  { k i ≥ k 2 i k i ≥ k 2 i + 1 (1) \begin{cases} k_i\ge k_{2i} \\ k_i \ge k_{2i+1} \tag{1} \end{cases} {ki​≥k2i​ki​≥k2i+1​​(1)
  It's called a heap.

• If this sort code forms a complete binary tree in order, then (1) it is called small top heap (all node values of the binary tree are less than or equal to the values of the left and right children), and (2) it is called * * large top heap (* * all node values of the binary tree are greater than or equal to the values of the left and right children)

• Examples of small and large top piles
  

3.2.2 basic idea of heap sorting

1. Build initial reactor
   Sort codes K1, K2, K, Kn is expressed as a complete binary tree, and then it is filtered from the n/2 sorting code (i.e. the last non terminal node of the tree), so that the sub binary tree composed of this node as the root node meets the definition of heap, and then repeat the operation from the n/2-1 sorting code until the first sorting code. At this time, the binary tree conforms to the definition of heap, and the initial heap has been established.

2. Heap sort
   Exchange the data of the first node (binary tree root node) and the last node in the heap (k1, and kn,), and then k 1 k_1 k1​~ k n − 1 k_{n-1} kn − 1, rebuild the reactor, and then k1, and K_ The {n-2} exchange is repeated, and the number of elements to rebuild the heap each time is continuously reduced by 1 until there is only one element to rebuild the heap. When the heap sorting has been completed, the sorting code k 1 , k 2 , k 3 , . . , k n k1, k2, k3, .., kn k1,k2,k3,..,kn has been arranged in an ordered sequence.

3. Two steps of heap sorting

   • The initial heap is formed according to the initial input data
   • Sort through a series of element exchanges and readjustment of the heap.

4. Key problems of heap sorting

   • How to build a heap from an unordered sequence?
   • How do we adjust the remaining elements after the top elements of the output stack to make it a new heap?

4. Two way merge sort

4.1 basic ideas

• Merge two ordered tables into one ordered table.
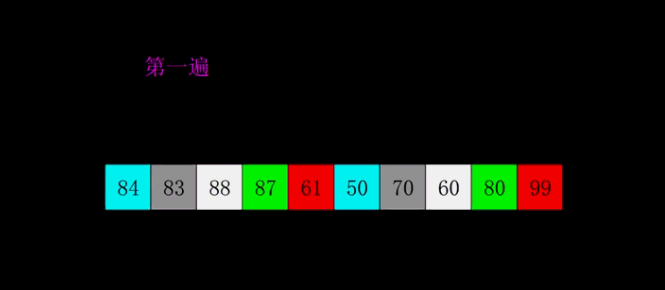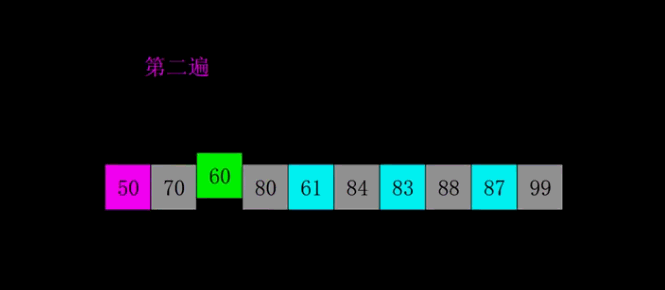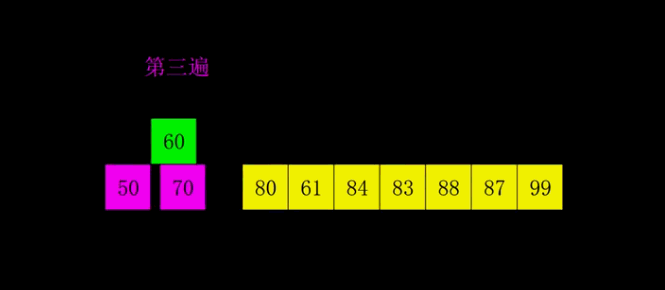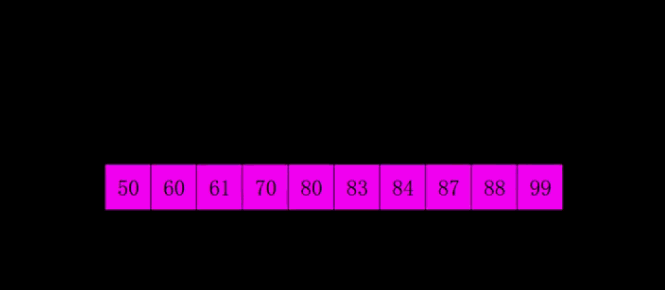
  For example, merge the following two sorted sequential tables into one sorted table. Compare the corresponding elements of the two in order, and move the smaller one into the other table. Repeat this until any one of the tables is moved into the other table.

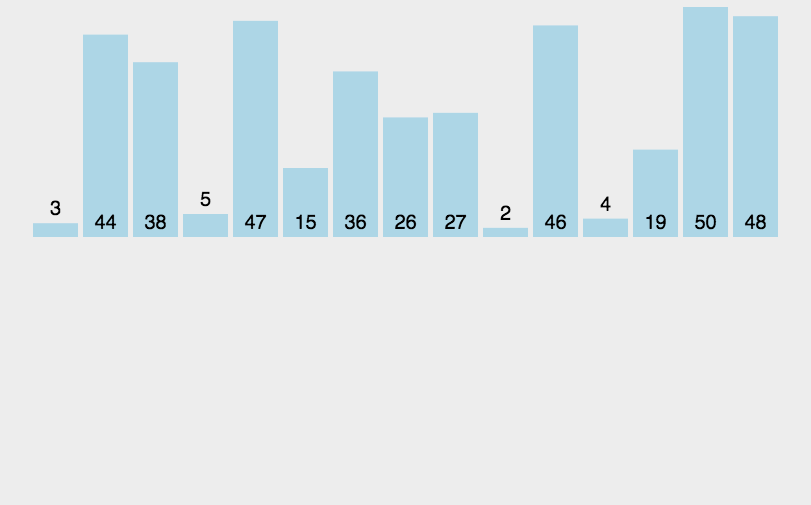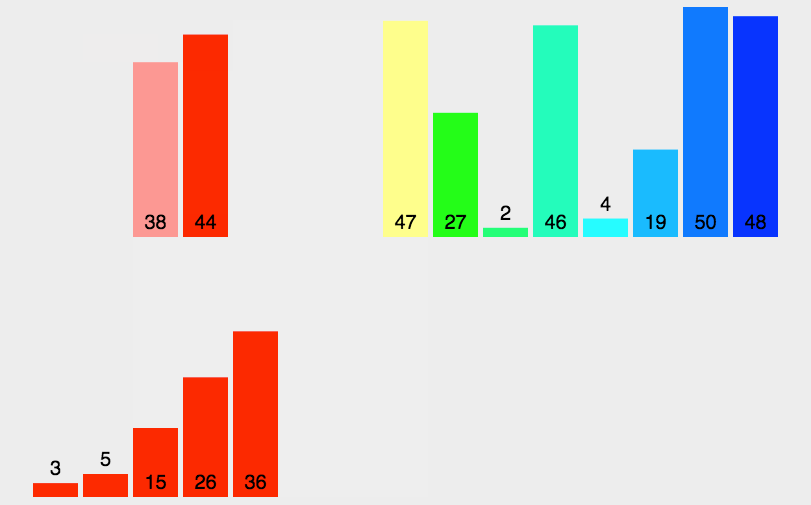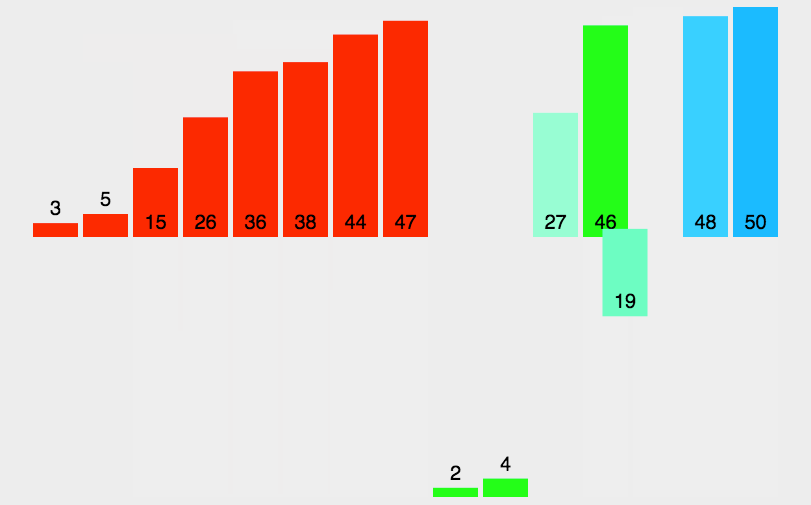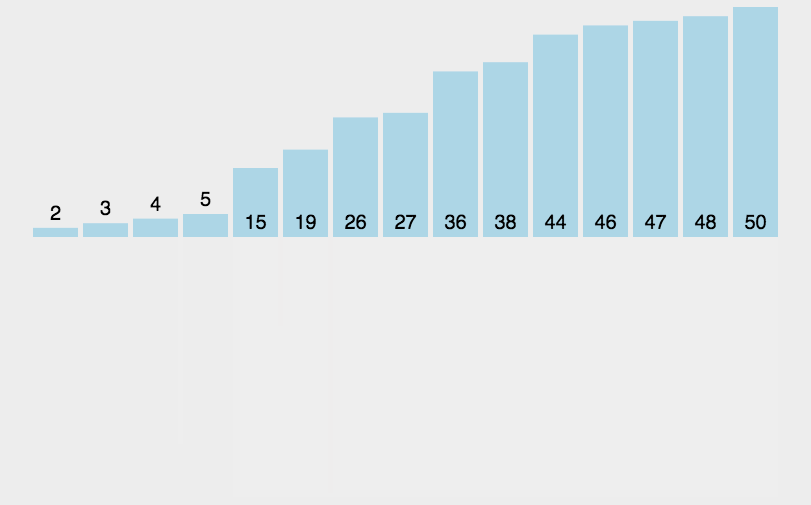
• Example
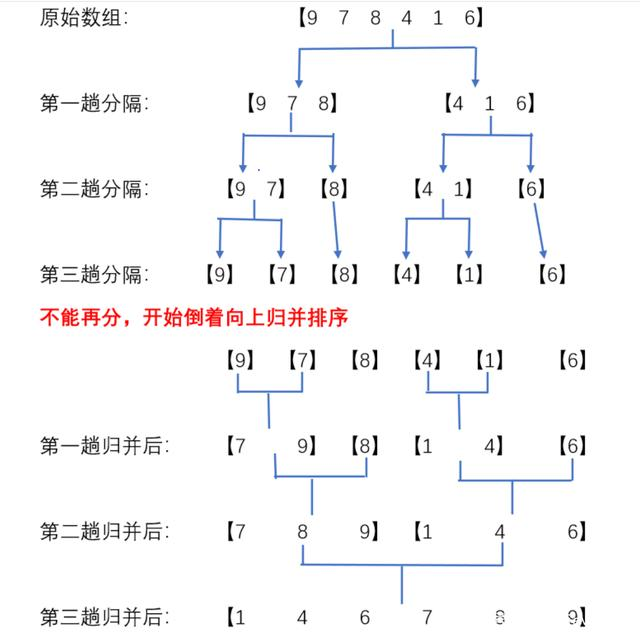  (picture source: Reference 3)

• characteristic

  1. In the process of "delivery", the array is equally divided into two, and then the sub array is divided into two;
  2. In the process of "return", the two ordered sub arrays are combined into an ordered sub array;

package pers.chh3213.sort;

import java.util.Arrays;
/**
 *
* MergeSort.java
* @Description Merge sort
* @author chh3213
* @version
* @date 2021 December 26, 2014 4:54:53 PM
 */
public class MergeSort {
	public static void main(String[] args) {
		MergeSort Sort = new MergeSort();
		int[] arr = {9, -16, 310, 23, -30, -49, 25, 21, 30};
		Sort.mergeSort(arr,0,arr.length-1);
		System.out.println(Arrays.toString(arr));
	}
	public void mergeSort(int[] arr,int left, int right) {
		int mid = (left+right)/2;
		if(left<right) {
			//recursion
			mergeSort(arr, left, mid);//Merge and sort on the left, so that the left subsequence is orderly
			mergeSort(arr, mid+1, right);//Merge and sort on the right, so that the right subsequence is orderly
			//merge
			merge(arr, left, right, mid);//Merge two ordered subarrays
		}
	}

	public void merge(int[] arr, int left,int right, int mid) {
		/*
		 * Merge two ordered arrays
		 */
		int[] temp = new int[right-left+1]; //Build a temporary array
		int i=left; //Left subsequence index (understood as pointer)
		int j = mid+1;//Right subsequence index (understood as pointer)
		int k =0;//Index of temporary array (understood as pointer)
		while(i<=mid && j<=right) {
			if(arr[i]<=arr[j]) {
				temp[k++]=arr[i++];
			}
			else {
				temp[k++]=arr[j++];
			}
		}
		while(i<=mid)temp[k++]=arr[i++];//Fill the remaining elements of the left subsequence into temp
		while(j<=right)temp[k++]=arr[j++];//Fill the remaining elements of the right subsequence into temp
		//Copy all the elements in temp back to the original array
		for (int k2 = 0; k2 < temp.length; k2++) {
			arr[k2+left]=temp[k2];
		}
	}
}

4.2 efficiency analysis

• The time complexity of two-way merging sorting is equal to the product of the number of merging trips and the time complexity of each trip. For a table with n elements, the n elements are regarded as leaf nodes. If the child tables generated by merging are regarded as their parent nodes, the merging process corresponds to the process of generating a binary tree from leaf to root. Therefore, the number of merging trips is equal to the height of the binary number minus 1, that is l o g 2 n log_2n log2​n. Each merging needs to move n elements, that is, the time complexity of each merging is O ( n ) O(n) O(n). Therefore, the time complexity of two-way merge sorting is O ( n l o g 2 n ) O(nlog_2n) O(nlog2​n).
• When using two-way merge sorting, the same auxiliary array as the array to be sorted needs to be used as the temporary unit, so the spatial complexity of the sorting method is O ( n ) O(n) O(n), which takes up more space than other sorting methods introduced earlier.
• In two-way merge sort, when every two ordered tables are merged into one ordered table, if the same sort code appears in the two ordered tables, the same sort code in the previous ordered table will be copied first and the same sort code in the next ordered table will be copied later, so as to keep their relative order unchanged. Therefore, two-way merge sort is a stable sort method.

5. Cardinality sorting