Hello everyone, I'm hehaige and focus on the back end. If I can, I want to be a code designer instead of an ordinary coder to witness the growth of hehaige. Your comments and praise are my biggest driving force. If you have any mistakes, please don't hesitate to comment. Thank you very much. Let's support the original! If there is a clerical error in pure hand typing, please forgive me.
1-1: Title Description
Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.
If the tree has more than one mode, return them in any order.
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than or equal to the node's key.
The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
Both the left and right subtrees must also be binary search trees.
Example 1:

Input: root = [1,null,2,2] Output: [2]
Example 2:
Input: root = [0] Output: [0]
Constraints:
The number of nodes in the tree is in the range [1, 104]. -105 <= Node.val <= 105
Follow up: Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
Pass times 74211 submit times 143326
Source: LeetCode
Link: https://leetcode-cn.com/problems/find-mode-in-binary-search-tree
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
1-2: naive solution
☘️ The simplest idea is to traverse all nodes, use hashmap to store the number of occurrences of all numbers, and finally find the one with the largest number of occurrences from hashmap, which is relatively easy, so it is ignored here. It uses extra space, so go straight to the more difficult constant level solution.
1-3: O(N) space complexity
☘️ as we all know, the middle order traversal of the binary search tree must be an incremental sequence, so the most frequent and frequent ones must exist continuously in this incremental sequence, such as 1, 1, 2, 2, 2. Our task is to collect the most common values. Then the main problems encountered in the whole process are:
- There may be more than one value at most, such as 1, 1, 2, 2. Because of this feature, the difficulty goes up directly, so that I thought of this idea and didn't write it out...
☘️ Algorithm flow:
☘️ A base represents the starting point of duplicate values, count represents the number of occurrences of duplicate values, and maxCount represents the one with the most occurrences. There are two situations when comparing values:
- The value and base are equal
- Naturally, count + +, if count > maxCount value, replace maxCount.
- Value and base are not equal
- Reset count=1, and the base is also reset to the new value.
☘️ When I wrote this, I thought it was over at first, but there is a new problem, that is, what if all of them only appear once? Do you have to make such a judgment after the value?
if (count == maxCount) {
result.add(base);
}
The total code becomes like this:
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
maxCount = Math.max(count, maxCount);
} else {
count = 1;
base = root.val;
if (count == maxCount) {
result.add(base);
}
}
traverse(root.right);
}
☘️ Yes, there must be. You think it's over again, not yet! Add I am 1, 2, 2. The new value 2 appears twice. It has to replace the original 1 twice, right? Then you have to clear the result set first and then add a new value. So it became like this:
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
} else {
count = 1;
base = root.val;
if (count == maxCount) {
result.add(base);
}
}
traverse(root.right);
}
☘️ Let's initialize again. The default value of base is infinite, count=maxcount=0, that is, it does not exist. In this way, when the first value is met, the first value will become base, which is easier to understand.
List<Integer> result = new ArrayList<>();
int base = Integer.MIN_VALUE;
int count = 0;
int maxCount = 0;
public int[] findMode(TreeNode root) {
if (root == null) {
return null;
}
traverse(root);
int[] mode = new int[result.size()];
for (int i = 0; i < result.size(); i++) {
mode[i] = result.get(i);
}
return mode;
}
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
} else {
count = 1;
base = root.val;
if (count == maxCount) {
result.add(base);
}
}
traverse(root.right);
}
Tie it first~
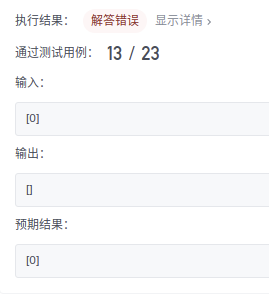
☘️ If you can't see what's wrong with the code, debug it.

☘️ When debug ging, you will find that when there is only one node, maxcount will be updated at the beginning of the algorithm. So you have to add a result at this time.
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
} else {
count = 1;
base = root.val;
if (count == maxCount) {
result.add(base);
}
if (count > maxCount) {
maxCount = count;
// result.clear();
result.add(base);
}
}
traverse(root.right);
}
☘️ Note that you must judge here after count==maxcount. Then I will continue to submit. There's a problem again. Yes, it's normal. Hahaha, let's see what's wrong this time?

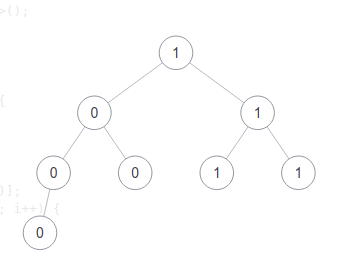
Similarly, I debug until I find a problem.
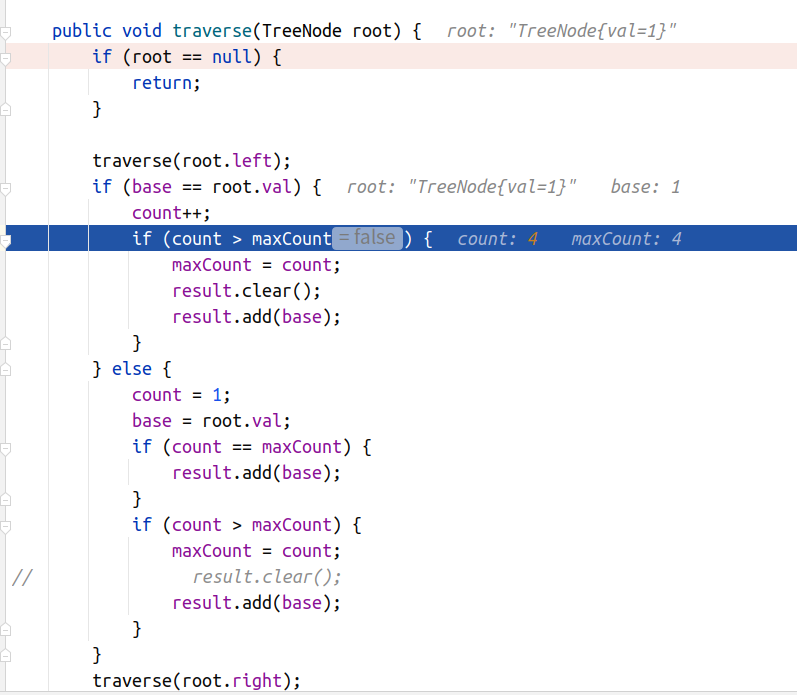
☘️ Yes, when the program reaches the last 1, it is found that count and maxcount are equal, that is, after four zeros, four ones appear. So, you have to add another one.
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
// Newly added part----------
if (count == maxCount) {
result.add(base);
}
//-------------------
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
} else {
count = 1;
base = root.val;
if (count == maxCount) {
result.add(base);
}
if (count > maxCount) {
maxCount = count;
// result.clear();
result.add(base);
}
}
traverse(root.right);
}
Final AC
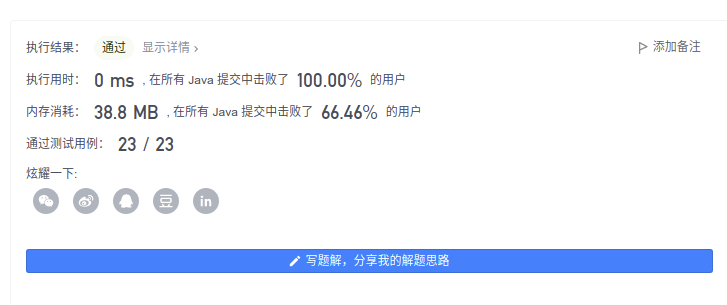
☘️ In order to make the code look more elegant, let's modify it to achieve the final code of the answer:
List<Integer> result = new ArrayList<>();
int base = Integer.MIN_VALUE;
int count = 0;
int maxCount = 0;
public int[] findMode(TreeNode root) {
if (root == null) {
return null;
}
traverse(root);
int[] mode = new int[result.size()];
for (int i = 0; i < result.size(); i++) {
mode[i] = result.get(i);
}
return mode;
}
public void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.left);
if (base == root.val) {
count++;
} else {
count = 1;
base = root.val;
}
if (count == maxCount) {
result.add(base);
}
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
traverse(root.right);
}
Time complexity O(N)
Spatial complexity O(H),H It's the height of the tree
☘️ So see this over? Not yet. I was very confused at the beginning. The answer said that there should be no additional space except for the additional space of the recursive stack, right. But isn't there a list here? I think it should be like this. The answer is to use array storage. This array storage itself has a problem, because the space of the array must be opened up in advance. We don't know the nodes of the tree and how many modes there are, so we can only use list. Changing the return value to list is perfect, and it already meets the meaning of the question.
Spatial complexity of 1-4: O(1) constant level
☘️ To understand this, we must first understand the Morris algorithm. The core of Morris algorithm is to use clues to find the successor position of this node in the binary tree. What is the successor? For example, 1 2 3, the result of middle order traversal is 2 1 3, 1 is the successor of 2, and 2 is the precursor of 1.
☘️ Firstly, the steps of Morris algorithm are given:
- First, cur represents the traversal pointer, if cur Left is empty, that is, when it comes to the leftmost node, cur = cur Right (use the subsequent pointer to return to the root position)
- If cur left != Null. If you have a left child, you should try to find the precursor node of cur. You have to look down to the right along the left child. Find the precursor node and record it as pre.
- If pre Right = = null, that is, the successor is not built, then pre Right = cur, build the subsequent pointer, point to cur, and then cur = cur left
- If pre Right = = cur, that is, there is already a successor node (that is, it has passed through the cur node before, there was no visit before, this visit), cur = cur Right, turn to the right to continue the algorithm. It's like accessing the root after accessing the left. After accessing the root, switch to the right to continue accessing.
public void traverse(TreeNode root) {
TreeNode cur = root;
TreeNode pre = null;
while (cur != null) {
if (cur.left == null) {
System.out.println(cur);
cur = cur.right;
// The function of adding continue is to cur at the end Right = = null,
// Run pre = cur left; Null pointer exception
continue;
}
pre = cur.left;
// Start to find the rightmost node, that is, the precursor node of cur,
// Add pre right != Cur is because if the subsequent node has been built, pre Right will go back to cur,
// It's not the node at the bottom right
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
// Process of building successor nodes
if (pre.right == null) {
pre.right = cur;
// cur continues to build the successor node to the left
cur = cur.left;
}
// The node has been built. It indicates that you have accessed pre before. At this time, you can continue to access cur
if (pre.right == cur) {
pre.right = null;
System.out.println(cur);
cur = cur.right;
}
}
}
☘️ If you can't understand it, just simulate it manually. Here is a draft of my manual simulation, which is a little rough..
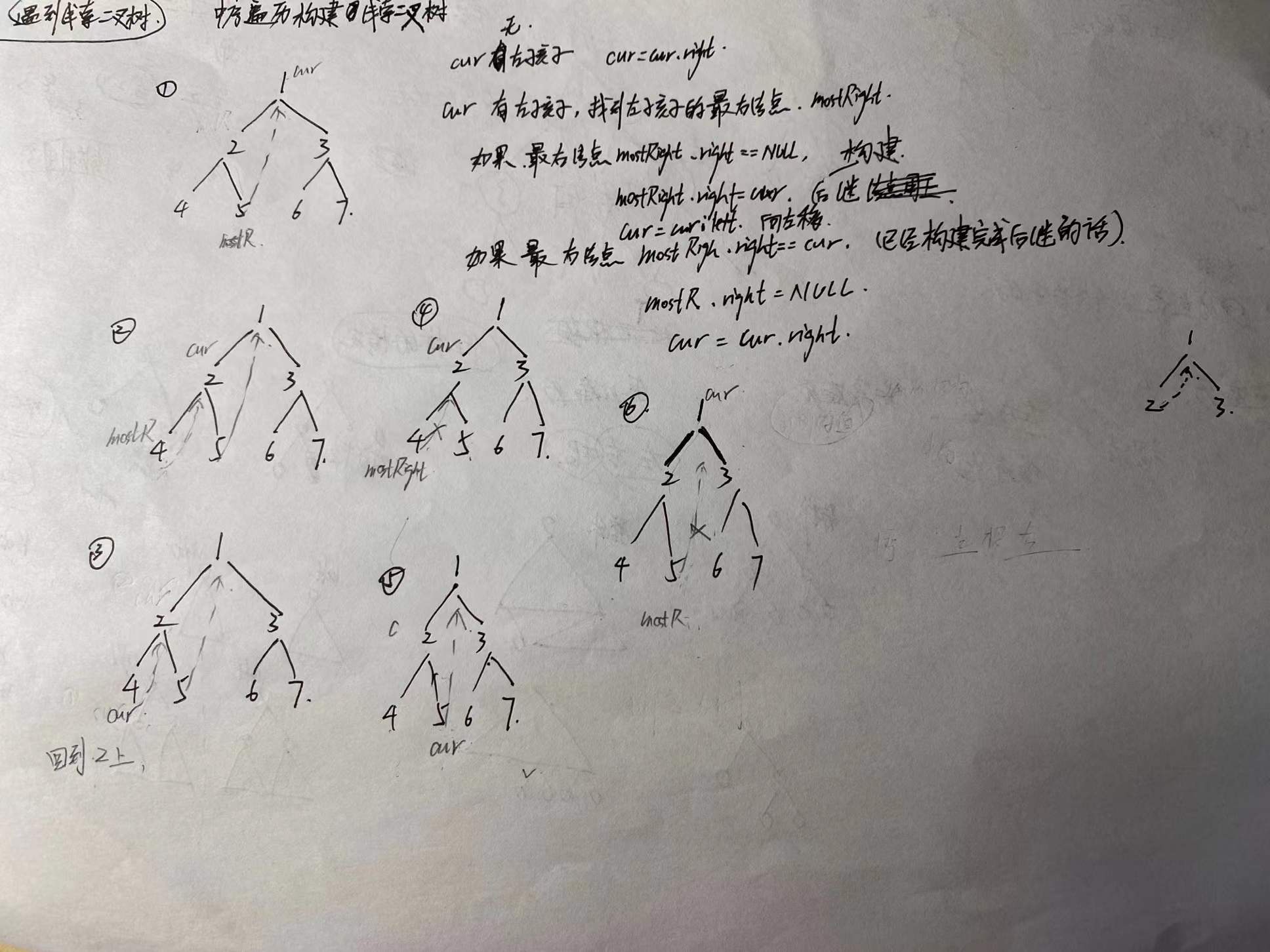
☘️ After this algorithm is written, we can apply it to this problem. You only need to change the operation of accessing the node to the following code:
if (base == root.val) {
count++;
} else {
count = 1;
base = root.val;
}
if (count == maxCount) {
result.add(base);
}
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
The final code is as follows:
class Solution {
List<Integer> result = new ArrayList<>();
int base = Integer.MIN_VALUE;
int count = 0;
int maxCount = 0;
public int[] findMode(TreeNode root) {
if (root == null) {
return null;
}
traverse(root);
int[] mode = new int[result.size()];
for (int i = 0; i < result.size(); i++) {
mode[i] = result.get(i);
}
return mode;
}
private void update(TreeNode root) {
if (base == root.val) {
count++;
} else {
count = 1;
base = root.val;
}
if (count == maxCount) {
result.add(base);
}
if (count > maxCount) {
maxCount = count;
result.clear();
result.add(base);
}
}
public void traverse(TreeNode root) {
TreeNode cur = root;
TreeNode pre = null;
while (cur != null) {
if (cur.left == null) {
// System.out.println(cur);
update(cur);
cur = cur.right;
// The function of adding continue is to cur at the end Right = = null,
// Run pre = cur left; Null pointer exception
continue;
}
pre = cur.left;
// Start to find the rightmost node, that is, the precursor node of cur,
// Add pre right != Cur is because if the subsequent node has been built, pre Right will go back to cur,
// It's not the node at the bottom right
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
// Process of building successor nodes
if (pre.right == null) {
pre.right = cur;
// cur continues to build the successor node to the left
cur = cur.left;
}
// The node has been built. It indicates that you have accessed pre before. At this time, you can continue to access cur
if (pre.right == cur) {
pre.right = null;
// System.out.println(cur);
update(cur);
cur = cur.right;
}
}
}
}
Time complexity O(N),Each node will not be accessed more than twice
Spatial complexity O(1)
☘️ But it really does, spatial complexity O(1).
1-5: summary
☘️ The most important thing today is the Morris algorithm, which can complete the middle order traversal of binary tree without additional space. The core idea is to use precursors and successors, similar to the idea of clue binary tree. Seconds! Seconds! I feel that the complexity of the above O(N) space needs to be written correctly, which is not easy. There are many situations.

Point a praise ~ brother ~, come back next time ~ beauty!