1, Introduction to ant lion algorithm

1. Principle

ALO algorithm simulates the hunting mechanism of ant lion in nature. Their name comes from their unique hunting behavior and their favorite prey. The ant lion moves along a circular path and uses its huge jaw to dig a conical pit in the sand. After digging the trap, hide at the bottom of the cone (as a waiting predator) and wait for the insects (preferably ants) trapped in the pit, as shown in Figure 1. The main steps of random walking of ants, setting traps, trapping ants with traps, capturing prey and reconstructing traps were implemented.

Fig. 1 hunting behavior of ant lion

1. Algorithm steps

11 foraging ants walk randomly

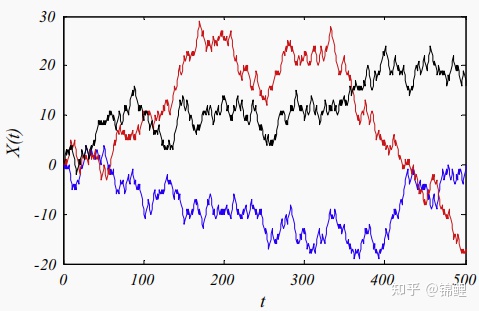
Fig. 2 random walk of ants (3 times)

In order to simulate the hunting ability of ant lion, the method of Roulette is adopted. As shown in Figure 3, suppose that the ant is trapped in only one selected ant lion. In the process of optimization, ant colony algorithm needs to use roulette wheel operator to select ant colony according to the fitness of ant colony. This mechanism provides a higher opportunity for more suitable ant lions to prey on ants.

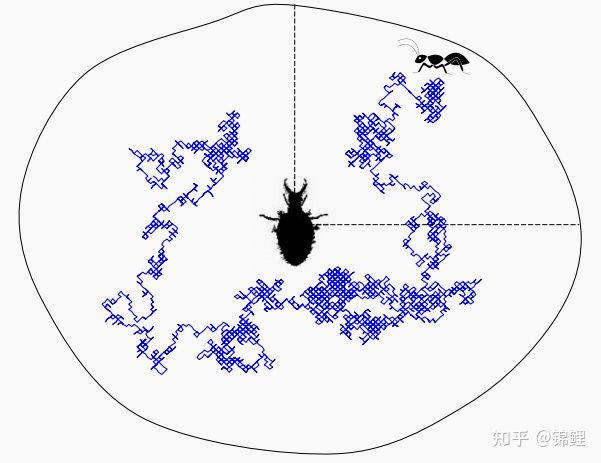
Fig. 3 random walk of ants in ant lion trap

1.2 setting traps

1.3 trap ants

1.4 capture prey and rebuild caves

2. Pseudo code

Figure 4 pseudo code of alo algorithm

2, Adaptive ant lion optimization algorithm for optimization strategy

2.1 adaptive boundary

2.2 optimizing roulette strategy

2.3 dynamic scale factor

Algorithm steps

3, Simulation experiment and result analysis

% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of generations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers

% To run ALO: [Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

function [min_value,Elite_antlion_fitness,Elite_antlion_position,Convergence_curve]=ALO(N,Max_iter,lb,ub,dim,fobj)

% Initialize the positions of antlions and ants
antlion_position=initialization(N,dim,ub,lb);
ant_position=initialization(N,dim,ub,lb);

% Initialize variables to save the position of elite, sorted antlions, 
% convergence curve, antlions fitness, and ants fitness
Sorted_antlions=zeros(N,dim);
Elite_antlion_position=zeros(1,dim);
Elite_antlion_fitness=inf;
Convergence_curve=zeros(1,Max_iter);
antlions_fitness=zeros(1,N);
ants_fitness=zeros(1,N);

% Calculate the fitness of initial antlions and sort them
for i=1:size(antlion_position,1)
    antlions_fitness(1,i)=fobj(antlion_position(i,:)); 
end

[sorted_antlion_fitness,sorted_indexes]=sort(antlions_fitness);
    
for newindex=1:N
     Sorted_antlions(newindex,:)=antlion_position(sorted_indexes(newindex),:);
end
    
Elite_antlion_position=Sorted_antlions(1,:);
Elite_antlion_fitness=sorted_antlion_fitness(1);

% Main loop start from the second iteration since the first iteration 
% was dedicated to calculating the fitness of antlions
Current_iter=2; 
while Current_iter<Max_iter+1
    
    % This for loop simulate random walks
    for i=1:size(ant_position,1)
        % Select ant lions based on their fitness (the better anlion the higher chance of catching ant)
        Rolette_index=RouletteWheelSelection(1./sorted_antlion_fitness);
        if Rolette_index==-1  
            Rolette_index=1;
        end
      
        % RA is the random walk around the selected antlion by rolette wheel
        RA=Random_walk_around_antlion(dim,Max_iter,lb,ub, Sorted_antlions(Rolette_index,:),Current_iter);
        
        % RA is the random walk around the elite (best antlion so far)
        [RE]=Random_walk_around_antlion(dim,Max_iter,lb,ub, Elite_antlion_position(1,:),Current_iter);
        
        ant_position(i,:)= (RA(Current_iter,:)+RE(Current_iter,:))/2; % Equation (2.13) in the paper          
    end
    
    for i=1:size(ant_position,1)  
        
        % Boundar checking (bring back the antlions of ants inside search
        % space if they go beyoud the boundaries
        Flag4ub=ant_position(i,:)>ub;
        Flag4lb=ant_position(i,:)<lb;
        ant_position(i,:)=(ant_position(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;  
        
        ants_fitness(1,i)=fobj(ant_position(i,:));        
       
    end
    
    % Update antlion positions and fitnesses based of the ants (if an ant 
    % becomes fitter than an antlion we assume it was cought by the antlion  
    % and the antlion update goes to its position to build the trap)
    double_population=[Sorted_antlions;ant_position];
    double_fitness=[sorted_antlion_fitness ants_fitness];
        
    [double_fitness_sorted I]=sort(double_fitness);
    double_sorted_population=double_population(I,:);
        
    antlions_fitness=double_fitness_sorted(1:N);
    Sorted_antlions=double_sorted_population(1:N,:);
        
    % Update the position of elite if any antlinons becomes fitter than it
    if antlions_fitness(1)<Elite_antlion_fitness 
        Elite_antlion_position=Sorted_antlions(1,:);
        Elite_antlion_fitness=antlions_fitness(1);
    end
      
    % Keep the elite in the population
    Sorted_antlions(1,:)=Elite_antlion_position;
    antlions_fitness(1)=Elite_antlion_fitness;
  
    % Update the convergence curve
    Convergence_curve(Current_iter)=Elite_antlion_fitness;

    % Display the iteration and best optimum obtained so far
    if mod(Current_iter,1)==0
        display(['At iteration ', num2str(Current_iter), ' the elite fitness is ', num2str(Elite_antlion_fitness)]);
    end
min_value(Current_iter)=Elite_antlion_fitness;
    Current_iter=Current_iter+1; 
end

The improved ant lion algorithm (PSALO) is compared with the original ant lion algorithm (ALO) and the bottle sea squirt swarm algorithm (SSA). The simulation is 30 times, 500 iterations each time, and the population size is 30. Take F1~F3 as an example.
The following figure shows the comparison curve of F1.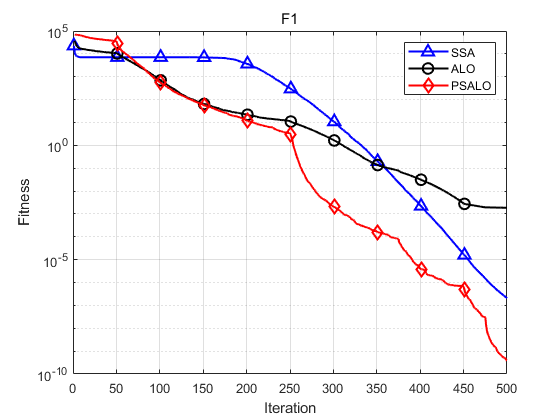
The maximum, minimum, average and standard deviation of the three algorithms are shown as follows:

Function: F1
SSA: Maximum: 1.976e-06,minimum value:3.3803e-08,average value:2.093e-07,standard deviation:3.9333e-07
ALO: Maximum: 0.0097103,minimum value:0.00022597,average value:0.0018599,standard deviation:0.0022659
PSALO: Maximum: 1.1972e-09,minimum value:1.7294e-11,average value:3.9346e-10,standard deviation:3.428e-10

The following figure is the comparison curve of F2.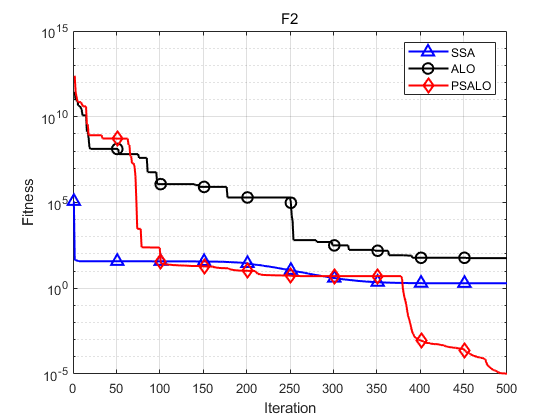

The maximum, minimum, average and standard deviation of the three algorithms are shown as follows:

Function: F2
SSA: Maximum: 5.0543,minimum value:0.12765,average value:1.9419,standard deviation:1.4266
ALO: Maximum: 127.5844,minimum value:5.1073,average value:56.8097,standard deviation:48.045
PSALO: Maximum: 2.1726e-05,minimum value:4.3211e-06,average value:1.0354e-05,standard deviation:5.0614e-06

The following figure shows the comparison curve of F3.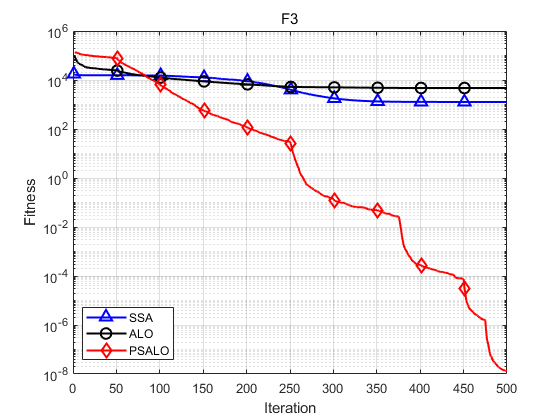
The maximum, minimum, average and standard deviation of the three algorithms are shown as follows:

Function: F3
SSA: Maximum: 3008.01,minimum value:236.0645,average value:1270.2519,standard deviation:616.1047
ALO: Maximum: 13305.4836,minimum value:1777.0977,average value:4707.7349,standard deviation:2533.4001
PSALO: Maximum: 3.2929e-08,minimum value:2.662e-09,average value:1.3591e-08,standard deviation:8.0512e-09

In conclusion, PSALO has good evolutionary optimization performance, and its solution accuracy, convergence speed and stability are excellent.

4, References

[1] Liu jingsen, Huo Yu, Li Yu Adaptive ant lion optimization algorithm for optimization strategy [J]. Pattern recognition and artificial intelligence, 2020,33 (2): 121-132

If you like, you can pay attention to me