C language to realize quick sorting and its system optimization and analysis
catalogue
I Implementation of quick sort
3. Implementation of the function Partition()
II System optimization of quick sort
1. Optimize the selection of keyword pivotkey
2. Optimize unnecessary exchange (turn exchange into assignment)
3. Optimize recursive operation
4.!!!! Optimized complete code!!!!!
I Implementation of quick sort
1. Implementation ideas
The basic idea of quick sorting is: first, find a random number in the array to be sorted (in fact, it is tricky to find this number, which will be discussed later). This number is also called keyword. The array is divided into left and right parts through one sorting. The left part is smaller than the keyword, the middle is the keyword, and the right part is larger than the keyword. Then the left and right parts can continue to sort as just until the whole array is in order.
for example
Unordered array 26,1,7,56,34,23,77,87,22,43,16,66
1. Let's choose a keyword first, for example, 26
2. After the first sorting, the left part is smaller than the keyword, the middle part is the keyword, and the right part is larger than the keyword
I.e. 16 1 7 22 23 26 77 87 34 43 56 66
3. 16 1 7 22 23 is the left part
4. 26 is the keyword, i.e. the middle part
5. 77 87 34 43 56 66 is the right part
6. Then we can continue the operation on the left and right parts, so the core code of quick sorting is how to divide the array into the left and right parts!! Does it sound simple!! Next, let's implement it
2.QSort implementation
void QSort(int* arr, int low,int high)//low is the first subscript of the array, that is, 0; high is the last subscript of the array
{
int pivot;//Subscript of keyword
if (low < high)
{
pivot = Partition(arr, low, high);//Get the keyword subscript to divide the array into left and right parts
QSort(arr, low, pivot - 1);//Continue sorting the left part
QSort(arr, pivot + 1, high);//Continue sorting the right part
}
}
int main()
{
int arr[] = { 26,1,7,56,34,23,77,87,22,43,16,66 };
QSort(arr, 0,(sizeof(arr) / sizeof(arr[0])-1));
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
}Here, we define an array int arr [] = {26,1,7,56,34,23,77,87,22,43,16,66}. What we need to do is to get the subscript of the keyword in "pivot = Partition(arr, low, high)" and turn the array into:
1. Keyword in the middle
2. The left side of the keyword is less than or equal to the value of the keyword
3. The right side of the keyword is greater than or equal to the value of the keyword
This is also the function of the function Partition(), so next we need to find a way to implement the function Partition().
3. Implementation of the function Partition()
void swap(int* arr, int x, int y)
{
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
int Partition(int* arr, int low, int high)
{
int pivotkey = arr[low];//Pivot key is a keyword. Just find one here. For convenience, we take the first element of the array
while (low < high)//When low and high are equal, it means that low and high point to the subscript of the keyword at the same time
{
while (low < high && arr[high] >= pivotkey)//Start from the right to the left of the array to find if there is anything smaller than the keyword. If there is, jump out of the loop and exchange with the number on the left of the keyword to ensure that the small numbers are on the left of the keyword.
{
high--;
}
swap(arr, low, high);//Function of exchanging values
while (low < high && arr[low] <= pivotkey)Start from the left to the right of the array to find out if there is any larger than the keyword. If there is, jump out of the loop and exchange with the number on the right of the keyword to ensure that the large numbers are on the right of the keyword.
{
low++;
}
swap(arr, low, high);
}
return low;//Return keyword subscripts, low and high
}After Partition() in turn, the array arr [] becomes two parts centered on the first element 26 of the array arr= 16 1 7 22 23 ^ 26 77 87 34 43 56 66. The right part of 26 is larger than 26 and the left part of 26 is smaller than 26. Then continue to recursively sort the left and right sides again, that is, the two sentences of code with a red line in the following figure
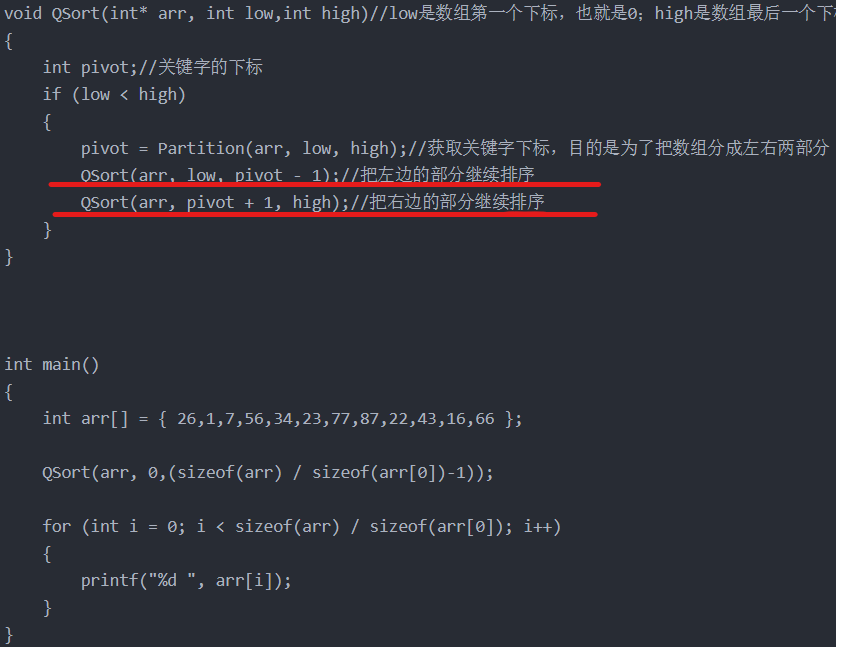
4. Complete code
void swap(int* arr, int x, int y)
{
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
int Partition(int* arr, int low, int high)
{
int pivotkey = arr[low];//Pivot key is a keyword. Just find one here. For convenience, we take the first element of the array
while (low < high)//When low and high are equal, it means that low and high point to the subscript of the keyword at the same time
{
while (low < high && arr[high] >= pivotkey)//Start from the right to the left of the array to find if there is anything smaller than the keyword. If there is, jump out of the loop and exchange with the number on the left of the keyword to ensure that the small numbers are on the left of the keyword.
{
high--;
}
swap(arr, low, high);//Function of exchanging values
while (low < high && arr[low] <= pivotkey)Start from the left to the right of the array to find out if there is any larger than the keyword. If there is, jump out of the loop and exchange with the number on the right of the keyword to ensure that the large numbers are on the right of the keyword.
{
low++;
}
swap(arr, low, high);
}
return low;//Return keyword subscripts, low and high
}
void QSort(int* arr, int low,int high)//low is the first subscript of the array, that is, 0; high is the last subscript of the array
{
int pivot;//Subscript of keyword
if (low < high)
{
pivot = Partition(arr, low, high);//Get the keyword subscript to divide the array into left and right parts
QSort(arr, low, pivot - 1);//Continue sorting the left part
QSort(arr, pivot + 1, high);//Continue sorting the right part
}
}
int main()
{
int arr[] = { 26,1,7,56,34,23,77,87,22,43,16,66 };
QSort(arr, 0,(sizeof(arr) / sizeof(arr[0])-1));
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
}Operation effect:
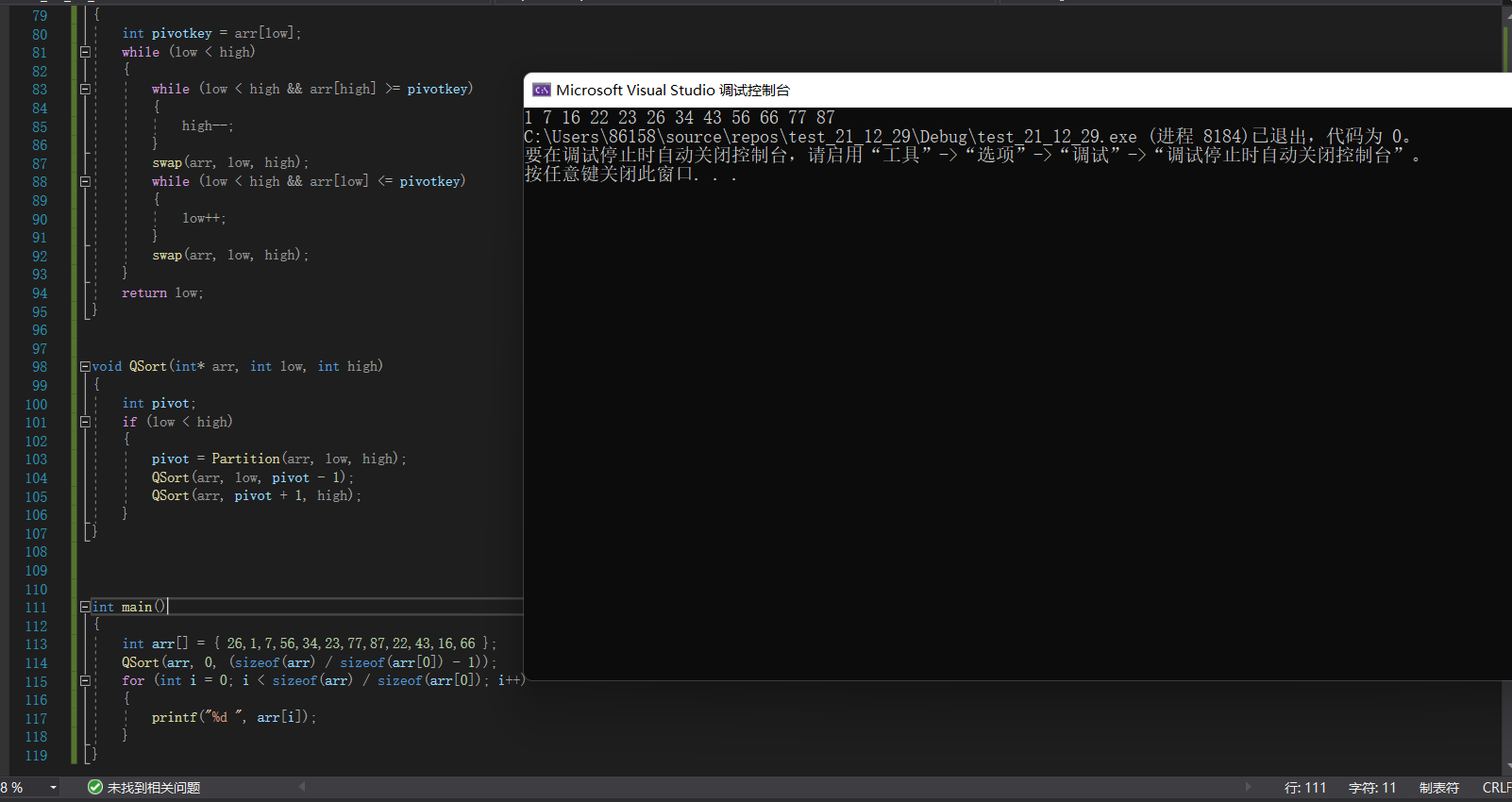
II System optimization of quick sort
1. Optimize the selection of keyword pivotkey
For convenience, we always select the first element of the array as the keyword. There are certain disadvantages if we are so arbitrary. For example, the array to be sorted just now becomes arr [] = {1,26,7,56,34,23,77,87,22,43,16,66}. If we select the first element 1, it is obviously unreasonable to select 1 compared with any other number, So the keywords we just chose have a great impact on our sorting speed.
Therefore, we came up with a way to take a number from the left, middle and right of the array, and then take the one in the middle of the three numbers as the keyword pivot key. This is indeed a good method in small-scale sorting, but its role is also minimal in large-scale arrays. Therefore, in large-scale sorting, sometimes 27 numbers take 9 and then take 3 and then take 1, and 9 take 3 and then take 1. The reason is the same, that is, to find a suitable keyword and speed up sorting.
Therefore, we add these lines of code before determining the keyword pivotkey
int mid = low + (high - low) / 2;//Determines the subscript of the intermediate element
if (arr[low] > arr[high])
{
swap(arr, low, high);//Exchange data at the left and right ends to keep the left end small
}
if (arr[mid] > arr[high])
{
swap(arr, high, mid);//Exchange data at the middle right end to ensure that the middle is small
}
if (arr[mid] > arr[low])
{
swap(arr, mid, low);//Exchange the data of the left and middle ends to ensure that the left end is larger than the middle one, so that the middle of the three numbers will run to the far left
}The function partition () becomes like this
int Partition(int* arr, int low, int high)
{
int mid = low + (high - low) / 2;//Determines the subscript of the intermediate element
if (arr[low] > arr[high])
{
swap(arr, low, high);//Exchange data at the left and right ends to keep the left end small
}
if (arr[mid] > arr[high])
{
swap(arr, high, mid);//Exchange data at the middle right end to ensure that the middle is small
}
if (arr[mid] > arr[low])
{
swap(arr, mid, low);//Exchange the data of the left and middle ends to ensure that the left end is larger than the middle one, so that the middle of the three numbers will run to the far left
}
int pivotkey = arr[low];//Pivot key is a keyword. Just find one here. For convenience, we take the first element of the array
while (low < high)//When low and high are equal, it means that low and high point to the subscript of the keyword at the same time
{
while (low < high && arr[high] >= pivotkey)//Start from the right to the left of the array to find if there is anything smaller than the keyword. If there is, jump out of the loop and exchange with the number on the left of the keyword to ensure that the small numbers are on the left of the keyword.
{
high--;
}
swap(arr, low, high);//Function of exchanging values
while (low < high && arr[low] <= pivotkey)Start from the left to the right of the array to find out if there is any larger than the keyword. If there is, jump out of the loop and exchange with the number on the right of the keyword to ensure that the large numbers are on the right of the keyword.
{
low++;
}
swap(arr, low, high);
}
return low;//Return keyword subscripts, low and high
}2. Optimize unnecessary exchange (turn exchange into assignment)
We only need to back up a copy of the keywords before dividing the array into the left and right parts, and then in the sorting process, the exchange between numbers is directly changed to assignment, which will reduce a lot of exchange steps
int pivotkey = arr[low];
int tem = pivotkey;//Backup keyword
while (low < high)
{
while (low < high && arr[high] >= pivotkey)
{
high--;
}
arr[low] = arr[high];//Assignment rather than exchange
while (low < high && arr[low] <= pivotkey)
{
low++;
}
arr[high] = arr[low];//Assignment rather than exchange
}
arr[low] = tem;//Return the value of the keyword to its locationThe principle is the same. Find a small number on the right, assign it to the left, find a large number on the left, and assign it to the right. Anyway, in the end, low and high will point to the subscript of the keyword at the same time, and then return the value of the keyword to it.
After the above operations, our Partition() function becomes like this
int Partition(int* arr, int low, int high)
{
int mid = low + (high - low) / 2;//Determines the subscript of the intermediate element
if (arr[low] > arr[high])
{
swap(arr, low, high);//Exchange data at the left and right ends to keep the left end small
}
if (arr[mid] > arr[high])
{
swap(arr, high, mid);//Exchange data at the middle right end to ensure that the middle is small
}
if (arr[mid] > arr[low])
{
swap(arr, mid, low);//Exchange the data of the left and middle ends to ensure that the left end is larger than the middle one, so that the middle of the three numbers will run to the far left
}
int pivotkey = arr[low];//Pivot key is a keyword. Just find one here. For convenience, we take the first element of the array
int tem = pivotkey;//Backup keyword
while (low < high)//When low and high are equal, it means that low and high point to the subscript of the keyword at the same time
{
while (low < high && arr[high] >= pivotkey)//Start from the right to the left of the array to find if there is anything smaller than the keyword. If there is, jump out of the loop and exchange with the number on the left of the keyword to ensure that the small numbers are on the left of the keyword.
{
high--;
}
arr[low] = arr[high];//Assignment rather than exchange
while (low < high && arr[low] <= pivotkey)Start from the left to the right of the array to find out if there is any larger than the keyword. If there is, jump out of the loop and exchange with the number on the right of the keyword to ensure that the large numbers are on the right of the keyword.
{
low++;
}
arr[high] = arr[low];//Assignment rather than exchange
}
arr[low] = tem;//Return the value of the keyword to its location
return low;//Return keyword subscripts, low and high
}3. Optimize recursive operation
Let's change the function of QSort() to
void QSort(int* arr, int low,int high)
{
int pivot;
while (low < high)//if becomes while
{
pivot = Partition(arr, low, high);
QSort(arr, low, pivot - 1);
low = pivot + 1;//When low is used up, it will not be used anyway, and it will become the original qsort (arr, pivot+1, high); pivot+1, continue to sort recursively
}
}In this way, we reduce the number of recursion and greatly improve the speed!!
4.!!!! Optimized complete code!!!!!
void swap(int* arr, int x, int y)
{
int tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
int Partition(int* arr, int low, int high)
{
int mid = low + (high - low) / 2;//Determines the subscript of the intermediate element
if (arr[low] > arr[high])
{
swap(arr, low, high);//Exchange data at the left and right ends to keep the left end small
}
if (arr[mid] > arr[high])
{
swap(arr, high, mid);//Exchange data at the middle right end to ensure that the middle is small
}
if (arr[mid] > arr[low])
{
swap(arr, mid, low);//Exchange the data of the left and middle ends to ensure that the left end is larger than the middle one, so that the middle of the three numbers will run to the far left
}
int pivotkey = arr[low];//Pivot key is a keyword. Just find one here. For convenience, we take the first element of the array
int tem = pivotkey;//Backup keyword
while (low < high)//When low and high are equal, it means that low and high point to the subscript of the keyword at the same time
{
while (low < high && arr[high] >= pivotkey)//Start from the right to the left of the array to find if there is anything smaller than the keyword. If there is, jump out of the loop and exchange with the number on the left of the keyword to ensure that the small numbers are on the left of the keyword.
{
high--;
}
arr[low] = arr[high];//Assignment rather than exchange
while (low < high && arr[low] <= pivotkey)Start from the left to the right of the array to find out if there is any larger than the keyword. If there is, jump out of the loop and exchange with the number on the right of the keyword to ensure that the large numbers are on the right of the keyword.
{
low++;
}
arr[high] = arr[low];//Assignment rather than exchange
}
arr[low] = tem;//Return the value of the keyword to its location
return low;//Return keyword subscripts, low and high
}
void QSort(int* arr, int low,int high)
{
int pivot;
while (low < high)//if becomes while
{
pivot = Partition(arr, low, high);
QSort(arr, low, pivot - 1);
low = pivot + 1;//When low is used up, it will not be used anyway, and it will become the original qsort (arr, pivot+1, high); pivot+1, continue to sort recursively
}
}
int main()
{
int arr[] = { 26,1,7,56,34,23,77,87,22,43,16,66 };
QSort(arr, 0,(sizeof(arr) / sizeof(arr[0])-1));
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
}Operation effect
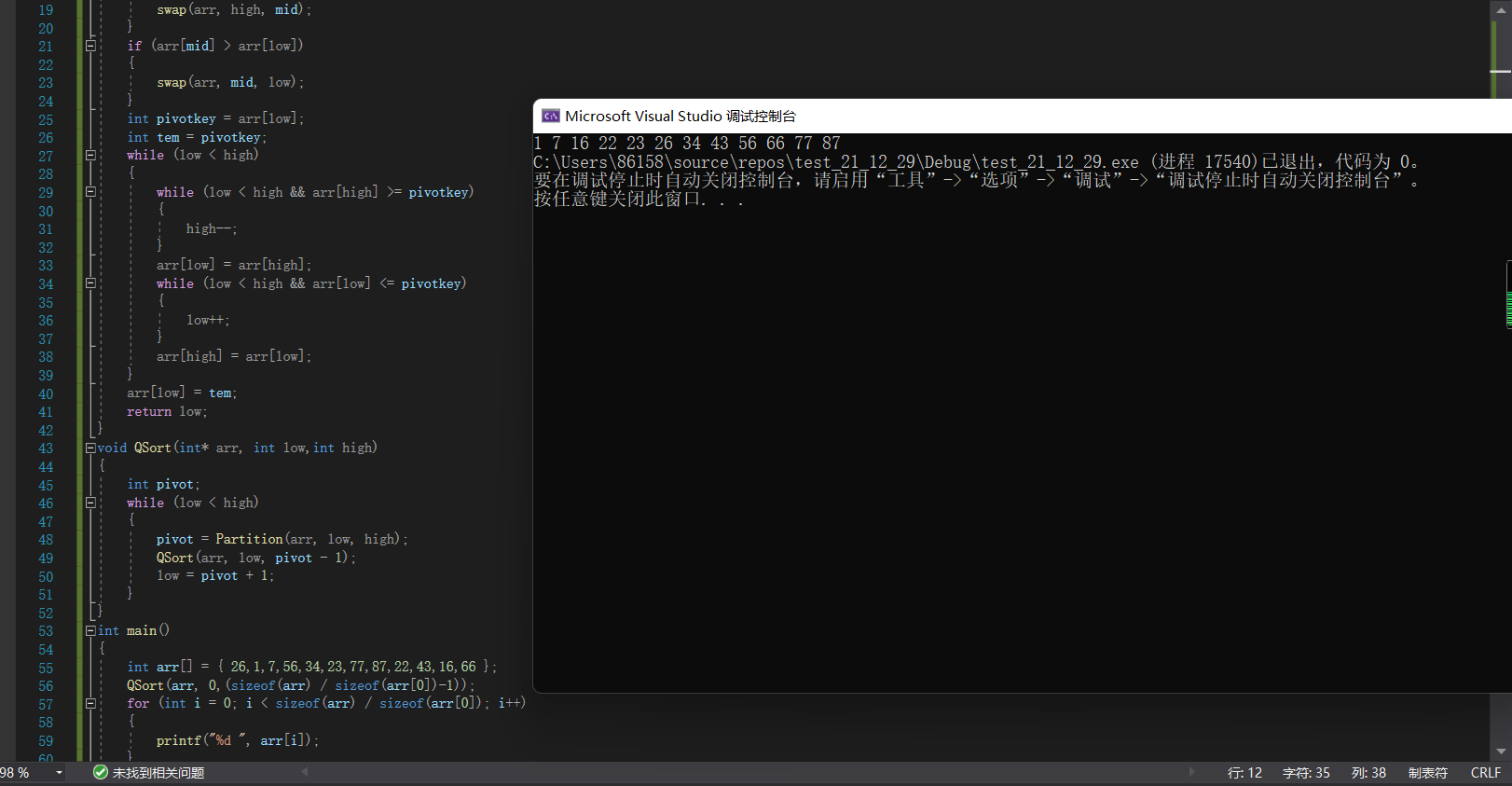
III epilogue
In fact, many library functions of computer language have quick sort function. Although they are different, the effect and speed are the same. If you are interested in the quick sort library function qsort of C language, you can read another explanation about qsort by the blogger, which is very detailed. Finally, you are welcome to leave a message if you don't understand it~
✨ Those who like and feel useful might as well give praise and attention~ ❤️
✨ Your attention is the biggest motivation for bloggers to create ~!!! Thanks for reading!!!!