1, Title Requirements

• Give you an integer n, please generate and return all different binary search trees composed of N nodes with different node values from 1 to N, and you can return the answers in any order.
• Example 1:

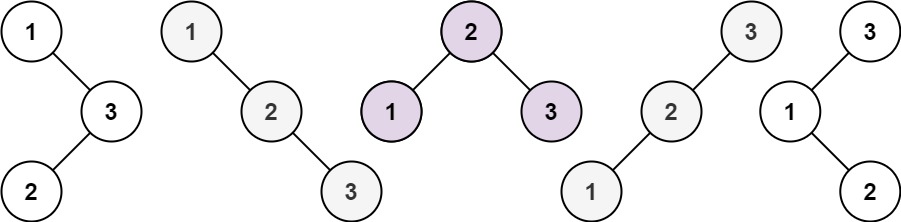
Input: n = 3
 Output:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

• Example 2:

Input: n = 1
 Output:[[1]]

2, Solving algorithm

① Recursion

• We can use the properties of binary tree to find: all values of the left subtree are less than the root node, and all values of the right subtree are greater than the root node, so if we find all the possibilities of 1... n.
• We only need to take 1 as the root node, [] null as the left subtree, and all the possibilities of [2... n] as the right subtree;
• 2 as the root node, [1] as the left subtree, and all possible of [3... n] as the right subtree;
• 3 as the root node, all possibilities of [1, 2] as the left subtree, all possibilities of [4... n] as the right subtree, and then the left subtree and the right subtree are combined in two;
• 4 as the root node, all the possibilities of [1, 2, 3] as the left subtree, all the possibilities of [5... n] as the right subtree, and then the left subtree and the right subtree are combined
• n as the root node, all possible of [1... n] as the left subtree and [] as the right subtree.
• As for all possibilities of [2... n] and [4... n] and other situations, we can use the above method to take each number as the root node, and then combine all possible left and right subtrees.
• If there is only one number, then all may be one case. Take the number as a tree. If it is [], it returns null.
• Java example:

public List<TreeNode> generateTrees(int n) {
    List<TreeNode> ans = new ArrayList<TreeNode>();
    if (n == 0) {
        return ans;
    }
    return getAns(1, n);

}

private List<TreeNode> getAns(int start, int end) { 
    List<TreeNode> ans = new ArrayList<TreeNode>();
    // There are no numbers at this time. Add null to the result
    if (start > end) {
        ans.add(null);
        return ans;
    }
    // There is only one number. The current number is added to the result as a tree
    if (start == end) {
        TreeNode tree = new TreeNode(start);
        ans.add(tree);
        return ans;
    }
    // Try each number as the root node
    for (int i = start; i <= end; i++) {
        // Get all possible left subtrees
        List<TreeNode> leftTrees = getAns(start, i - 1);
         // Get all possible right subtrees
        List<TreeNode> rightTrees = getAns(i + 1, end);
        // Left subtree right subtree pairwise combination
        for (TreeNode leftTree : leftTrees) {
            for (TreeNode rightTree : rightTrees) {
                TreeNode root = new TreeNode(i);
                root.left = leftTree;
                root.right = rightTree;
                // Add to the final result
                ans.add(root);
            }
        }
    }
    return ans;
}

② Dynamic programming 1

• Most recursion can be rewritten with the idea of dynamic programming. For example, n = 3:

All solutions where the number of numbers is 0
null
 All solutions where the number of numbers is 1
1
2
3
 The number of numbers is all solutions of 2. We only need to consider continuous numbers
[ 1 2 ]
  1  
   \    
    2
   2
  /
 1
    
[ 2 3 ]
  2  
   \    
    3
   3
  /
 2
 If you find all three numbers.
[ 1 2 3 ]
Using solution①The idea of recursion is to take each number as the root node, and then consider the possibility of left subtree and right subtree
1 As the root node, the left subtree is [] Of all the possibilities, the right subtree is [ 2 3 ] All the possibilities are combined by using the results obtained before.
    1
  /   \
null   2
        \
         3

    1
  /   \
null   3
      /
     2 
    
2 As the root node, the left subtree is [ 1 ] Of all the possibilities, the right subtree is  [ 3 ] All the possibilities are combined by using the results obtained before.
    2
  /   \
 1     3

3 As the root node, the left subtree is [ 1 2 ] Of all the possibilities, the right subtree is [] All the possibilities are combined by using the results obtained before.
     3
   /   \
  1   null
   \
    2

      3
    /   \
   2   null 
  /
 1

• Then, using the above idea, you can basically write code, that is, find all possibilities with length 1 and all possibilities with length 2... Up to n. But note that when finding all the possibilities with length 2, we need to ask for all the possibilities of [1,2] and all the possibilities of [2,3], which is only the case of n = 3. If n equals 100, we need to find more [1,2], [2,3], [3,4]... [99, 100], so can we optimize it?
• Careful observation shows that there are only two possible structures with a length of 2:

  x  
 /    
y

y
 \
  x

• Look at [1,2] and [2,3] deduced before, but the numbers are different and the structure is exactly the same:

[ 1 2 ]
  1  
   \    
    2
   2
  /
 1
    
[ 2 3 ]
  2  
   \    
    3
   3
  /
 2

• Therefore, when n = 100, when finding all cases with length 2, it is not necessary to find all cases of [1,2], [2,3], [3,4]... [99,100], just find all cases of [1,2].
• To generalize to any length len, in fact, only all the cases of [1, 2... Len] are required. The next question follows. What about those [2,3], [3,4]... [99,100] that don't ask?
• For example: n = 100. At this time, we find that 98 is the root node. According to the previous derivation, we need all cases of [1, 2... 97] with length 97 as the left subtree and all cases of [99, 100] with length 2 as the right subtree.
• All the cases of [1, 2... 97] happen to be [1, 2... len], which has been solved. But what about [99 100]? We only ask for all cases of [1,2], and the answer is obvious. In all cases of [1,2], add a deviation 98 to each number, that is, add the value of the root node.

[ 1 2 ]
  1  
   \    
    2
   2
  /
 1
    
[ 99 100 ]
  1 + 98
   \    
    2 + 98
   2 + 98
  /
 1 + 98

Namely
  99  
   \    
    100
   100
  /
 99

• Therefore, a function is required to copy the tree and add deviation:

private TreeNode clone(TreeNode n, int offset) {
    if (n == null) {
        return null;
    }
    TreeNode node = new TreeNode(n.val + offset);
    node.left = clone(n.left, offset);
    node.right = clone(n.right, offset);
    return node;
}

• Through all the above analysis, the code can be written. The overall idea is to find all cases with length 2 and all cases with length 3 until n. For all cases with a length of len, you only need to find all cases representing [1, 2... Len]. For others, add a deviation and the current root node:

public List<TreeNode> generateTrees(int n) {
    ArrayList<TreeNode>[] dp = new ArrayList[n + 1];
    dp[0] = new ArrayList<TreeNode>();
    if (n == 0) {
        return dp[0];
    }
    dp[0].add(null);
    // Length 1 to n
    for (int len = 1; len <= n; len++) {
        dp[len] = new ArrayList<TreeNode>();
        // Taking different numbers as the root node, you only need to consider len
        for (int root = 1; root <= len; root++) {
            int left = root - 1;     // Length of left subtree
            int right = len - root;  // Length of right subtree
            for (TreeNode leftTree : dp[left]) {
                for (TreeNode rightTree : dp[right]) {
                    TreeNode treeRoot = new TreeNode(root);
                    treeRoot.left = leftTree;
                    // Clone the right subtree and add deviation
                    treeRoot.right = clone(rightTree, root);
                    dp[len].add(treeRoot);
                }
            }
        }
    }
    return dp[n];
}

private TreeNode clone(TreeNode n, int offset) {
    if (n == null) {
        return null;
    }
    TreeNode node = new TreeNode(n.val + offset);
    node.left = clone(n.left, offset);
    node.right = clone(n.right, offset);
    return node;
}

• It is worth noting that we do not have clone s for all the left subtrees, that is, many subtrees are shared and will look like the following in memory:

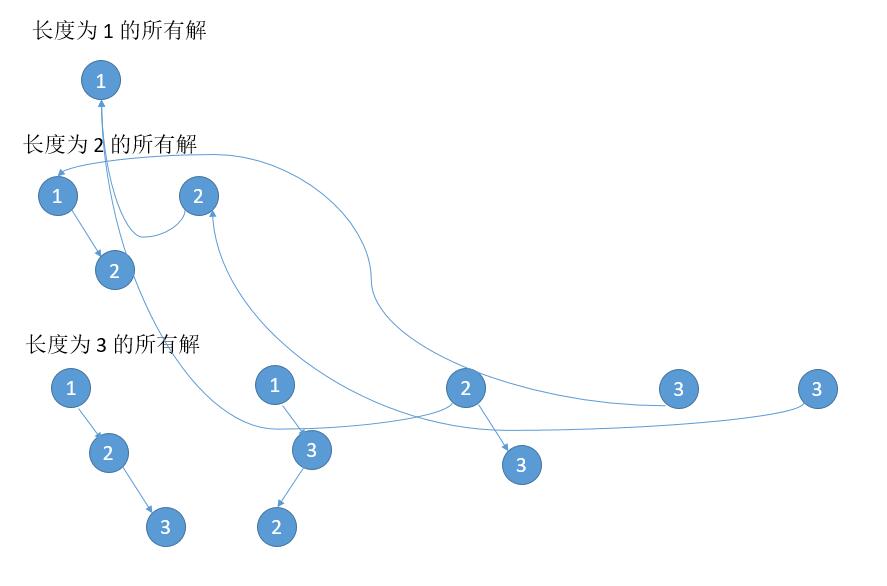
• That is, the left subtree uses the previous subtree without opening up a new space.

③ Dynamic programming 2

• Dynamic programming 1 of solution ② completely imitates the idea of recursion of solution 2, and then shares an idea of dynamic programming:

consider [] All solutions of
null

consider [ 1 ] All solutions of
1

consider [ 1 2 ] All solutions of
  2
 /
1

 1
  \
   2

consider [ 1 2 3 ] All solutions of
    3
   /
  2
 /
1

   2
  / \
 1   3
    
     3
    /
   1
    \
     2
       
   1
     \
      3
     /
    2
    
  1
    \
     2
      \
       3

• A rule can be found by careful analysis. First of all, the number we add each time is greater than all the previous numbers, so the location of the newly added number can only be the root node or the right child of the root node, the right child of the right child, the right child of the right child, and so on. In short, it must be the right. Secondly, the original subtree where the new number is located can be changed to the left child of the current inserted number, because the inserted number is the largest.

For the lower solution 
  2
 /
1

Then add 3
1.Put 3 on the root node
    3
   /
  2
 /
1

2. Put 3 on the right child of the root node
   2
  / \
 1   3
 
For the lower solution
 1
  \
   2

Then add 3
1.Put 3 on the root node
     3
    /
   1
    \
     2
       
2. Put 3 on the right child of the root node, and the original subtree is the left child of 3       
      1
        \
         3
        /
      2

3. Put 3 on the right child of the root node
  1
    \
     2
      \
       3

• The above is all the processes of pushing out [1 2 3] according to [1 2]. You can write the sample code. Because all the current solutions only need the last solution, all need only two list s, pre saves all the previous solutions, and cur calculates all the current solutions:

public List<TreeNode> generateTrees(int n) {
    List<TreeNode> pre = new ArrayList<TreeNode>();
    if (n == 0) {
        return pre;
    }
    pre.add(null);
    // Add one number at a time
    for (int i = 1; i <= n; i++) {
        List<TreeNode> cur = new ArrayList<TreeNode>();
        // Traverse all previous solutions
        for (TreeNode root : pre) {
            // Insert into root node
            TreeNode insert = new TreeNode(i);
            insert.left = root;
            cur.add(insert);
            // Insert into right child, right child's right child Find children n times at most
            for (int j = 0; j <= n; j++) {
                TreeNode root_copy = treeCopy(root); // Copy the current tree
                TreeNode right = root_copy; 		 // Find the location where you want to insert the right child
                int k = 0;
                // Traverse j times to find the right child
                for (; k < j; k++) {
                    if (right == null)
                        break;
                    right = right.right;
                }
                // Arrival null early end
                if (right == null)
                    break;
                // Save the subtree of the current right child's position as the left child of the inserted node
                TreeNode rightTree = right.right;
                insert = new TreeNode(i);
                right.right = insert;    // The right child is the inserted node
                insert.left = rightTree; //The left child of the inserted node is updated to the subtree before the insertion position
                //Add to results
                cur.add(root_copy);
            }
        }
        pre = cur;

    }
    return pre;
}


private TreeNode treeCopy(TreeNode root) {
    if (root == null) {
        return root;
    }
    TreeNode newRoot = new TreeNode(root.val);
    newRoot.left = treeCopy(root.left);
    newRoot.right = treeCopy(root.right);
    return newRoot;
}

④ Backtracking method (LeetCode official solution)

• The key property of binary search tree is that the value of the root node is greater than that of all nodes of the left subtree and less than that of all nodes of the right subtree, and the left subtree and the right subtree are also binary search trees. Therefore, when generating all feasible binary search trees, assuming that the current sequence length is n, if we enumerate the value of the root node as I, then according to the properties of the binary search tree, we can know that the set of node values of the left subtree is [1... I − 1], and the set of node values of the right subtree is [i+1... N], Compared with the original problem, the generation of left subtree and right subtree is a sub problem with reduced sequence length, so we can think of using backtracking method to solve this problem.
• Define the generatetrees (start,end) function to indicate that the set of current values is [start,end], and return all feasible binary search trees generated by the sequence [start,end]. According to the above idea, considering that the value I in the enumeration [start,end] is the root of the current binary search tree, the sequence is divided into [start,i − 1] and [i+1,end]. We recursively call these two parts, generatetrees (start,i - 1) and generatetrees (i+1,end), to obtain all feasible left subtrees and feasible right subtrees. In the last step, we just need to select one from the set of feasible left subtrees, then select one from the set of feasible right subtrees, splice it to the root node, and put the generated binary search tree into the answer array.
• The entry of recursion is generateTrees(1, n), and the exit is when start > end, the current binary search tree is empty, and an empty node can be returned.
• Java example:

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new LinkedList<TreeNode>();
        }
        return generateTrees(1, n);
    }

    public List<TreeNode> generateTrees(int start, int end) {
        List<TreeNode> allTrees = new LinkedList<TreeNode>();
        if (start > end) {
            allTrees.add(null);
            return allTrees;
        }

        // Enumerate possible root nodes
        for (int i = start; i <= end; i++) {
            // Obtain all feasible left subtree sets
            List<TreeNode> leftTrees = generateTrees(start, i - 1);

            // Obtain all feasible right subtree sets
            List<TreeNode> rightTrees = generateTrees(i + 1, end);

            // Select a left subtree from the left subtree set and a right subtree from the right subtree set and splice them to the root node
            for (TreeNode left : leftTrees) {
                for (TreeNode right : rightTrees) {
                    TreeNode currTree = new TreeNode(i);
                    currTree.left = left;
                    currTree.right = right;
                    allTrees.add(currTree);
                }
            }
        }
        return allTrees;
    }
}

3, Blog star help

• This year is my first time to participate in the blog star. I need the support of all leaders. In my busy schedule, take some valuable time to vote for me: https://bbs.csdn.net/topics/603955258 Give me a five-star (the list will reply one by one). Thank you very much!