This article follows the previous article. We learned about the sequential storage structure of linear tables. In this article, we learn about the chain storage structure of linear tables and compare the advantages and disadvantages of the two storage structures.
1, Lack of sequential storage structure
Although the sequential storage structure has its advantages, it also has a great defect. Its insertion and deletion need to move a large number of elements, resulting in the problem of algorithm efficiency. At present, there are few operations on the stored data, so we can't feel it. However, when the number of operations reaches a certain degree, The deficiency of the algorithm written in sequential storage structure is reflected.
2, Chain storage structure
The above sequential storage structure is insufficient. Therefore, we need a chain storage structure to solve this problem
We use an example to understand the difference between chain storage structure and sequential storage structure
Example 1
Suppose there are two zoos now. In order to make it easier for tourists to see all animals and find them, zoo A places each animal on one line, and there are the previous animal and the next animal before and after each animal; B the zoo places each animal in the most suitable position and scattered around the zoo. In order to facilitate tourists, A sign will be placed in the viewing area of each animal to recommend tourists to the next place so that tourists can see all animals. Now, the zoo wants to add A new animal. Zoo A wants to put it in the middle, but there is no position. It must move the animals in the second half back to A position; Zoo B only needs to change A sign, point the sign of the previous animal to the new animal, and then point to the next animal. Will the workload be much smaller.
Therefore, we can see that A zoo is A sequential storage structure. Its storage units are continuous. Insertion and deletion operations need to move A large number of elements, while the chain storage structure does not. Its storage space is arbitrary. It only needs to add A pointer to store the next element to each element. In this way, The later storage location does not need to be changed. This greatly reduces the execution time of the algorithm, but also increases the size of data storage. Therefore, it can be said that it sacrifices space for time.
3, Chain storage structure code (C language)
C language provides a good tool, which is pointer. We can store the location of the next data storage through pointer. Each data + pointer is called a node, the stored data is called a data field, and the place where the pointer is stored is called a pointer field.
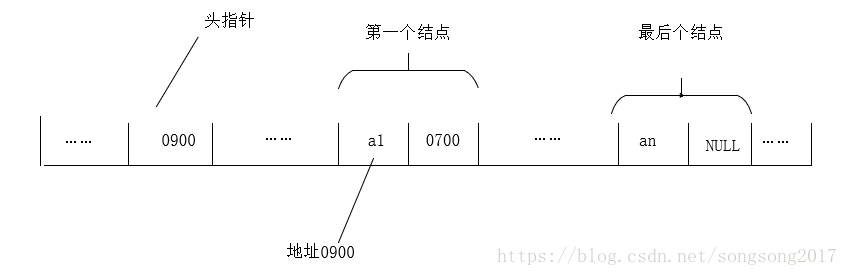
Here, you need to distinguish between the header pointer and the header node:
Header pointer:
- The head pointer refers to the pointer to the first node pointed by the linked list. If the linked list has a head node, it refers to the pointer to the head node;
- The head pointer has the function of marking, so it is often preceded by the name of the linked list
- Whether the linked list is empty or not, the header pointer is not empty. The header pointer is a necessary element of the linked list
Header node:
- The head node is set up for the unity and convenience of operation. If it is placed before the node of the first element, its data field is generally meaningless (it can also store the length of the linked list)
- With the head node, the operation of inserting and deleting the first node before the first element node is unified with other nodes
- The head node is not necessarily a necessary element of the linked list
Generally speaking, the head node is set up for easy operation, and it is OK not to use it.
Compared with the sequential storage structure, the linked list also has its disadvantages. For example, the query operation must start from the first node and point to the latter element until it is found. The time complexity is n. compared with the 1 of the sequential storage structure, it is indeed troublesome, but the insertion and deletion of the linked list will reflect its advantages over the sequential storage structure.
The figure above should clearly explain the insertion operation, that is, changing the position pointed by the pointer. Delete is the same operation, that is, point the pointer field of the previous node of the node to be deleted to the next node of the deleted node.
The following is the code (this code is the routine code in the big talk data structure, which I think has been written very clearly)
Looking at this code, I suggest reviewing the knowledge about structure and structure pointer first, because I've seen this code for a long time
#include "stdio.h"
#include "string.h"
#include "ctype.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;/* Status Is the type of function whose value is the result status code of the function, such as OK */
typedef int ElemType;/* ElemType The type depends on the actual situation. It is assumed to be int */
Status visit(ElemType c)
{
printf("%d ",c);
return OK;
}
typedef struct Node
{
ElemType data;
struct Node *next;
}Node;
typedef struct Node *LinkList; /* Define LinkList */
/* Initialize linked linear list */
Status InitList(LinkList *L)
{
*L=(LinkList)malloc(sizeof(Node)); /* Generate a header node and make L point to this header node */
if(!(*L)) /* Storage allocation failed */
return ERROR;
(*L)->next=NULL; /* Pointer field is null */
return OK;
}
/* Initial condition: linked linear list L already exists. Operation result: if l is an empty table, it returns TRUE; otherwise, it returns FALSE */
Status ListEmpty(LinkList L)
{
if(L->next)
return FALSE;
else
return TRUE;
}
/* Initial condition: linked linear list L already exists. Operation result: reset l to empty table */
Status ClearList(LinkList *L)
{
LinkList p,q;
p=(*L)->next; /* p Point to the first node */
while(p) /* It's not at the end of the watch */
{
q=p->next;
free(p);
p=q;
}
(*L)->next=NULL; /* The header node pointer field is null */
return OK;
}
/* Initial condition: linked linear list L already exists. Operation result: returns the number of data elements in L */
int ListLength(LinkList L)
{
int i=0;
LinkList p=L->next; /* p Point to the first node */
while(p)
{
i++;
p=p->next;
}
return i;
}
/* Initial condition: linked linear table l already exists, 1 ≤ i ≤ ListLength(L) */
/* Operation result: use e to return the value of the ith data element in L */
Status GetElem(LinkList L,int i,ElemType *e)
{
int j;
LinkList p; /* Declare a node p */
p = L->next; /* Let p point to the first node of the linked list L */
j = 1; /* j For counter */
while (p && j<i) /* p When it is not empty or the counter j is not equal to i, the loop continues */
{
p = p->next; /* Let p point to the next node */
++j;
}
if ( !p || j>i )
return ERROR; /* The ith element does not exist */
*e = p->data; /* Take the data of the i th element */
return OK;
}
/* Initial condition: linked linear list L already exists */
/* Operation result: returns the bit order of the first data element in L that satisfies the relationship with e. */
/* If such a data element does not exist, the return value is 0 */
int LocateElem(LinkList L,ElemType e)
{
int i=0;
LinkList p=L->next;
while(p)
{
i++;
if(p->data==e) /* Find such a data element */
return i;
p=p->next;
}
return 0;
}
/* Initial condition: linked linear table l already exists, 1 ≤ i ≤ ListLength(L), */
/* Operation result: insert a new data element e before the ith position in L, and add 1 to the length of L */
Status ListInsert(LinkList *L,int i,ElemType e)
{
int j;
LinkList p,s;
p = *L;
j = 1;
while (p && j < i) /* Find the ith node */
{
p = p->next;
++j;
}
if (!p || j > i)
return ERROR; /* The ith element does not exist */
s = (LinkList)malloc(sizeof(Node)); /* Generate a new node (C language standard function) */
s->data = e;
s->next = p->next; /* Assign the successor node of p to the successor node of s */
p->next = s; /* Assign s to the successor of p */
return OK;
}
/* Initial condition: linked linear table l already exists, 1 ≤ i ≤ ListLength(L) */
/* Operation result: delete the ith data element of L and return its value with e. the length of L is reduced by 1 */
Status ListDelete(LinkList *L,int i,ElemType *e)
{
int j;
LinkList p,q;
p = *L;
j = 1;
while (p->next && j < i) /* Traverse to find the ith element */
{
p = p->next;
++j;
}
if (!(p->next) || j > i)
return ERROR; /* The ith element does not exist */
q = p->next;
p->next = q->next; /* Assign the successor of q to the successor of p */
*e = q->data; /* Give the data in the q node to e */
free(q); /* Let the system reclaim this node to free up memory */
return OK;
}
/* Initial condition: linked linear list L already exists */
/* Operation result: output to each data element of L in turn */
Status ListTraverse(LinkList L)
{
LinkList p=L->next;
while(p)
{
visit(p->data);
p=p->next;
}
printf("\n");
return OK;
}
/* Randomly generate the values of n elements and establish a single chain linear table L with header node (header interpolation) */
void CreateListHead(LinkList *L, int n)
{
LinkList p;
int i;
srand(time(0)); /* Initialize random number seed */
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL; /* First establish a single linked list of leading nodes */
for (i=0; i<n; i++)
{
p = (LinkList)malloc(sizeof(Node)); /* Generate new node */
p->data = rand()%100+1; /* Randomly generate numbers within 100 */
p->next = (*L)->next;
(*L)->next = p; /* Insert into header */
}
}
/* Randomly generate the values of n elements, and establish a single chain linear table L with header node (tail interpolation method) */
void CreateListTail(LinkList *L, int n)
{
LinkList p,r;
int i;
srand(time(0)); /* Initialize random number seed */
*L = (LinkList)malloc(sizeof(Node)); /* L For the entire linear table */
r=*L; /* r Is the node pointing to the tail */
for (i=0; i<n; i++)
{
p = (Node *)malloc(sizeof(Node)); /* Generate new node */
p->data = rand()%100+1; /* Randomly generate numbers within 100 */
r->next=p; /* Point the pointer of the end node at the end of the table to the new node */
r = p; /* Define the current new node as the footer terminal node */
}
r->next = NULL; /* Indicates the end of the current linked list */
}
int main()
{
LinkList L;
ElemType e;
Status i;
int j,k;
i=InitList(&L);
printf("initialization L After: ListLength(L)=%d\n",ListLength(L));
for(j=1;j<=5;j++)
i=ListInsert(&L,1,j);
printf("stay L Insert the header of 1 in turn~5 After: L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n",ListLength(L));
i=ListEmpty(L);
printf("L Empty: i=%d(1:Is 0:no)\n",i);
i=ClearList(&L);
printf("empty L After: ListLength(L)=%d\n",ListLength(L));
i=ListEmpty(L);
printf("L Empty: i=%d(1:Is 0:no)\n",i);
for(j=1;j<=10;j++)
ListInsert(&L,j,j);
printf("stay L Insert 1 at the end of the table~10 After: L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n",ListLength(L));
ListInsert(&L,1,0);
printf("stay L After the header of is inserted into 0: L.data=");
ListTraverse(L);
printf("ListLength(L)=%d \n",ListLength(L));
GetElem(L,5,&e);
printf("The value of the fifth element is:%d\n",e);
for(j=3;j<=4;j++)
{
k=LocateElem(L,j);
if(k)
printf("The first%d The values of the elements are%d\n",k,j);
else
printf("No value is%d Element of\n",j);
}
k=ListLength(L); /* k Table length */
for(j=k+1;j>=k;j--)
{
i=ListDelete(&L,j,&e); /* Delete the j-th data */
if(i==ERROR)
printf("Delete paragraph%d Data failed\n",j);
else
printf("Delete paragraph%d The element values of are:%d\n",j,e);
}
printf("Sequential output L Elements:");
ListTraverse(L);
j=5;
ListDelete(&L,j,&e); /* Delete the 5th data */
printf("Delete paragraph%d The element values of are:%d\n",j,e);
printf("Sequential output L Elements:");
ListTraverse(L);
i=ClearList(&L);
printf("\n empty L After: ListLength(L)=%d\n",ListLength(L));
CreateListHead(&L,20);
printf("Overall creation L Element of(Head insertion): ");
ListTraverse(L);
i=ClearList(&L);
printf("\n delete L After: ListLength(L)=%d\n",ListLength(L));
CreateListTail(&L,20);
printf("Overall creation L Element of(Tail interpolation): ");
ListTraverse(L);
return 0;
}
4, Chained storage structure of linear list (Java)
Because Java does not have the concept of pointer variable or structure, we will use class to replace the structure, and the pointer address is actually the object name. We can define a node class to store the next node.
Then the idea is: we define a Node class Node as a Node. The Node class has a data field and a pointer field. The pointer field is implemented by Node next. This pointer is actually a class. Define the linked list class, which contains the head pointer and tail pointer, as well as the operations on the linked list. It generizes the linked list and can store any object.
The following code is written by myself. There may be some shortcomings and the encapsulation is not very good. As for the operation of deletion and insertion, it is actually the same as C language. You can see the above.
package date;
public class LinkedList<E>{
private Node head;//Head node of linked list
private Node rear;//Tail pointer of linked list
private int size=0;
private class Node{//Node class
E data;//Data domain
Node next;//Pointer field
public Node(){
this.data=null;
this.next=null;
}
public Node(E e){
this.data=e;
this.next=null;
}
public Node(E e,Node next){
this.data=e;
this.next=next;
}
}
public LinkedList() {//The tail pointer is null, and the head pointer points to the tail pointer to create a linked list
this.head=new Node();
this.rear=null;
}
public void add(int index, E e) {
if(index<0 || index>size){
throw new IllegalArgumentException("Angle mark out of bounds");
}
Node n = new Node(e);
if(size==0){
head.next = n;
rear = n;
}else if(index ==0){ //Head insertion
n.next = head.next;
head.next = n;
}else if(index == size){ //Tail interpolation
rear.next = n;
rear = n;
}else{ //Intermediate insertion
Node p = head;
for (int i = 0; i < index; i++) {
p = p.next;
}
n.next = p.next;
p.next = n;
}
this.size++;
}
public E remove(int index) {
if(size==0){
throw new IllegalArgumentException("Empty table");
}
if(index<0 || index>=size){
throw new IllegalArgumentException("Angle mark out of bounds");
}
E res = null;
if(size == 1){//When there is only one data
res = head.next.data;
head.next = null;
rear = head;
}else if(index == 0){
Node del = head.next;
res = del.data;
head.next = del.next;
del.next = null;
del = null;
}else if(index == size-1){
Node p = head;
while(true){
if(p.next != rear){
p = p.next;
}else{
break;
}
}
res = p.next.data;
p.next = null;
rear = p;
}else{
Node p = head;
for (int i = 0; i < index; i++) {
p = p.next;
}
Node del = p.next;
res = del.data;
p.next = del.next;
del.next = null;
del = null;
}
size--;
return res;
}
public E get(int index) {
if(size==0){
throw new IllegalArgumentException("Empty table");
}
if(index<0 || index>size){
throw new IllegalArgumentException("Angle mark out of bounds");
}
if(index == 0){
return head.next.data;
}else if(index == size-1){
return rear.data;
}else{
Node p = head;
for (int i = 0; i <= index; i++) {
p = p.next;
}
return p.data;
}
}
public static void main(String[] args) {
LinkedList s=new LinkedList();
for(int i=0;i<5;i++)
{
s.add(i, i);
}
System.out.println("List length:"+s.size);
System.out.println("2nd data:"+s.get(2));
System.out.println("Delete the second data");
s.remove(2);
for(int i=0;i<s.size;i++)
{
System.out.println("output"+s.get(i));
}
}
}
5, Static linked list
- Why do you need a static linked list: C language can well operate the data in memory through the pointer, and Java also realizes the function of the pointer through the object reference mechanism, but the early languages such as Basic can not realize this function, so how to realize the linked list? That is to use arrays to describe linked lists.
- How to realize the static linked list: we know that each node needs a pointer field and data field. In C language, we also use the structure to realize the pointer field, but at this time, we do not use the structure pointer to realize it, and define an int variable as a cursor. We use the array as a linked list to store these structures, and the cursor is the subscript pointing to the position where the next structure is stored in the array. In this way, we can realize the linked list without using pointer variables.
Although the static linked list implements the linked list and solves the element movement problem of the sequential storage structure. It only needs to modify the cursor, it loses the random access characteristics of the linked storage structure because it uses an array for description. Therefore, the use of static linked list is not widely used in C language and Java, and it is not recommended.
So there is no code here. You can try. It will be easier to understand if you describe it with an array.
6, Circular linked list and bidirectional linked list
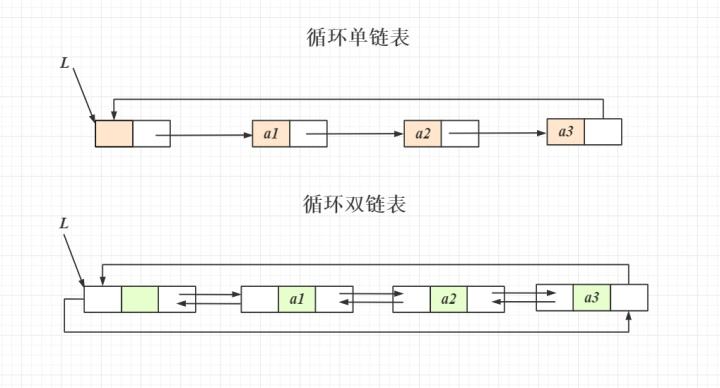
In fact, there is nothing special about these two linked lists. The circular linked list connects the first node and the tail node. The two-way linked list is the pointer field stored by the node. We call it the parent node and the child node for the time being. The parent node is the pointer to the previous node and the child node is the pointer to the next node. In this way, when we search, You can conduct a two-way search.

Understand the single linked list, then whether it is a circular linked list, a two-way linked list, or a circular two-way linked list, it is actually the same. What we need to understand is the basic concept and storage mode of the linked list.