1. Running training
Problem Description:
Xiao Ming wants to do a running training. At the beginning, Xiao Ming is full of physical strength, and the physical strength value is 10000.
If Xiao Ming runs, he will lose 600 physical strength per minute.
If Xiao Ming has a rest, he will increase his physical strength by 300 per minute.
The loss and increase of physical strength vary evenly.
Xiao Ming plans to run for one minute, rest for one minute, run for another minute, rest for another minute... This cycle.
If Xiaoming's physical strength reaches 0 at a certain time, he will stop exercising. How long will Xiaoming stop exercising.
In order to make the answer an integer, please output the answer in seconds. Only the number, not the unit, is filled in the answer.
Answer submission:
This is a result filling question. You just need to calculate the result and submit it.
The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
Solution:
Idea:
1. End condition: physical strength = 0.
2. Time accumulation. Physical strength is calculated according to state.
3. Since the result is in seconds, remember to convert.
code:
Although this is a result filling question, since it is an assignment, we might as well solve it with code
# encoding:utf-8
# @Author : fyl
time = 0
power = 10000
while power > 0:
time += 1
if time % 2 == 0:# Judge the status in the past 1 minute
power += 300
else:
power -= 600
if power == 0:
time = time*60
else:
#The last minute must be running, which may cause the power to be less than 0
time = (time-1)*60 + ((power+600)/600)*60 #Make up the last minute. power is converted into seconds in proportion.
time = int(time) #Because the result of this problem only writes this integer, type conversion is carried out
print(time)
Operation result: 3880
Summary:
There is a small trap in this question: after the last minute of running, power is negative, that is, power cannot be reduced to 0 after a whole minute of exercise. We'll calculate the last minute separately.
2. Factorial divisor
Problem Description:
Define factorial n= one × two × three × ··· × n.
Excuse me 100! (factorial of 100) how many divisors are there.
Answer submission:
This is a question to fill in the blanks. You just need to calculate the results and submit them.
The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
Solution:
Idea:
100! It's a huge number. Violent solution must not work. We can decompose 1 ~ 100 factors respectively, and multiply these factors to get 100! Factorization of.
Approximate number:
Any positive integer n greater than 1 can be decomposed into prime factors: p1a1p2a2... pkak
Where pi is two different prime numbers and ai is the corresponding index, then the number of divisors of n is (a1+1)(a2+1)... (ak+1)
code:
# encoding:utf-8
# @Author : fyl
dic={}
for i in range(2,101): #Dictionary dic is used to count the number of factors of these 100 numbers. The initialization value is 0
dic[i] = 0
for i in range(2,101): #Cycle 2 ~ 100 to find their quality factor and count the quantity
n=i
while n!=1:
for p in range(2,n+1):
if n % p == 0:
dic[p]+=1
n = n//p
break
res = 1
for k in arr.keys(): #The number of divisors is (a ~ 1 ~ + 1) * (a ~ 2 ~ + 1) ** (a~k~+1)
res *= dic[k]+1
print(res)
Operation result: 39001250856960000
Summary:
This question involves counting the quantity, which needs to be counted with a dictionary. Also have some mathematical knowledge of divisor.
3. Stack order
Problem Description:
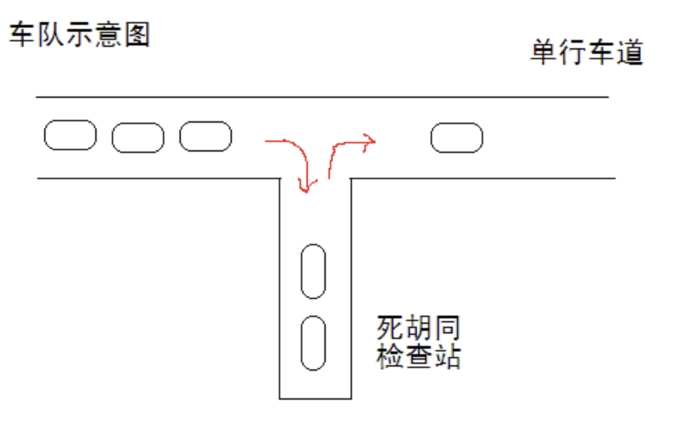
Planet X pays special attention to order. All roads are one-way streets.
A fleet of 16 beetles started successively according to the number, caught in other traffic flows and moved forward slowly.
There is a dead end on the roadside, which can only allow one car to pass. It is a temporary checkpoint, as shown in the figure.
Planet X is so rigid that every passing car is required to enter the checkpoint, or it may be released without inspection, or it may be carefully inspected.
If the order of vehicles entering and leaving the checkpoint can be staggered arbitrarily.
So, how many possible orders will the team take when it gets on the road again?
For convenience, it is assumed that the checkpoint can accommodate any number of cars.
Obviously, if the fleet has only one vehicle, there may be one order; 2 possible sequences of 2 vehicles; There are 5 possible sequences for 3 vehicles.
There are 16 cars now, pro! You need to calculate the number of possible orders.
Answer submission:
This is an integer. Please submit the answer through the browser and do not fill in any redundant content (such as explanatory text).
Solution:
Idea:
Recursion is adopted, and recursion is considered in three cases
1. When there are no cars on the left side of the lane, there is only one order regardless of whether there are cars in the checkpoint. This is the baseline condition return 1.
2. When there are cars on the left and there are no cars in the checkpoint, according to the requirements of the topic, each car must enter the checkpoint, so the number of cars on the left - 1, the number of cars in the checkpoint + 1 return f (n-1,1).
3. If there are cars in the checkpoint, the number of schemes in this case is the sum of two recursions. The two recursions correspond to: another car on the left enters the checkpoint and another car out of the checkpoint return f (n - 1,m + 1) + f (n,m - 1).
code:
# encoding:utf-8
def fun(n,m):#n is the number of vehicles on the left, and m is the number of vehicles in the checkpoint
if n == 0:#If there's no car on the left
return 1
if m == 0:#If there is no car at the checkpoint, enter the checkpoint
return fun(n-1,1)
if m > 0:#If there is a car at the checkpoint
#There are two cases: 1 Another car on the left comes in 2 A car went out of the checkpoint
return fun(n-1,m+1) + fun(n,m-1)
print(fun(16,0))
Reference link: https://blog.csdn.net/qq_45281807/article/details/104221946
Another solution idea: the number of stack order is Cartland number, which satisfies a recursive formula: h1=1; hn=hn-1(4n-2)/(n+1). Where n represents the number of numbers.
# encoding:utf-8
ans = 1
for x in range(1, 17):
ans = ans*(4*x-2)/(x+1)
print(ans)
Reference link: https://blog.csdn.net/milk_paramecium/article/details/113893758
Operation result: 357670
Summary:
When using recursive methods, you must find the baseline conditions and recursive conditions.
4. Goldbach decomposition
Problem Description:
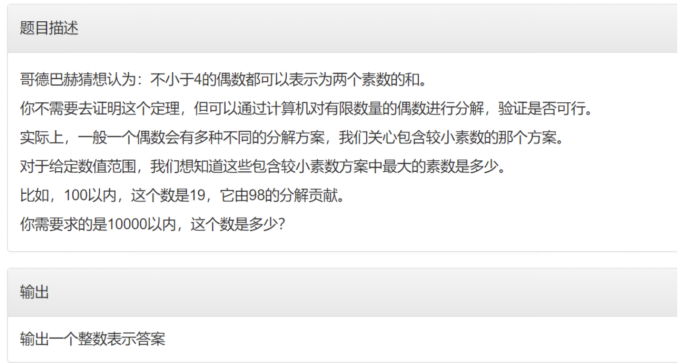
Solution:
Idea:
Each even number is decomposed into two prime numbers, as long as the smallest one, and then find the largest one in this range. The even number range of this question is within 10000.
code:
# encoding:utf-8
x = []
def Split_even(n):#Defines a function that decomposes even numbers
def IsPrime(num): #Determine whether num is a prime number
if num == 2:
return True
for i in range(2,num):
if num % i == 0:
return False
return True
for j in range(2, n // 2 + 1):
if IsPrime(j) and IsPrime(n - j):#Judge whether these two numbers are prime numbers
return [j,n-j]# If both are, the two prime numbers are returned
for i in range(4,10001,2):
x.append(min(Split_even(i)))#Add the smallest of the decomposed two prime numbers to the x list
print(max(x))#Print the largest element in the list
Operation result: 173
5. Book arrangement
Problem Description:
10 books numbered 1 ~ 10 shall be placed on the bookshelf, and the books with adjacent numbers shall not be placed in adjacent positions.
Please calculate how many different permutations there are.
Answer submission:
What needs to be submitted is an integer. Do not fill in any redundant content.
Solution:
Idea:
1. Find out all possible permutations (full permutations).
There are n elements in the list. Fix the first element and fully arrange the remaining n - 1 elements.
Exchange the first element with other elements, and fully arrange the remaining n-1 elements after each exchange.
The remaining n - 1 elements are arranged completely, as above. After fixing, arrange n - 2.
Until the number of arrays is 1, the full permutation is itself, completing one permutation.
2. Then judge whether these permutations comply with "the books with adjacent numbers are not in the adjacent position", and count the permutations that comply.
code:
# encoding:utf-8
res = 0
def check(book):#Check whether the "book with adjacent number is not in adjacent position" is met and count
for i in range(9):
if abs(book[i]-book[i+1]) == 1:
return False
return True
def Full_Perm(book, begin, end):
global res#The variables inside the function and outside the function should be declared with global
if begin == end:#Recursive end condition. When the last element is exchanged, there is no need to exchange again. This arrangement is completed.
if check(book):
res += 1
return
else:
j = begin
for i in range(begin, end):#Full Permutation from begin to end
book[i],book[j] = book[j],book[i]#exchange
Full_Perm(book, begin+1, end)# After the exchange, the remaining arrays are fully arranged. [begin + 1, end]
book[i],book[j] = book[j],book[i] #Restore to the state before the exchange for the next exchange
book = [i for i in range(1, 11)]
Full_Perm(book, 0, len(book))
print(res)
Operation result: 479306
Summary:
The key point of this problem is to write a recursive function to realize full permutation.
Python itertools library has functions to implement full permutation.
# encoding:utf-8 import itertools s = ['a','b','c'] for i in itertools.permutations(s): print(i)
6. Monkeys divide bananas
Problem Description:

Solution:
Idea:
code:
# encoding:utf-8
n=6#Set the initial value of the number of bananas the first monkey sees when waking up to at least 6
a=b=c=d=0
while True:
if(n%5==1):#Meet the condition that the first monkey has one banana left
a=(n-1)/5*4#The number of bananas the second monkey saw when he woke up
if(a%5==2):
b=(a-2)/5*4#The number of bananas the third monkey saw when he woke up
if(b%5==3):
c=(b-3)/5*4#The number of bananas the fourth monkey saw when he woke up
if(c%5==4):
d=(c-4)/5*4#The number of bananas the fifth monkey saw when he woke up
if(d%5==0 and d!=0):#Judge whether it meets the condition that the fifth monkey divides bananas equally and just finished
print(n)
break
n+=1
Reference link: https://blog.csdn.net/qq_40871196/article/details/86690969
Summary:
Didn't figure out how to solve it recursively. It doesn't seem to use recursion,
7. Slightly smaller score
Problem Description:
Back to primary school----
True fraction: fraction whose numerator is less than denominator
Reduced fraction: the coprime of numerator and denominator, that is, the maximum common divisor is 1
The entrance verification method of Planet x math city is:
A true score is displayed on the screen. You need to quickly find a reduced score smaller than it. The larger the score, the better.
At the same time, limit the denominator of your score to no more than 100.
Solution:
Idea:
code:
# encoding:utf-8
def gcd(a,b):
if b==0:
return a
return gcd(b,a%b)
#This is the score a/b displayed on the screen
a = 7
b = 13
max_a = 0
max_b = 1
for n in range(100,1,-1):
for m in range(n-1,0,-1):
if (m*b<a*n) and (gcd(m,n) == 1):
if max_a*n < max_b*m:
max_a = m
max_b = n
break
print("%d/%d"%(max_a, max_b))
Summary:
This question is a blank filling question in the original question of Blue Bridge Cup. Since the input format is not specified in the assignment, the input cannot be controlled, and the original question is copied directly.
8.excel address
Problem Description:
Time limit: 1.0s memory limit: 256.0MB
Problem Description:
The address representation of Excel cells is very interesting. It uses letters to represent column numbers.
For example,
A stands for column 1,
B represents column 2,
Z represents column 26,
AA means column 27,
AB stands for column 28,
BA stands for column 53,
...
Of course, the maximum column number of Excel is limited, so it is not difficult to convert.
If we want to generalize this representation, can we convert large numbers into long letter sequences?
This topic is to output the corresponding Excel address representation of the input number.
sample input
26
sample output
Z
sample input
2054
sample output
BZZ
Data scale and agreement
We agree that the input integer range [12147483647]
Peak memory consumption (including virtual machine) < 256M
CPU consumption < 1000ms
Please output in strict accordance with the requirements, and do not print superfluous contents such as "please input...".
be careful:
The main function needs to return 0;
Only ANSI C/ANSI C + + standards are used;
Do not call special functions that depend on the compilation environment or operating system.
All dependent functions must be explicitly #include in the source file
Common header files cannot be omitted through project settings.
When submitting programs, pay attention to selecting the desired language type and compiler type.
Solution:
Idea:
The problem is similar to the conversion from hexadecimal to hexadecimal, but it is only similar. We can solve it by recycling surplus.
code:
# encoding:utf-8
n = int(input())
ans = []
while n!= 0:
if n % 26 == 0:
ans.append(26)
n = n // 26 - 1 # here - 1 is required
else:
ans.append(n%26)
n = n // 26
for i in range(len(ans)):
#Add 64 to convert numbers into characters and print forward from the end of the list
print(chr(ans[len(ans)-i-1]+64), end='')
Reference link: https://blog.csdn.net/qq_43604482/article/details/105825981
Summary:
Note that it is not really binary 26. For example, it is Z and AZ at points 26 and 52. It is not carried like the real hexadecimal, but needs to add 1 to complete the carry. Therefore, a carry is subtracted from the multiple node of 26.
9. Date issue
Problem Description:
Xiao Ming is sorting out a batch of historical documents. Many dates appear in these historical documents. Xiao Ming knows that these dates are from January 1, 1960 to December 31, 2059. What bothers Xiao Ming is that the formats of these dates are very different, including year / month / day, month / day / year and day / month / year. What is more troublesome is that the first two digits of the year are omitted, so that there are many possible dates corresponding to a date in the literature.
For example, 02 / 03 / 04 may be March 4, 2002, February 3, 2004 or March 2, 2004.
Given a date in the literature, can you help Xiao Ming judge which possible dates correspond to it?
input
A date in the format "AA/BB/CC". (0 <= A, B, C <= 9)
output
Output several different dates, one line for each date, in the format of "yyyy MM DD". Multiple dates are arranged from morning to night.
sample input
02/03/04
sample output
2002-03-04
2004-02-03
2004-03-02
Resource agreement:
Peak memory consumption (including virtual machine) < 256M
CPU consumption < 1000ms
Solution:
Idea:
Consider the unsatisfied situation comprehensively, and finally sort and de duplicate.
code:
# encoding:utf-8
data = list(map(int, input().split("/")))
res = []
def isLeapYear(year):
if (year % 4 == 0 and year % 100 != 0) or year % 400 == 0:
return True
else:
return False
def fun(x, y, z): # Default date
if 0<=x<=59: #Year of discussion
x += 2000
elif 60<=x<=99:
x += 1900
if y <= 0 or y > 12:#Discussion month
return False
if z <= 0 or z > 31:#Discussion day
return False
if isLeapYear(x) and y == 2 and z > 29:
return False
if isLeapYear(x) == False and y == 2 and z > 28:
return False
if y in [4,6,9,11] and z > 30:
return False
else:
if y < 10:
y = str(0) + str(y)
if z < 10:
z = str(0) + str(z)
res.append(str(x) + "-" + str(y) + '-' + str(z))
return
fun(data[0], data[1], data[2])#a[0] is the year, a[1] is the month, and a[2] is the day
fun(data[2], data[0], data[1])#a[0] is the month, a[1] is the day, and a[2] is the year
fun(data[2], data[1], data[0])#a[0] is the day, a[1] is the month, and a[2] is the year
for i in sorted(list(set(res))):
print(i)
Reference link: https://blog.csdn.net/bianxia123456/article/details/106816421
Summary:
10. Integer division
Problem Description:
The division of a positive integer n is the expression that turns n into the sum of a series of positive integers. Note that the partition has nothing to do with the order, for example, 6 = 5 + 1 It is the same partition as 6 = 1 + 5. In addition, the integer itself is also a partition.
For example, for a positive integer n=5, it can be divided into:
1+1+1+1+1
1+1+1+2
1+1+3
1+2+2
2+3
1+4
5
Enter description
Enter a positive integer n
Output description
Output the total number of n integer partitions k
sample input
5
sample output
7
Solution:
Idea:
Each of the above numbers is defined as the division factor of 6. It can be seen that 6 has 6 division factors, and each of them may form 6. You can then use a for loop to traverse the partition factors in turn. For example, starting from 1, 1 is the first number to form 6, then rest = 6-1 Then do the same analysis for rest, that is, recursion. The recursive termination condition is that when rest = 0, 6 is divided and output. At this time, a data structure is needed to store the appropriate partition factor and traverse the output from here. Finally, in order to remove duplication, an if judgment is added during backtracking after recursion. It is specified that the partition factor stored in the data structure can be stored only when it is judged that the partition factor is not less than the previous bit (subscript-1) before storing a new partition factor.
code:
# Use the python dictionary data structure to store the partition factor, starting from 1 and occupying the bit with 0
dividing_number = {0: 0}
# Number accumulation variable
times = 0
def int_divide(number, index):
global times
# Traverse all partition factors of the integer starting from 1
for i in range(1, number+1):
# Compared with the previous division factor, the weight can be removed. If there are 24 and 42 first, it will not work
if i >= dividing_number[index-1]:
dividing_number[index] = i
# Current number - the number remaining after dividing the factor, such as 6-1 and 5
number_rest = number - i
# The integer is divided
if number_rest == 0:
# Output partition factor
for j in range(1, index):
print(str(dividing_number[j])+'+', end='')
print(str(dividing_number[index]))
times = times + 1
# Not divided, continue, dividing_Number division digit + 1
else:
int_divide(number_rest, index+1)
else:
pass
n = int(input("Please enter an integer\n"))
int_divide(n, 1)
print("Therefore, the partition number of this integer is:%d" % times)
Reference link: https://blog.csdn.net/qq_42980666/article/details/105037553
Summary:
The problem is solved skillfully by recursion, which not only completes the division of factors, but also avoids repeated ideas. It's good to learn.
11. One step away
Problem Description:
Waking up from a coma, Xiao Ming finds himself locked up in a waste mine truck on Planet X.
The mine car stopped on a flat abandoned track.
In front of him were two buttons, which read "F" and "B".
Xiao Ming suddenly remembered that these two buttons can control the mine car to move forward and backward on the track.
Press F to advance 97 meters. Pressing B will move back 127 meters.
Through the dim light, Xiao Ming sees a monitoring probe 1 meter in front of him.
He had to try to stop the harvester right under the camera before he had a chance to get help from his companions.
Perhaps it can be done by multiple operations F and B.
The power on the mine car is not enough, and the yellow warning light is flashing silently
Each F or B operation will consume a certain amount of energy.
Xiao Ming quickly calculated how many operations it would take to park the mine car exactly one meter ahead.
Please fill in the minimum number of operations required to achieve the goal.
Note that what needs to be submitted is an integer. Do not fill in any irrelevant content (such as explanation, etc.)
Solution:
Idea:
According to the meaning of the question, the equation can be listed: 97x - 127y = 1. The answer can be found through violent enumeration
code:
# encoding:utf-8
for x in range(0,1000):
for y in range(0,1000):
if 97 * x - 127 * y == 1:
print(x + y)
break
else:
continue
break
Summary:
The scope of enumeration can be written larger, and the for else statement can be used to jump out of the double-layer loop. You can also set a global variable flag to jump out of multi-layer loops, such as:
# encoding:utf-8
flag = False
for x in range(0,1000):
for y in range(0,1000):
if 97 * x - 127 * y == 1:
print(x + y)
flag = True
break
if flag:
break
12. Robot tower
Problem Description:
The robot show cheerleaders on Planet X have two kinds of clothes, A and B.
Their performance this time is to build a robot tower.
similar:
A
B B
A B A
A A B B
B B B A B
A B A B B A
The tower rules in the team are:
A can only stand on the shoulders of AA or BB.
B can only stand on the shoulders of AB or BA.
Your task is to help cheerleaders calculate how many kinds of towers can be formed when given the number of A and B.
Enter two integers M and N in one line, with spaces separated (0 < M, n < 500), representing the number of people in A and B respectively, so as to ensure the rationality of the number of people.
It is required to output an integer indicating the number of patterns that can be generated.
For example:
User input:
1 2
The program should output:
3
Another example:
User input:
3 3
The program should output:
4
Resource agreement:
Peak memory consumption < 256M
CPU consumption < 1000ms
Solution:
Idea:
cnt = num*(num+1)/2 = M+N, so num = sqrt((M + N) * 2)
The next step is to find the bottom layer, and then check whether it can be expanded upward and whether the number of A and B is enough.
Here, we iterate through all the options in the first row, using A recursive method, with 1 for A and 2 for B.
Then set A check code and calculate the number of all A, B and N from the line. If it is the same as m and N at the top level, it indicates that it is feasible.
code:
# encoding:utf-8
import math
def check():# Judge whether it can expand upward
a = 0
b = 0
tmp = row
while tmp >0:
for i in range(1, tmp+1):
if cnt[i] == 1:
a +=1
else:
b += 1
for i in range(2, tmp+1):
if cnt[i-1]==cnt[i]:
cnt[i-1] = 1
else:
cnt[i-1] = 2
tmp -=1
if a == m and b == n:
return True
else:
return False
def dfs(k):# Traverse all underlying
global res
if k > row:
if check():
res +=1
return
cnt[k] = 1
dfs(k+1)
cnt[k] = 2
dfs(k+1)
if __name__ == "__main__":
m = int(input())
n = int(input())
res = 0
cnt = [0 for _ in range(100010)]
row = int(math.sqrt(2*(m+n)))
dfs(1)
print(res)
Reference link: https://blog.csdn.net/zznnniuu/article/details/122352199
13. Fill in the blanks with seven stars
Problem Description:
As shown in the figure below. Fill in the number 1 ~ 14 on the 14 nodes of the seven pointed star without repetition or omission. The sum of the four numbers on each line must be equal.
Picture description
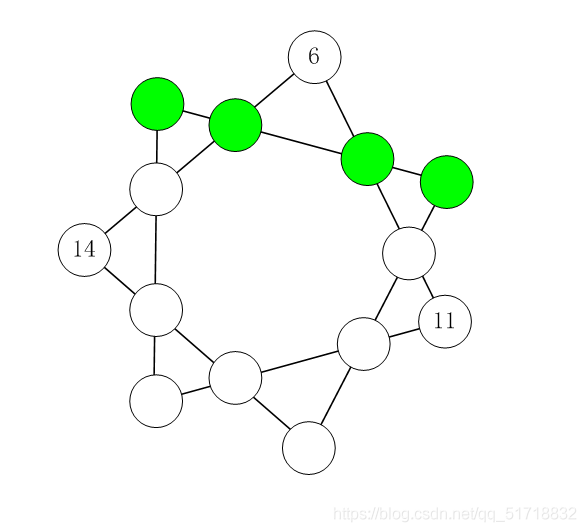
Three numbers have been given in the figure. Please calculate the number to be filled in other places. The answer is unique.
After filling in, please output 4 numbers of the green node (from left to right, separated by spaces).
Solution:
Idea:
Use python full permutation function to traverse all. Write the subscript on the graph and use the if statement to judge the seven lines.
code:
# encoding:utf-8
import itertools
for i in itertools.permutations([1,2,3,4,5,7,8,9,10,12,13]):
num=i[0]+i[1]+i[2]+i[3]
if num==i[3]+i[5]+i[7]+i[10]:
if num==i[10]+i[9]+i[6]+14:
if num==14+i[4]+i[1]+6:
if num==6+i[2]+i[5]+11:
if num==11+i[7]+i[9]+i[8]:
if num==i[8]+i[6]+i[4]+i[0]:
print(i[0],i[1],i[2],i[3])
break
Operation result: 10 3 9 8