Today, let's learn about the application of stack and stack, and learn the application of stack in recursive algorithm and four arithmetic expressions
1, Definition of stack
Everyone should have encountered an exception called "stack overflow" when writing a program. What are the similarities and differences between this stack and the stack we are going to learn today?
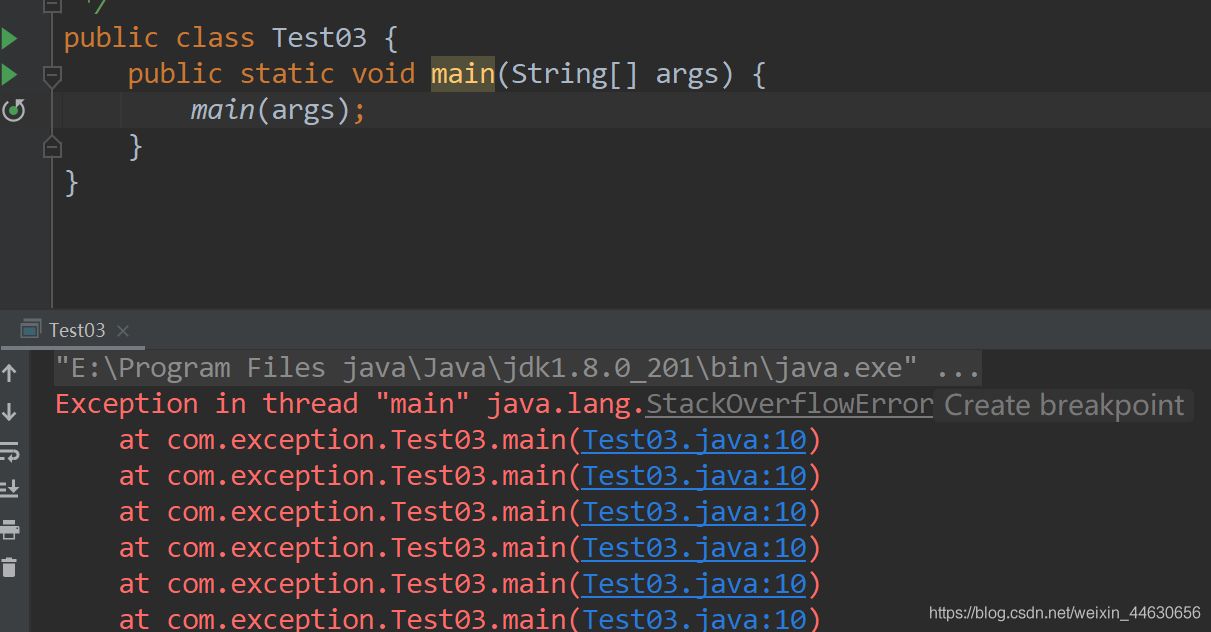
Stack overflow is a kind of buffer overflow.
Due to buffer overflow, useful storage units are overwritten, which often leads to unpredictable consequences. In order to temporarily access data during the operation of a program, some memory space is generally allocated, which is usually called buffer. If more data than its own length is written to the buffer, so that the buffer cannot be accommodated, the storage units outside the buffer will be overwritten. This phenomenon is called buffer overflow. The buffer} length is generally related to the type of buffer variable defined by the user. Stack overflow is a kind of buffer overflow.
The stack we want to learn today is a data storage structure, which means that when storing and deleting data, you can only add and delete data at the top of the stack
Definition of stack: stack is a linear table that is limited to insert and delete operations only at the end of the table.
2, Abstract data type of stack
ADT Stack {
Data object:
D = {ai | ai ∈ ElemSet,i = 1,2,3,....,n, n ≥ 0} // ElemSet represents a collection of elements
Data relationship:
R1={<ai-1, ai> | ai-1 , ai∈D,i=2,...,n} // ai-1 is the precursor and ai is the successor
appointment an The end is the top of the stack, a1 The end is the bottom of the stack
Basic operations: initialization, stack entry, stack exit, stack top element fetching, etc
} ADT Stack
InitStack(&S)Initialization operation
Operation result: construct an empty stack S
DestroyStack(&S)Destroy stack operation
Initial condition: stack S Already exists
Operation result: stack S Destroyed
StackEmpty(S)Determine whether the stack is empty
Initial condition: stack S Already exists
Operation result: if stack S If the stack is empty, return TRUE,
If stack S If it is not empty, return FALSE.
StackLength(S)Find the length of the stack
Initial condition: stack S Already exists
Operation result: return stack S The number of elements, that is, the length of the stack
GetTop(S,&e)Get stack top element
Initial condition: stack S Already exists and is not empty
Operation result: use e return S Stack top element
ClearStack(&S)Stack command operation
Initial condition: stack S Already exists
Operation result: Set S Clear to empty stack
Push(&S,e)Stack operation
Initial condition: stack S Already exists
Operation result: insert element e For the new stack top element
Pop(&S,&e)Out of stack operation
Initial condition: stack S Exists and is not empty
Operation result: delete stack SD Stack top element an,Combined use e Returns its value
3, Sequential storage structure of stack (C language, Java)
We have learned about the sequential storage structure in the linear table. The stack is also a special linear table, but it can only be inserted and deleted at the top of the stack, while other operations, such as search, do not have this restriction. Therefore, there is not much difference between the implementation of the stack and the implementation of the linear table.
For sequential storage structures, arrays can be used. We take the elements of the 0 corner of the array as the bottom of the stack, which is convenient for us to store. Here, you only need to add a top variable to identify the top element of the stack.
The code is basically similar to that of a linear table, except that insertion and deletion are different. However, you can understand that insertion and deletion can be performed at the end of a linear table.
I think the linear table should be easy to understand
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int SElemType; /* SElemType The type depends on the actual situation. It is assumed to be int */
/* Sequential stack structure */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* Pointer for stack top */
}SqStack;
Status visit(SElemType c)
{
printf("%d ",c);
return OK;
}
/* Construct an empty stack S */
Status InitStack(SqStack *S)
{
/* S.data=(SElemType *)malloc(MAXSIZE*sizeof(SElemType)); */
S->top=-1;
return OK;
}
/* Set S to empty stack */
Status ClearStack(SqStack *S)
{
S->top=-1;
return OK;
}
/* If stack S is an empty stack, it returns TRUE; otherwise, it returns FALSE */
Status StackEmpty(SqStack S)
{
if (S.top==-1)
return TRUE;
else
return FALSE;
}
/* Returns the number of elements of S, that is, the length of the stack */
int StackLength(SqStack S)
{
return S.top+1;
}
/* If the stack is not empty, use e to return the top element of S and return OK; Otherwise, ERROR is returned */
Status GetTop(SqStack S,SElemType *e)
{
if (S.top==-1)
return ERROR;
else
*e=S.data[S.top];
return OK;
}
/* Insert element e as the new stack top element */
Status Push(SqStack *S,SElemType e)
{
if(S->top == MAXSIZE -1) /* Stack full */
{
return ERROR;
}
S->top++; /* The stack top pointer is increased by one */
S->data[S->top]=e; /* Assign the newly inserted element to the stack top space */
return OK;
}
/* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
Status Pop(SqStack *S,SElemType *e)
{
if(S->top==-1)
return ERROR;
*e=S->data[S->top]; /* Assign the stack top element to be deleted to e */
S->top--; /* Stack top pointer minus one */
return OK;
}
/* Each element in the stack is displayed from the bottom of the stack to the top of the stack */
Status StackTraverse(SqStack S)
{
int i;
i=0;
while(i<=S.top)
{
visit(S.data[i++]);
}
printf("\n");
return OK;
}
int main()
{
int j;
SqStack s;
int e;
if(InitStack(&s)==OK)
for(j=1;j<=10;j++)
Push(&s,j);
printf("The elements in the stack are:");
StackTraverse(s);
Pop(&s,&e);
printf("Pop up stack top element e=%d\n",e);
printf("Stack empty No:%d(1:Null 0:no)\n",StackEmpty(s));
GetTop(s,&e);
printf("Stack top element e=%d Stack length is%d\n",e,StackLength(s));
ClearStack(&s);
printf("Empty stack after emptying stack No:%d(1:Null 0:no)\n",StackEmpty(s));
return 0;
}
After reading the C language version of the stack in the book, let's write the Java version of the stack ourselves
package Text;
public class Stack {
private int top = -1;
private final int DEFAULT_SIZE = 6;
private String[] arr = new String[DEFAULT_SIZE];
public boolean push(String value) {
if(top == arr.length -1) {
return false;
}
++top;
arr[top] = value;
return true;
}
public boolean pop() {
if(top == -1) {
return false;
}
String temp = arr[top];
top--;
return true;
}
public boolean isEmpty() {
return top == -1;
}
public String getTop() {
if(top == -1) { //Stack is empty
return null;
}
return arr[top];
}
public static void main(String[] args) {
Stack stack = new Stack();
System.out.println(stack.isEmpty());
stack.push("abc"); // Enter the stack
stack.push("def");
stack.push("ggg");
System.out.println(stack.isEmpty());
System.out.println(stack.getTop());
System.out.println(stack.pop()); // Out of stack
System.out.println(stack.getTop()); // Get stack top element
}
}
4, Chain storage structure of stack (C language, Java)
It's the same. It's similar to the chain storage structure of a linear table, except that the pointer variable here does not point to the next element, but refers to the previous element until the first element. The pointer field of the first element is empty. As for the stack operation, it's very simple. Just point the top pointer to the lower element of the element to be deleted, Then release the memory of the stack top element to be deleted. Upper code
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 / * initial allocation of storage space*/
typedef int Status;
typedef int SElemType; /* SElemType The type depends on the actual situation. It is assumed to be int */
/* Chain stack structure */
typedef struct StackNode
{
SElemType data;
struct StackNode *next;
}StackNode,*LinkStackPtr;
typedef struct
{
LinkStackPtr top;
int count;
}LinkStack;
Status visit(SElemType c)
{
printf("%d ",c);
return OK;
}
/* Construct an empty stack S */
Status InitStack(LinkStack *S)
{
S->top = (LinkStackPtr)malloc(sizeof(StackNode));
if(!S->top)
return ERROR;
S->top=NULL;
S->count=0;
return OK;
}
/* Set S to empty stack */
Status ClearStack(LinkStack *S)
{
LinkStackPtr p,q;
p=S->top;
while(p)
{
q=p;
p=p->next;
free(q);
}
S->count=0;
return OK;
}
/* If stack S is an empty stack, it returns TRUE; otherwise, it returns FALSE */
Status StackEmpty(LinkStack S)
{
if (S.count==0)
return TRUE;
else
return FALSE;
}
/* Returns the number of elements of S, that is, the length of the stack */
int StackLength(LinkStack S)
{
return S.count;
}
/* If the stack is not empty, use e to return the top element of S and return OK; Otherwise, ERROR is returned */
Status GetTop(LinkStack S,SElemType *e)
{
if (S.top==NULL)
return ERROR;
else
*e=S.top->data;
return OK;
}
/* Insert element e as the new stack top element */
Status Push(LinkStack *S,SElemType e)
{
LinkStackPtr s=(LinkStackPtr)malloc(sizeof(StackNode));
s->data=e;
s->next=S->top; /* Assign the current stack top element to the direct successor of the new node, as shown in figure ① */
S->top=s; /* Assign the new node s to the stack top pointer, as shown in figure ② */
S->count++;
return OK;
}
/* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
Status Pop(LinkStack *S,SElemType *e)
{
LinkStackPtr p;
if(StackEmpty(*S))
return ERROR;
*e=S->top->data;
p=S->top; /* Assign the stack top node to p, as shown in figure ③ */
S->top=S->top->next; /* Move the stack top pointer down one bit to point to the next node, as shown in figure ④ */
free(p); /* Release node p */
S->count--;
return OK;
}
Status StackTraverse(LinkStack S)
{
LinkStackPtr p;
p=S.top;
while(p)
{
visit(p->data);
p=p->next;
}
printf("\n");
return OK;
}
int main()
{
int j;
LinkStack s;
int e;
if(InitStack(&s)==OK)
for(j=1;j<=10;j++)
Push(&s,j);
printf("The elements in the stack are:");
StackTraverse(s);
Pop(&s,&e);
printf("Pop up stack top element e=%d\n",e);
printf("Stack empty No:%d(1:Null 0:no)\n",StackEmpty(s));
GetTop(s,&e);
printf("Stack top element e=%d Stack length is%d\n",e,StackLength(s));
ClearStack(&s);
printf("Empty stack after emptying stack No:%d(1:Null 0:no)\n",StackEmpty(s));
return 0;
}
Let's write about the chain storage structure of the stack implemented in Java. Because it is also a linear table, how to use the linear table implemented in Java can be viewed in my previous blog. Of course, Java generally uses the source code, or you can see the source code.
package text;
public class LinkStack {
private Node header = new Node(); // Create header node
class Node {
String value;
Node next;
}
public boolean push(String value) {
Node n = new Node();
n.value = value;
if(header.next == null) {
header.next = n;
return true;
}
n.next = header.next;
header.next = n;
return true;
}
public boolean pop() {
if(header.next == null) {
return false;
}
header.next = header.next.next;
return true;
}
public String getTop() {
if(header.next != null) {
return header.next.value;
}
return null;
}
public boolean isEmpty() {
return header.next == null ? true : false;
}
public static void main(String[] args) {
LinkStack stack = new LinkStack();
System.out.println(stack.isEmpty());
stack.push("aaa"); // Enter the stack
stack.push("bbb");
stack.push("ccc");
stack.push("ddd");
System.out.println(stack.isEmpty());
System.out.println(stack.getTop());
System.out.println(stack.pop());
System.out.println(stack.getTop());
}
}
The above java code does not realize genericity. You can also write it as genericity, which can be closer to the Java source code.
5, Comparison between sequential storage structure and chain storage structure
If the element changes during the use of the stack are unpredictable, sometimes small and sometimes very large, it is better to use the chain stack. On the contrary, if it changes within a controllable range, it is recommended to use the sequential stack.
6, Function of stack
When you first learn about stack, you may wonder why you should design such a restrictive data structure as stack. Isn't it good to use linear table directly? I also have such questions, but when you start from practical problems, you will find its usefulness. For example, when we return a web page to the previous web page, undo and other operations, the objects we operate are at the top of the stack, so we don't need to pay attention to other elements of the stack. Therefore, we don't need to make great efforts to use the linked list, Causing trouble is not conducive to the operation of the program.
7, Stack application I (recursion, Fibonacci sequence)
What is recursion? I believe everyone has learned this when learning C language, that is, the function itself calls itself. So what is the relationship between recursion and stack?
How recursion executes its forward and backward stages is not explained here. For detailed instructions, you can take a look at the special explanation. Here we focus on the relationship between stack and recursion. The backward order of a recursive process is the reverse of its forward order. Some operations may be performed during the return process, including restoring some data stored during the forward process. This method stores some data, and then restores the data in the reverse order of storage to provide the requirements for later use, which obviously conforms to the data structure of the stack. The forward process of recursion can be understood as pressing the stack, and the return process can be understood as processing the stack. The current high-level language does not need the writer to manage this stack, but is managed by the system. If you want to know, you can take a look at other materials.
Let's write the Fibonacci sequence
#include "stdio.h"
/* Fibonacci's recursive function */
int Fbi(int i)
{
if( i < 2 )
return i == 0 ? 0 : 1;
return Fbi(i - 1) + Fbi(i - 2); /* Here, Fbi is the function itself, which is equal to calling itself */
}
int main()
{
int i;
int a[40];
printf("The iteration shows the Fibonacci sequence:\n");
a[0]=0;
a[1]=1;
printf("%d ",a[0]);
printf("%d ",a[1]);
for(i = 2;i < 40;i++)
{
a[i] = a[i-1] + a[i-2];
printf("%d ",a[i]);
}
printf("\n");
printf("Recursively display Fibonacci sequence:\n");
for(i = 0;i < 40;i++)
printf("%d ", Fbi(i));
return 0;
}
8, Application of stack II (four arithmetic expressions)
When you see the four operations, do you wonder why these four operations should be implemented by stack instead of directly entering them? The four arithmetic expressions we want to understand here are the underlying principles of computer computing. How the computer calculates four complex operations. When we write the code now, the four operations have been written. We don't need to use the code to realize the four operations.
For the four operations, there is priority and order. In this order, the first operation will be carried out before the next operation. When we traverse a four operation expression, we will calculate the highest priority. For example, when we encounter the first bracket, we will enter the stack, when we encounter the last bracket, we will exit the stack, and put the results in the brackets for the next calculation, Isn't this process the concept of stack?
Of course, there are the concepts of suffix expression and infix expression, which will not be expanded... I don't know much.