Establish binary tree stored in binary linked list + traverse binary tree (first order, middle order, second order and sequence)
1. Establish a binary tree stored in a binary linked list
1-1. principle
The construction of binary tree uses the principle of recursion. When building a binary tree according to the pre order sequence, in order to let the computer know whether each node has left and right children, we should expand the original binary tree to clearly represent the left and right children of each node. If the current node has no left and right children, we use '#' to represent it.
The binary tree is extended from ordinary binary tree - > binary tree, as shown in the following figure:
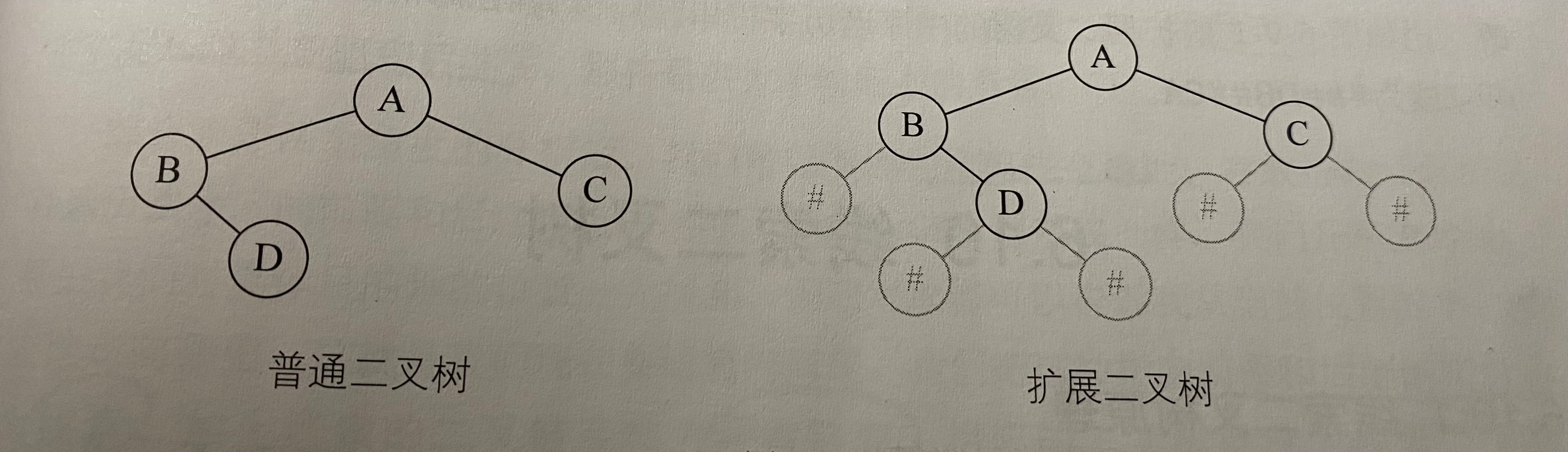
At this time, when we build the above binary tree according to the pre order sequence, the sequence we should enter is AB#D##C##
1-2. code
void CreateBiTree(BiTree *T) // Construction of binary tree
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
1-3. example
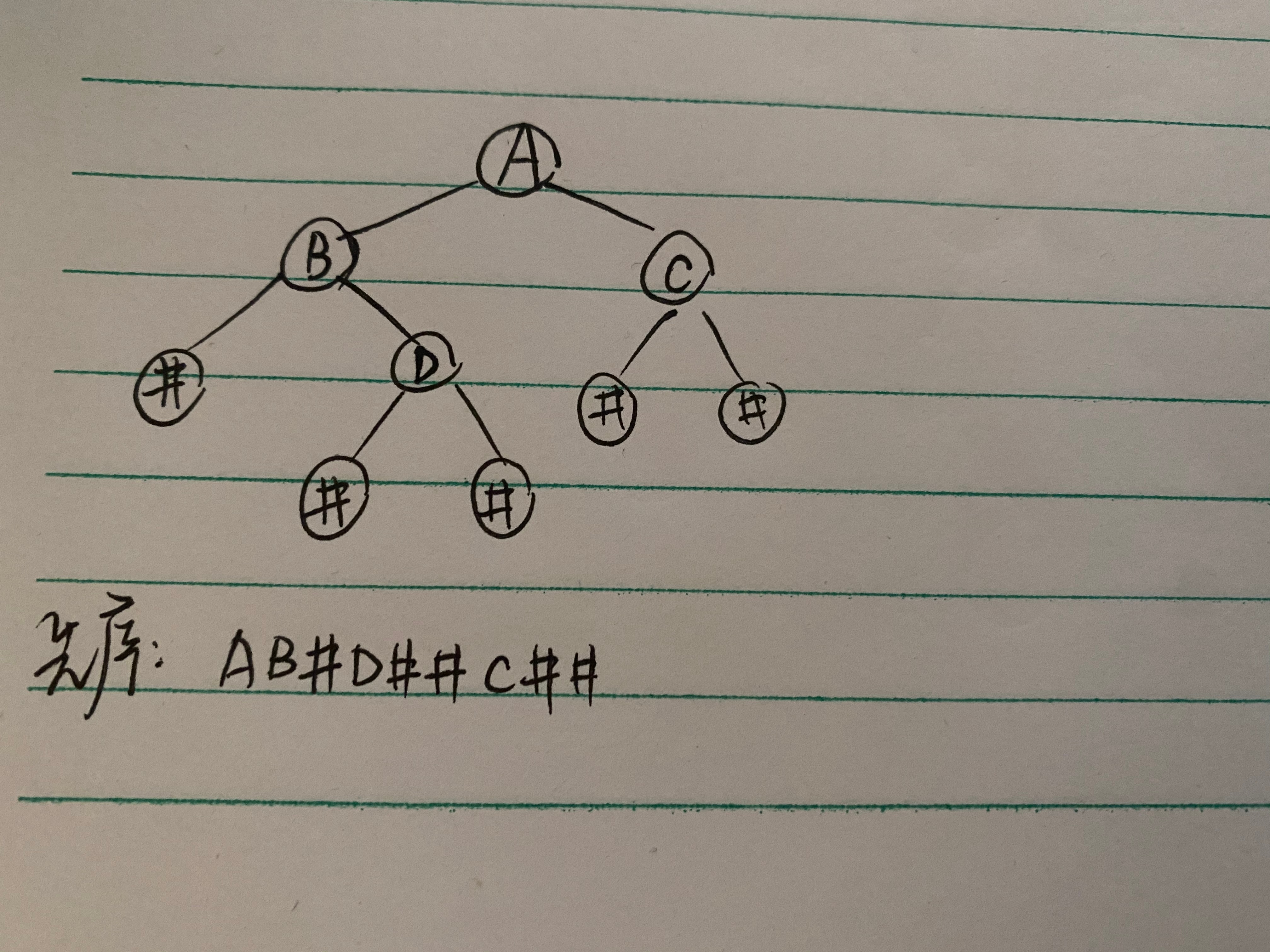
Take the binary tree in the following figure as an example: (the following examples take the binary tree as an example)
#include <iostream>
using namespace std;
const int N = 100;
typedef struct BiTNode
{
char data;
BiTNode *lchild;
BiTNode *rchild;
} BiTNode, *BiTree;
void CreateBiTree(BiTree *T) // Establish a binary tree stored in a binary linked list
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
printf("%c", (*T)->data); // Order of inspection establishment
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
int main()
{
BiTree T;
CreateBiTree(&T);
return 0;
}
2. Preorder traversal
2-1. recursion
If the binary tree is empty, return; Otherwise, the root node is accessed first, then the left subtree is traversed first, and finally the right subtree is traversed first.
void PreOrderTraverse(BiTree T) // Preorder traversal binary tree
{
if (T == NULL) return;
printf("%c", T->data); // Display node data first
PreOrderTraverse(T->lchild); // Then traverse the left subtree first
PreOrderTraverse(T->rchild); // Finally, the right subtree is traversed first
}
2-2. non-recursive
Stack:
(1) First, access the root node. The root node is stacked and enters its left subtree. Then, access the root node of the left subtree, stack and enter the left subtree of the next layer until the current node is empty.
(2) If the stack is not empty at this time, exit the top element of the stack and enter the right subtree of the node.
Repeat (1) and (2) until the current node and stack are empty.
void PreOrder(BiTree T) // Preorder traversal binary tree (non recursive)
{
BiTNode *s[N]; // Simulating stack with structure pointer array
int top = 0; // Set stack top pointer
BiTNode *p;
p = T;
while (top != 0 || p != NULL) { // If the current node is empty and the stack is empty, it ends
while (p != NULL) { // If the current node is not empty, access the root node, put the root pointer on the stack and enter the left subtree
printf("%c", p->data);
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // If the stack is not empty, the root pointer exits the stack and enters its right subtree
p = s[top--];
p = p->rchild;
}
}
}
2-3. example
Test input: ab#d##c##
Test output: abdc
#include <iostream>
using namespace std;
const int N = 100;
typedef struct BiTNode
{
char data;
BiTNode *lchild;
BiTNode *rchild;
} BiTNode, *BiTree;
void CreateBiTree(BiTree *T) // Establish a binary tree stored in a binary linked list
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
void PreOrderTraverse(BiTree T) // Preorder traversal of binary tree (recursion)
{
if (T == NULL) return;
printf("%c", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
void PreOrder(BiTree T) // Preorder traversal binary tree (non recursive)
{
BiTree s[N];
int top = 0;
BiTree p;
p = T;
while (p != NULL || top != 0) { // If the current node is not empty or the stack is not empty
while (p != NULL) { // Access the left subtree in turn and merge it into the stack
printf("%c", p->data);
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // Returns the top element of the stack and the root node of the current node, and enters the right subtree of the root node
p = s[top--];
p = p->rchild;
}
}
}
int main()
{
BiTree T;
CreateBiTree(&T);
PreOrderTraverse(T);
printf("\n");
PreOrder(T);
return 0;
}
3. Middle order traversal
3-1. recursion
If the binary tree is empty, return; Otherwise, first traverse the left subtree in middle order, then access the root node, and finally traverse the right subtree in middle order.
void InOrderTraverse(BiTree T)
{
if (T == NULL) return;
InOrderTraverse(T->lchild);
printf("%c", T->data);
InOrderTraverse(T->rchild);
}
3-2. non-recursive
Stack implementation:
(1) The root node is stacked into its left subtree, and then the root node of the left subtree is stacked into the left subtree of the next layer until the current node is empty.
(2) If the stack is not empty, exit the node of the previous layer from the top of the stack, access this node, and enter the right subtree of the node.
Repeat (1) and (2) until the current node and stack are empty.
void InOrder(BiTree T) // Middle order traversal binary tree (non recursive)
{
BiTNode *s[N]; // Simulating stack with structure pointer array
int top = 0; // Set stack top pointer
BiTNode *p;
p = T;
while (top != 0 || p != NULL) { // If the current node is empty and the stack is empty, it ends
while (p != NULL) { // If the current node is not empty, access the root node, put the root pointer on the stack and enter the left subtree
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // If the stack is not empty, the root pointer exits the stack and enters its right subtree
p = s[top--];
printf("%c", p->data); // After accessing the left node, return to the root node, and then access the root node
p = p->rchild;
}
}
}
3-3. example
Test input: ab#d##c##
Test output: bdac
#include <iostream>
using namespace std;
const int N = 100;
typedef struct BiTNode // Node structure of binary tree
{
char data; // Node data
BiTNode *lchild;
BiTNode *rchild; // Left and right child pointers
} BiTNode, *BiTree;
void CreateBiTree(BiTree *T) // Establish a binary tree stored in a binary linked list
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
void InOrderTraverse(BiTree T) // Middle order traversal binary tree (recursion)
{
if (T == NULL) return;
InOrderTraverse(T->lchild); // Traverse the left subtree in middle order first
printf("%c", T->data); // Display node data again
InOrderTraverse(T->rchild); // Finally, traverse the right subtree in middle order
}
void InOrder(BiTree T) // Middle order traversal binary tree (non recursive)
{
BiTNode *s[N]; // Simulating stack with structure pointer array
int top = 0; // Set stack top pointer
BiTNode *p;
p = T;
while (top != 0 || p != NULL) { // If the current node is empty and the stack is empty, it ends
while (p != NULL) { // If the current node is not empty, access the root node, put the root pointer on the stack and enter the left subtree
s[++top] = p;
p = p->lchild;
}
if (top != 0) { // If the stack is not empty, the root pointer exits the stack and enters its right subtree
p = s[top--];
printf("%c", p->data); // After accessing the left node, return to the root node, and then access the root node
p = p->rchild;
}
}
}
int main()
{
BiTree T;
CreateBiTree(&T);
InOrderTraverse(T);
printf("\n");
InOrder(T);
return 0;
}
4. Post order traversal
4-1. recursion
If the binary tree is empty, return; Otherwise, traverse the left subtree in sequence, then access the root node, and finally traverse the right subtree in sequence.
void PostOrderTraverse(BiTree T)
{
if (T == NULL) return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c", T->data);
}
4-2. non-recursive
It is also implemented by stack:
(1) The root node is stacked into its left subtree, and then the root node of the left subtree is stacked into the next left subtree until the current node is empty.
(2) If the stack is not empty, if the right subtree of the top node P of the stack is empty or has been accessed, exit the stack, access the P node, assign p to q, and set p to empty; If the top node of the stack has a right subtree and is not accessed, it enters the right subtree of P.
Repeat (1) and (2) until the current node and stack are empty.
void PostOrder(BiTree T) // Post order traversal binary tree (non recursive)
{
BiTNode *s[N];
int top = 0;
BiTNode *p, *q; // q stores the node just accessed, and p stores the current root node
p = T;
q = NULL;
while (p != NULL || top != 0) {
while (p != NULL) {
s[++top] = p;
p = p->lchild;
}
if (top != 0) {
p = s[top]; // Get stack top element
if (p->rchild == NULL || p->rchild == q) { // If the right subtree is empty or the right subtree has just been accessed
top--; // Stack top element out of stack
printf("%c", p->data);
q = p;
p = NULL;
}
else {
p = p->rchild;
}
}
}
}
4-3. example
Test input: ab#d##c##
Test output: dbca
#include <iostream>
using namespace std;
const int N = 100;
typedef struct BiTNode // Node structure of binary tree
{
char data; // Node data
BiTNode *lchild, *rchild; // Left and right child pointers
} BiTNode, *BiTree;
void CreateBiTree(BiTree *T) // Establish a binary tree stored in a binary linked list
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
void PostOrderTraverse(BiTree T) // Post order traversal binary tree (recursion)
{
if (T == NULL) return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c", T->data);
}
void PostOrder(BiTree T) // Post order traversal binary tree (non recursive)
{
BiTNode *s[N];
int top = 0;
BiTNode *p, *q; // q stores the node just accessed, and p stores the current root node
p = T;
q = NULL;
while (p != NULL || top != 0) {
while (p != NULL) {
s[++top] = p;
p = p->lchild;
}
if (top != 0) {
p = s[top]; // Get stack top element
if (p->rchild == NULL || p->rchild == q) { // If the right subtree is empty or the right subtree has just been accessed
top--; // Stack top element out of stack
printf("%c", p->data);
q = p;
p = NULL;
}
else {
p = p->rchild;
}
}
}
}
int main()
{
BiTree T;
CreateBiTree(&T);
PostOrderTraverse(T);
printf("\n");
PostOrder(T);
return 0;
}
5. Sequence traversal
5-1. Sequence traversal code
Sequence traversal is realized by queue. First, the root node enters the queue. When the queue is not empty, repeat the following two operations:
(1) The queue head node is out of the queue and accesses the out of queue node.
(2) Non empty left and right children at the out of line node join the team.
void LevelOrder(BiTree T) // Sequence traversal of binary tree
{
BiTNode *Q[N]; // Array emulation queue
int front = 0;
int rear = 0;
BiTNode *p;
Q[++rear] = T; // Root node join
while (front != rear) { // If the queue is not empty
// The queue head node is out of the queue and accesses the out of the queue node
p = Q[++front];
printf("%c", p->data);
// The non empty left and right children at the out of line node join the team in turn
if (p->lchild != NULL) {
Q[++rear] = p->lchild;
}
if (p->rchild != NULL) {
Q[++rear] = p->rchild;
}
}
}
5-2. example
Test input: ab#d##c##
Test output: abcd
#include <iostream>
using namespace std;
const int N = 100;
typedef struct BiTNode
{
char data;
BiTNode *lchild;
BiTNode *rchild;
} BiTNode, *BiTree;
void CreateBiTree(BiTree *T) // Establish a binary tree stored in a binary linked list
{
char ch;
scanf("%c", &ch);
if (ch == '#') *T = NULL; // #Indicates that the current node is empty
else {
*T = (BiTree)malloc(sizeof(BiTNode)); // Dynamic application node memory
(*T)->data = ch; // Generate root node
CreateBiTree(&(*T)->lchild); // Construct left subtree
CreateBiTree(&(*T)->rchild); // Construct right subtree
}
}
void LevelOrder(BiTree T) // Sequence traversal of binary tree
{
BiTNode *Q[N]; // Array emulation queue
int front = 0;
int rear = 0;
BiTNode *p;
Q[++rear] = T; // Root node join
while (front != rear) { // If the queue is not empty
// The queue head node is out of the queue and accesses the out of the queue node
p = Q[++front];
printf("%c", p->data);
// The non empty left and right children at the out of line node join the team in turn
if (p->lchild != NULL) {
Q[++rear] = p->lchild;
}
if (p->rchild != NULL) {
Q[++rear] = p->rchild;
}
}
}
int main()
{
BiTree T;
CreateBiTree(&T);
LevelOrder(T);
return 0;
}
Content reference:
Dahua data structure, Cheng Jie
Data structure and algorithm Wang Shuyan