Hello, I'm a fisherman from Go school. Today, let's talk about the implementation of workflow based on directed acyclic graph

01 workflow overview

Workflow is a model that organizes and executes the work in the workflow according to certain rules. For example, overtime application and leave application in common administrative systems; The problem to be solved by workflow is to realize a specific goal and let multiple participants automatically transfer information according to a certain reservation rule.

This paper introduces a workflow based on directed acyclic graph. Through directed acyclic graph, two problems can be solved: logically, the dependencies of each node are organized; Technically, nodes with dependencies need to wait for execution, and nodes without dependencies can execute concurrently.

The practical application of the workflow is the process from receiving request to advertising response in programmed advertising: the dependent execution between various nodes, such as receiving request, obtaining geographical location, obtaining user portrait, advertising recall, advertising sorting, algorithm prediction, returning response and so on.

However, the goal of this article is to introduce its implementation idea, so the example section will take the process of dressing as an example.

02 implementation of Workflow

Let's take the event of getting up and dressing in the morning as an example to explain the implementation of directed acyclic graph. The events included in the dressing process include wearing underwear, pants, socks, shoes, watches, shirts, coats, etc. Some of these events must wear certain clothes before wearing other clothes (such as socks before shoes). Some events can be worn in any order (for example, socks and trousers can be worn in any word order). As shown in the figure:

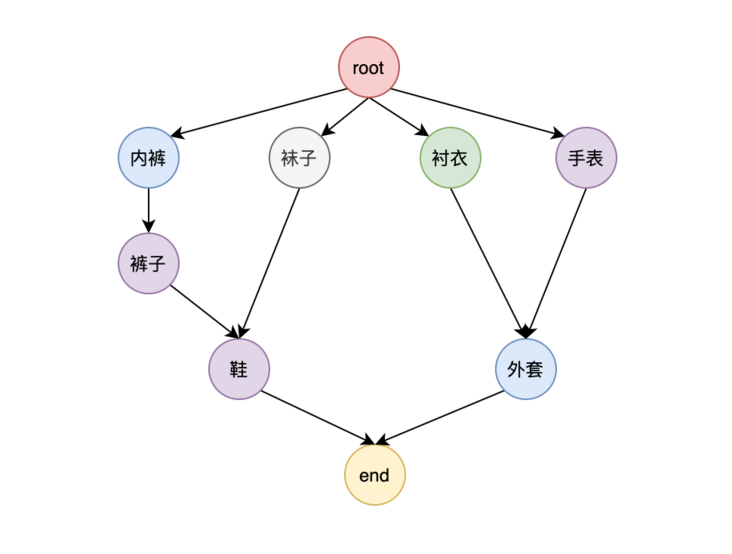
As can be seen from the above figure, there is no interdependence between wearing underwear, socks, shirts and watches, which can be executed concurrently. Shoes can only be worn after the pants and socks on which they depend are worn. Let's take a look at how to implement such a directed acyclic graph workflow.

2.1 define workflow structure

According to the above figure, we can see that a relatively complete workflow includes start nodes (where to start), edges (which nodes to pass through) and end nodes (where to end). Therefore, we define the structure of workflow as follows:

type WorkFlow struct {
    done chan struct{} //End ID, which is written by the end node
  doneOnce *sync.Once //Ensure that it is written only once during concurrency
  alreadyDone bool //Terminate process flag when there is a node error
    root *Node //Start node
    End *Node //End node
    edges []*Edge //All passing edges, edges connect nodes
}

2.2 define edges in Workflow

Edges are used to represent dependencies between two nodes. The edge in a directed graph can also indicate which of the two nodes is the front node and which is the rear node. The post node cannot execute until the task of the pre node is completed. As shown in the figure below:

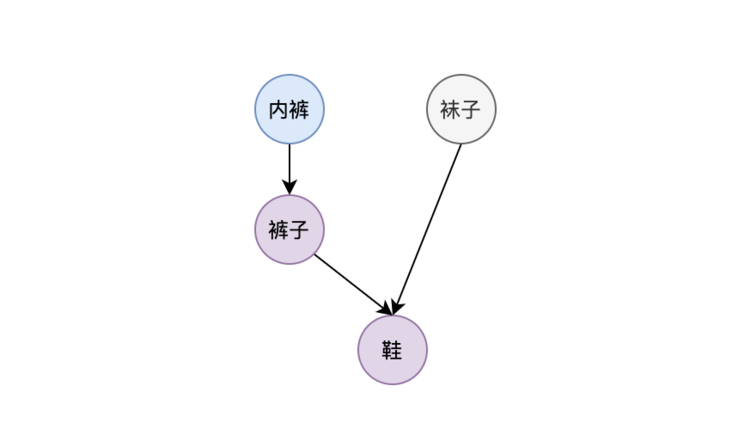
The underwear and pants nodes indicate that pants can only be worn after wearing underwear, so the underwear wearing node is the front node of the pants wearing node; Shoes can only be worn after pants and socks are worn, so pants and socks are the front node of shoes.

So the representation of the edge is from which node to which node. It is defined as follows:

type Edge struct {
    FromNode *Node
    ToNode *Node
}

2.3 defining nodes in Workflow

A node is a task unit that specifically executes logic. At the same time, each node has an associated edge. Because we use a directed graph, the associated edges are divided into an in edge (that is, the edge ending at the vertex) and an out edge (that is, the edge starting from the vertex). As shown below:

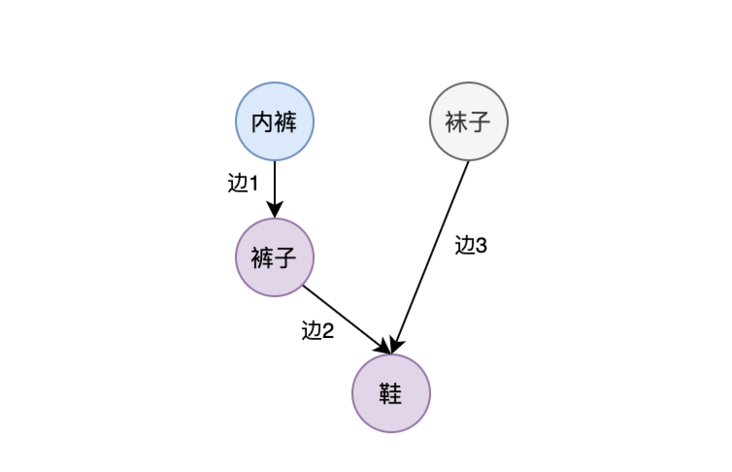
Edge 1 is not only the out edge of the underwear node, but also the in edge of the pants node. Edge 2 and edge 3 are the entry edges of the shoe node. In this paper, the incoming edge is called the dependent edge of the node, which is defined as Dependency, which means that the node can start to execute only after the tasks of the nodes connected by these edges are executed. The outgoing edge of the node is called the child edge, and Children is defined to represent the child nodes that can continue to execute after the node is executed. Therefore, the structure of the node is defined as follows:

type Node struct {
    Dependency []*Edge //Dependent edge
    DepCompleted int32 //Indicates how many dependent edges have been executed. It is used to judge whether the node can execute
    Task Runnable //Task execution
    Children []*Edge //Word edge of node
}

In the node definition, we see that there is a Runnable type. This type is an interface with only one Run(i interface {}) method, which is used to abstract the business logic of the node. So that when the node executes, it can call the Run method of each node uniformly. The interface is defined as follows:

type Runnable interface {    
    Run(i interface{})
}

We take the shoe wearing task as an example to implement the interface, which is defined as follows:

type WearShoesAction struct {}

func (a *WearShoesAction) Run(i interface{}) {
    fmt.Println("I'm putting on my shoes...")
}

With a specific execution task, we can build the task on a node:

func NewNode(Task Runnable) *Node {
    return &Node{
        Task: Task,
    }
}

//Building nodes with shoes
shoesNode := NewNode(&WearShoesAction{})

With nodes, we need to build edges. Because edges connect two nodes, we define a sock wearing node:

type WearSocksAction struct {
    
}

func(a *WearSocksAction) Run(i interface{}) {
    fmt.Println("I'm wearing socks...")
}

Well, with two nodes, we define the function of the edge to build the two nodes into edges:

func AddEdge(from *Node, to *Node) *Edge {
    edg := &Edge{
        FromNode: from,
        ToNode: to,
    }
    
    //This edge is the outgoing edge of the from node
    from.Children = append(from.Children, edge)
    //This edge is the incoming edge of the to node
    to.Dependency = append(to.Dependency, edge)
    
    return edg
}

2.4 special nodes in workflow -- start node and end node

In addition, we see a start node and an end node in the workflow. The start node is the root node of the workflow and the trigger point for the execution of the whole workflow. Its Task is to trigger child nodes. There is no specific business logic to execute in all nodes, that is, the Task in this node is nil.

The end node represents that the tasks of the whole workflow have been completed, and signals the caller that the process is over. Therefore, the task logic of this node is to write a message to the done channel of the workflow and let the caller receive the message to unblock:

type EndWorkFlowAction struct {
  done chan struct{} //After the node completes execution, write a message to the done and share it with the done in the workflow
  s *sync.Once //Concurrency control to ensure that you write to done only once
}


//End the specific execution task of the node
func (end *EndWorkFlowAction) Run(i interface{}) {
    end.s.Do(func() { end.Done <- struct{} })
}

2.5 build workflow

Well, let's look at the structure definition based on the above elements and how to build a complete workflow and make the workflow work.

First, of course, instantiate a workflow.

func NewWorkFlow() *WorkFlow {
    wf := &WorkFlow{
        root: &Node{Task: nil},//The start node. All specific nodes are its child nodes. There is no specific execution logic, only for the execution of other nodes
        done: make(chan struct{}, 1),
        doneOnce: &sync.Once{},
    }
    
    //Join end node
    EndNode = &EndWorkFlow{
        done: wf.done,
        s: wf.doneOnce,
    }
    wf.End = NewTaskNode
    
    return wf
}

Because each workflow instance must have a start node and an end node, we specify the start node and end node during initialization.

Secondly, the edges between nodes are constructed. There are three types of construction edges. One is the edge formed between the heel node and the intermediate node. The characteristic of this type is that the root node has only out edges and no in edges. One is the edge between intermediate nodes and intermediate nodes. The last kind is the edge between the middle node and the end node. The characteristic of this kind of edge is that the end node has only in edge and no out edge.

func (wf *WorkFlow) AddStartNode(node *Node) {
    wf.edges = append(wf.edges, AddEdge(wf.root, node))
}

func (wf *WorkFlow) AddEdge(from *Node, to *Node) {
    wf.edges = append(wf.edges, AddEdge(from, to))
}

func (wf *WokFlow) ConnectToEnd(node *Node) {
    wf.edges = append(wf.edges, AddEdge(node, wf.End))
}

Through the above three functions, we can construct the relationship diagram between each node in the workflow. With the diagram, we need to make
The diagram flows. So let's look at the definition of related execution behavior in workflow.

func (wf *WorkFlow) StartWithContext(ctx context.Context, i interface{}) {
    wf.root.ExecuteWithContext(ctx, wf, i)
}

func(wf *WorkFlow) WaitDone() {
    <-wf.done
    close(wf.done)
}

func(wf *WorkFlow)  interrupDone() {
    wf.alreadyDone = true
    wf.s.Do(func() { wf.done <- struct{} })
}

2.6 implementation logic of nodes

In the workflow execution function, we see that the ExecuteWithContext function of the root node is called. Let's look at the specific implementation of this function.

func (n *Node) ExecuteWithContext(ctx context.Context, wf *WorkFlow, i interface{}) {
    //If the dependent front node has not finished running, it will be returned directly
    if !n.dependencyHasDone() {
        return
    }
    //There is a node running error. The execution of the process is terminated
    if ctx.Err() != nil {
        wf.interruptDone()
        return
    }
    
    //Node specific operation logic
    if n.Task != nil {
        n.Task.Run(i)
    }
    
    //Run child node
    if len(n.Children) > 0 {
        for idex := 1; idx < len(n.Children); idx++ {
            go func(child *Edge) {
                child.Next.Execute(ctx, wf, i)
            }(n.Children[idx])
        }
        
        n.Children[0].Next.Execute(ctx, wf, i)
    }
    
}

Most of the logic is simple. Let's focus on the dependencyHasDone() function. This function is used to check whether all the edges on which a node depends have been executed. This is achieved by counting. The specific implementation is as follows:

func (n *Node) dependencyHasDone() bool {
    //This node does not have a dependent front node and does not need to wait. It directly returns true
    if n.Dependency == nil {
        return true
    }
    
    //If the node has only one dependent front node, it also returns directly
    if len(n.Dependency) == 1 {
        return true
    }
    
    //Here, add 1 to the dependent node to indicate that a dependent node has been completed
    atomic.AddInt32(&n.DepCompleted, 1)
    
    //Judge whether the current number of dependent nodes is equal to the number of dependent nodes, which indicates that they are all running
    return n.DepCompleted == int32(len(n.Dependency))
}

Let's take the following figure as an example to illustrate how the end node is checked and the dependent front nodes are executed.

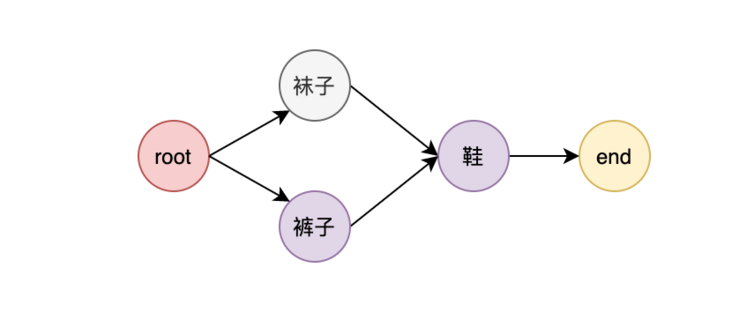
First, the root node starts to execute its own ExecuteWithContext method. In this method, the dependencyHasDone function is used to judge whether all the preceding nodes that the node depends on have been executed, but the node has no preceding node, that is, n.Dependency == nil is satisfied and true is returned, so the root node can continue to execute the following logic in ExecuteWithContext.

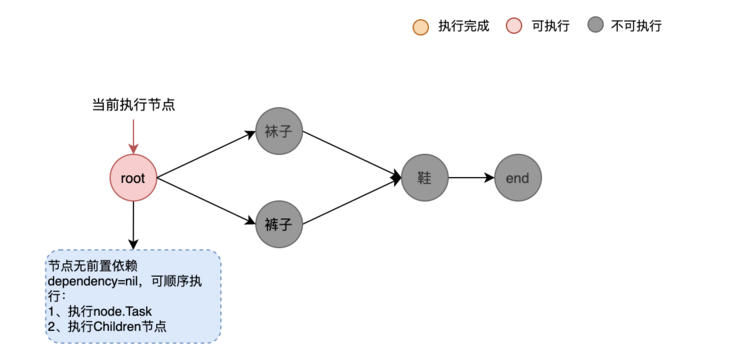
Execute the Task of root. Because the Task of root is nil, continue to execute to the child node. It is found that there are two edges in the Children of root, and the loop starts to let the child nodes execute at the same time. That is, the pants node and socks node are executed.

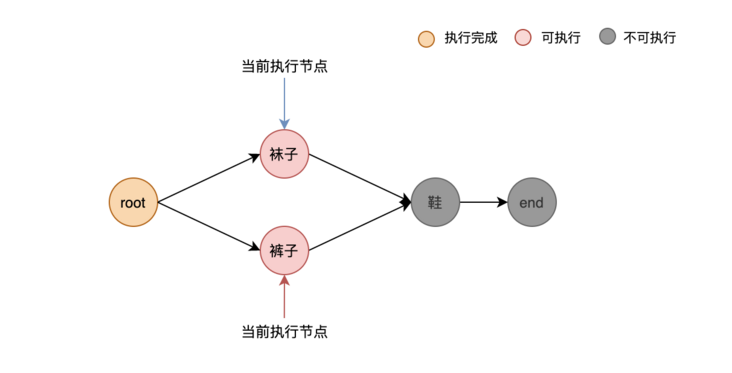
We know that the sock node and pants node depend on only root, that is, there is only one entry edge. When it is executed by itself, it indicates that the root node has finished executing, so the following logic is executed:

    //If the node has only one dependent front node, it also returns directly
    if len(n.Dependency) == 1 {
        return true
    }

Suppose that the pants node is executed first, but the socks node is not executed yet. After the pants node is executed, it will find its own child node to continue to execute, that is, the shoe node. At this time, when the shoe node executes the dependency hasdone logic, it hits the logic in the third part:

//Here, add 1 to the dependent node to indicate that a dependent node has been completed
    atomic.AddInt32(&n.DepCompleted, 1)
    
//Judge whether the current number of dependent nodes is equal to the number of dependent nodes, which indicates that they are all running
return n.DepCompleted == int32(len(n.Dependency))

It is found that there are 2 edges on which the shoes depend. Now only one item has been completed, so it is in an unenforceable state, so it will be returned directly and will no longer be executed. As shown in the figure below:

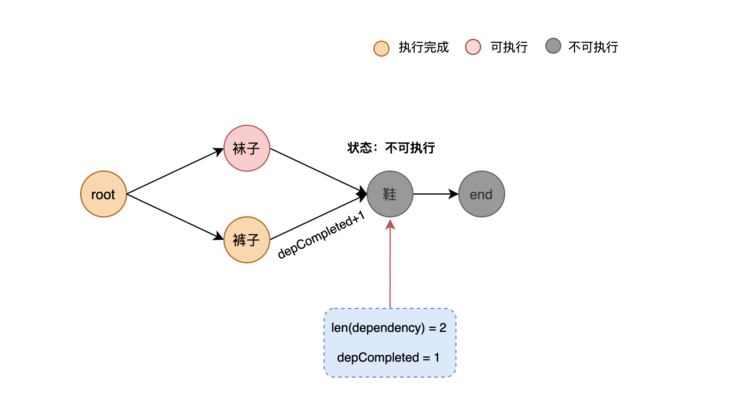
At this time, the sock node execution is over. It will also execute its own child node, that is, the shoe node. At this time, it is found that the completion number of the shoe node is 2, and it is found that it is equal to its dependent edge. At this time, the shoe node is programmed in an executable state. As shown below:

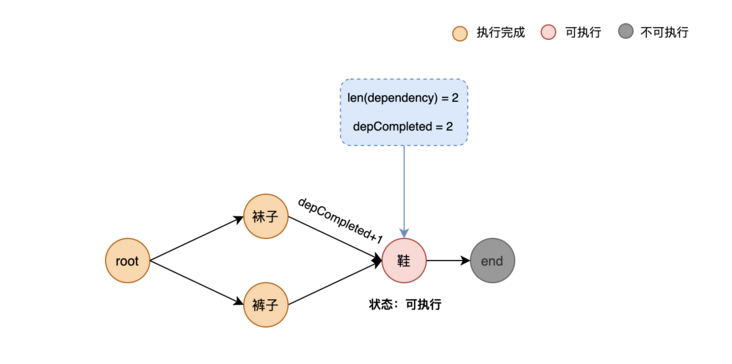
2.7 complete example

Let's now look at a complete example of the dressing process.

wf := NewWorkFlow()

//Build node
UnderpantsNode := NewNode(&WearUnderpantsAction{})
SocksNode := NewNode(&WearSocksAction{})
ShirtNode := NewNode(&ShirtNodeAction{})
WatchNode := NewNode(&WatchNodeAction{})
TrousersNode := NewNode(&WearTrouserNodeAction{})
ShoesNode := NewNode(&WearShoesNodeAction{})
CoatNode := NewNode(&WearCoatNodeAction{})

//Building relationships between nodes
wf.AddStartNode(UnserpatnsNode)
wf.AddStartNode(SocksNode)
wf.AddStartNode(ShirtNode)
wf.AddStartNode(WatchNode)

wf.AddEdge(UnserpatnsNode, TrousersNode)
wf.AddEdge(TrousersNode, ShoesNode)
wf.AddEdge(SocksNode, ShoesNode)
wf.AddEdge(ShirtNode, CoatNode)
wf.AddEdge(WatchNode, CoatNode)

wf.ConnectToEnd(ShoesNode)
wf.ConnectToEnd(CoatNode)

var completedAction []string

wf.StartWithContext(ctx, completedAction)
wf.WaitDone()

fmt.Println("Perform other logic")

The structure of each Action in the above code can implement the Runnable interface, which will not be repeated here. At this point, we have successfully built the dressing flow chart we saw at the beginning.

03 some other questions

3.1 how to transfer data between nodes

We can see that the second parameter in the StartWithContext function of WorkFlow is an interface {} type, which is used to pass parameters to each Node. At the same time, the parameters in the ExecuteWithContext function of Node are also of interface {} type. We can define this parameter as a pointer type. In this way, the content pointed to by the pointer can be changed during the execution of each Node.

3.2 how to terminate the process if there is a node execution error

In a process, if there is an error in the execution of any node, our processing method is to terminate the whole process. That is, the ExecuteWithContext function of the above node has the judgment of the following code:

    if ctx.Err() != nil {
        wf.interruptDone()
        return
    }

Let's take a look at the implementation of interruptDone in WorkFlow:

wf.alreadyDone = true
wf.s.Do(func() { wf.done <- struct{}{}})

summary

Directed acyclic graph is a powerful tool to solve node dependencies. It not only solves the problem of dependencies, but also solves the concurrency problem of independent nodes.