| There are five commonly used shortest path algorithms in graph theory. They are coming. All the villains are coming 💣 The enemy has five seconds to reach the battlefield~ |

💓 On graph theory
| Graph theory has a long history, but graph theory is an important concern in both company interview and programming competition. Now there may be many partners preparing for the Blue Bridge Cup. Here is the test point on graph theory pasted by the author from the official website of the Blue Bridge Cup. |

| Graph theory is also a regular guest in the interview |

| For this article, the author summarizes and shares the shortest path problem in the test site, and other graph theory problems continue to emerge in the follow-up~ |
🌟 Knowledge foreshadowing
🌻 Definition of graph
A graph is generally defined and described by a binary g = (V, e) or g = < V, E >. Where V is the set of vertices of graph G and E is the set of edges in graph G.
|
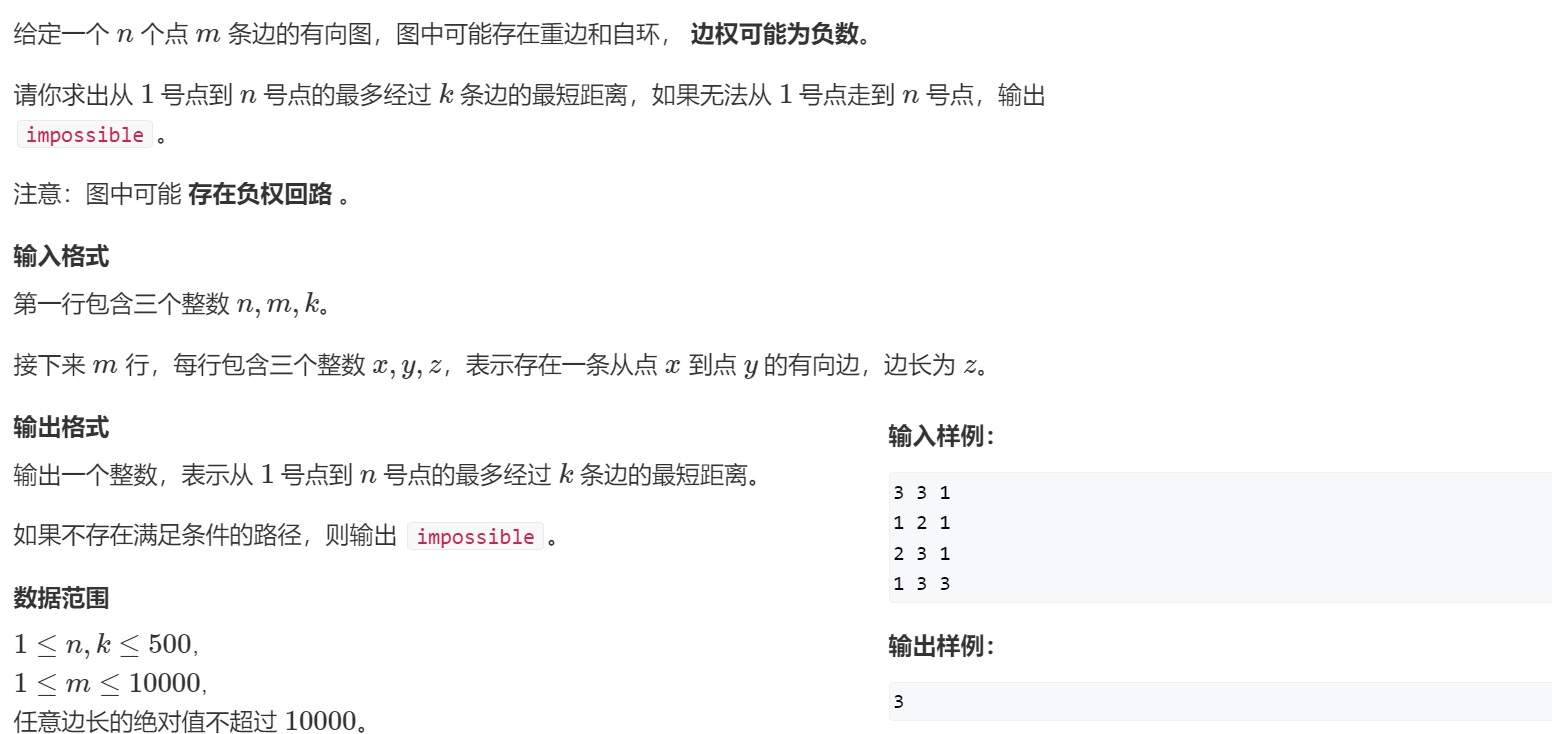
🌻 adjacency matrix
| To put it more simply, it is to map the information given in the title to a two-dimensional matrix. |
| In combination with the above figure, point 0 can go to point 1. In the two-dimensional matrix on the right, point 1 and point 0 on the position mark corresponding to (0,1) cannot go to point 2. Let (0,2) still be point 0, point 0 can go to point 3, let (0,3) mark 1, and so on |
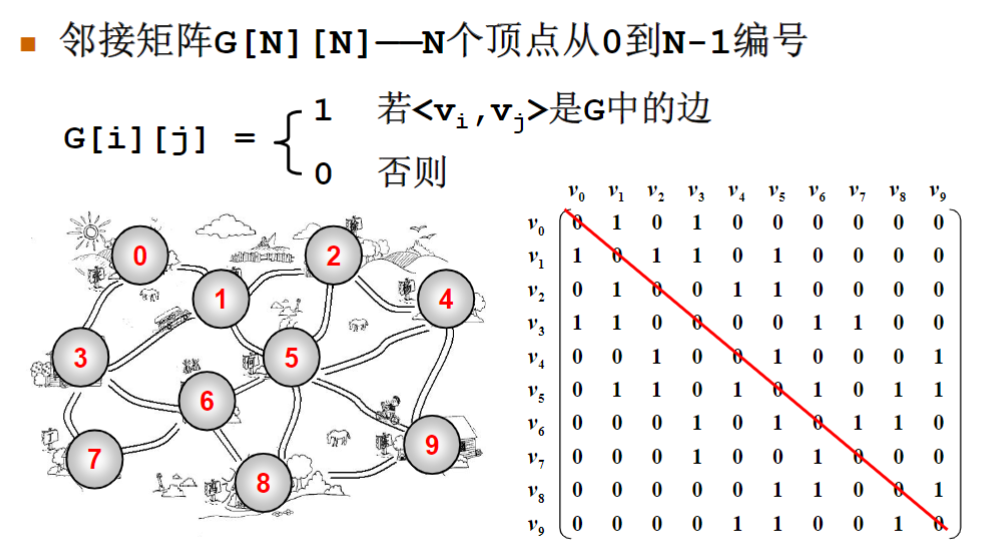
🌻 Adjacency table
| To be simple and rough is to string some connected points into a linked list according to the information given by the topic |
| Still use the village example just now. Point 4 can go to points 2, 5 and 9, and then string them on a linked list. Write the whole 0 ~ 9 points side by side |
💓 General outline of shortest path algorithm
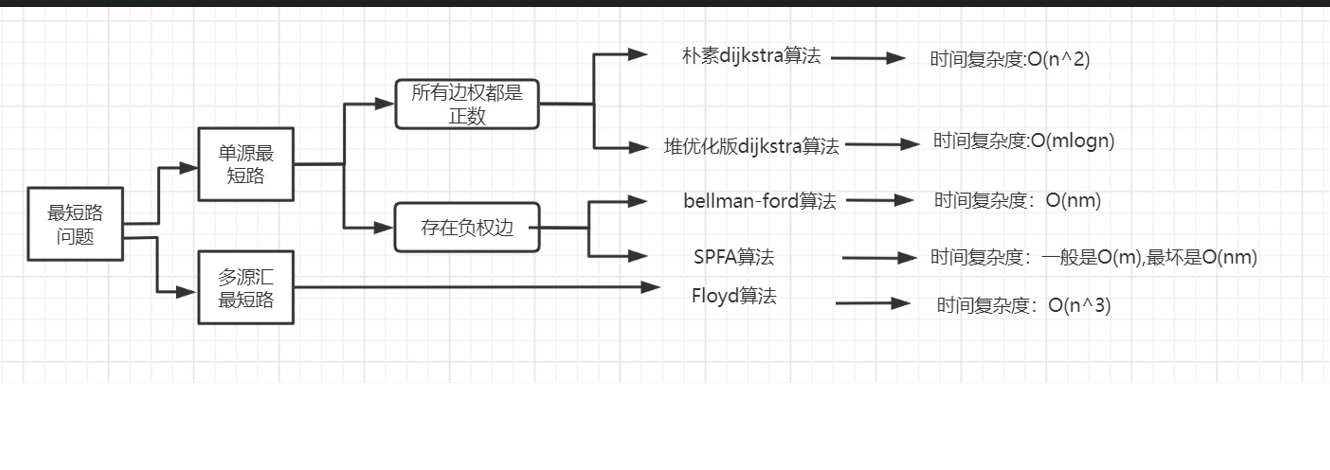
| Friends, in this picture, you should keep in mind how to use the corresponding types of shortest path algorithms under different backgrounds and the time complexity of each shortest path algorithm 😉 |
💓 dijkstra algorithm
🌟 Naive dijsktra algorithm (applicable to dense graphs)
🌻 Example description
| It is stated in the title that there is no negative weight edge. According to the data range given in the title, there are few points and many edges. Therefore, it can be found that it is a dense graph, so it can be solved directly with the simple version of dijkstra. |
🌻 Reference code (C + + version)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 510;
int n,m; //Points and edges in a graph
int g[N][N]; //adjacency matrix
int dist[N]; //Represents the distance from point 1 to each point in the figure
bool st[N]; //Store the identified shortest point
//Complete the function called
void dijkstra()
{
memset(dist,0x3f,sizeof dist); //To process the distance array dist, first set all points to positive infinity
dist[1] = 0; //Handle point 1, indicating that the distance from point 1 to point 1 is 0
//n-1 cycles
for(int i = 0; i < n-1;i++)
{
int t = -1;
//Process each point
for(int j = 1; j <= n;j++)
//If the current j is not in the st record status array
//T = = - 1 | dist [t] > dist [j] means that this t was previously assigned by other j, and now a better one appears, or the value of this t has not been modified directly
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true; //Put this point into the set
//Use t to update the distance from other points to point 1
for(int j = 1; j <= n;j++)
dist[j] = min(dist[j],dist[t]+g[t][j]);
}
}
int main()
{
//Enter points and edges
scanf("%d%d",&n,&m);
//Initialize adjacency matrix
memset(g,0x3f,sizeof g);
//m times of inquiry and the process of drawing construction
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
//Save to the drawing, just deal with the heavy edges
g[a][b] = min(g[a][b],c);
}
//Call dijkstra
dijkstra();
//Output results
if(dist[n] == 0x3f3f3f3f) printf("%d",-1);
else printf("%d\n",dist[n]);
return 0;
}
🌻 Algorithm template
The specific operation flow of the simple dijkstra algorithm can be described in the following figure:
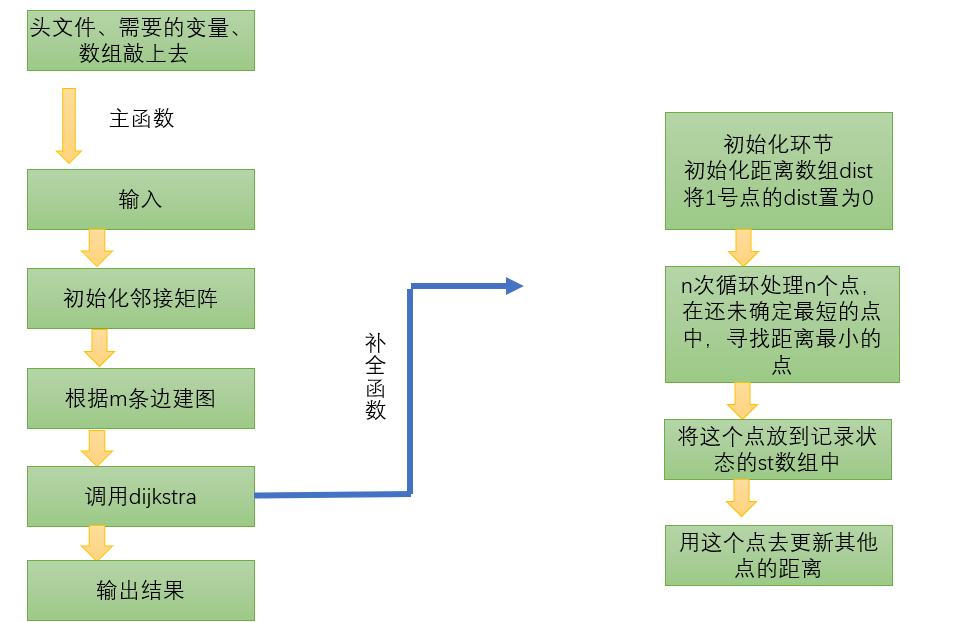
The specific code template of the simple dijkstra algorithm is as follows:
int g[N][N]; // Store each edge
int dist[N]; // Store the shortest distance from point 1 to each point
bool st[N]; // Store whether the shortest circuit of each point has been determined
void dijkstra()
{
//Initialization link
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // Find the point with the smallest distance among the points where the shortest path has not been determined
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
// Update the distance of other points with the global minimum variable t
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
🌻 Detail implementation
1, Heavy edge
| When building a graph, we need to focus on dealing with multiple edges, and finally only leave the shortest edge to build the graph |
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
/use min The function filters out the shortest edge to build the graph
g[a][b] = min(g[a][b],c);
}
2, The idea of initialization
| Use the memset function to initialize the given address in bytes. Because it is to find the minimum path, initialize the distance from point 1 to each point as a large data, and finalize the distance from point 1 to point 1 as 0 |
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
3, Find the point with the smallest distance among the points where the shortest path has not been determined
| The core of the whole code is "! st[j]", and all operations are carried out at the point j currently ready to explore without being determined. |
| For: int t = -1; It means that a variable t is declared to record the minimum value for the whole world. At the beginning, it is assigned a non-existent - 1. Using this minimum value to update all its outgoing edges is also carried out according to the idea of finding the global minimum value, so the shortest path can be obtained at last |
Finally, after all n points have been tried, put the global minimum variable t into the array st in which the shortest path state has been determined, "st[t] = true"
for (int i = 0; i < n - 1; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
😉 Happy Ac

🌟 Heap optimized dijkstra algorithm (applicable to sparse graph)
It can be seen from the above program code that its time complexity is O(n2). The main bottleneck affecting efficiency is to find the global minimum variable. Here, it enumerates next to next, and the efficiency will be relatively poor

Therefore, a heap can be used to maintain the dist array. The minimum value can be obtained in O(logn) time and deleted from the heap. Then an edge can be expanded and updated in O(logn) time. Finally, O(mlogn) can be used to realize the heap optimized version of dijkstra algorithm.
🌻 Example description
🌻 Reference implementation code (C + + version)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int,int> PII; //Use a pair number to maintain the distance and node number
int n,m;
const int N = 1e6+10;
int h[N],e[N],ne[N],w[N],idx; //Sparse graph, saved with adjacency table
int dist[N];
bool st[N];
void add(int a,int b ,int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
void dijkstra()
{
//Initialization link
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
//Create a small root heap using the STL container
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({0,1}); //The first attribute of the number pair is the distance, and the second attribute is the node
//Operate when the heap is not empty
while(heap.size())
{
//Take out the point with the smallest current distance each time. For the small root heap, that is, the top of the heap
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if(st[ver]) continue; //If this node is already in st, it means that redundant backup is being explored. Just skip it
st[ver] =true; //Mark this node to determine the shortest path
//Update other points with the current point
for(int i = h[ver]; i != -1; i = ne[i])
{
//Get the node stored in the adjacency table and store the node data in j
int j = e[i];
//Start update
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j],j}); //Insert the updated data into the heap
}
}
}
}
int main()
{
//input
scanf("%d%d",&n,&m);
//Initialize adjacency table
memset(h,-1,sizeof h);
//Construction drawing according to m edges
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
//Call dijkstra function
dijkstra();
//output
if(dist[n] == 0x3f3f3f3f) puts("-1");
else printf("%d",dist[n]);
return 0;
}
🌻 Algorithm template
The operation flow of dijkstra algorithm of heap optimization version can be shown in the following figure:
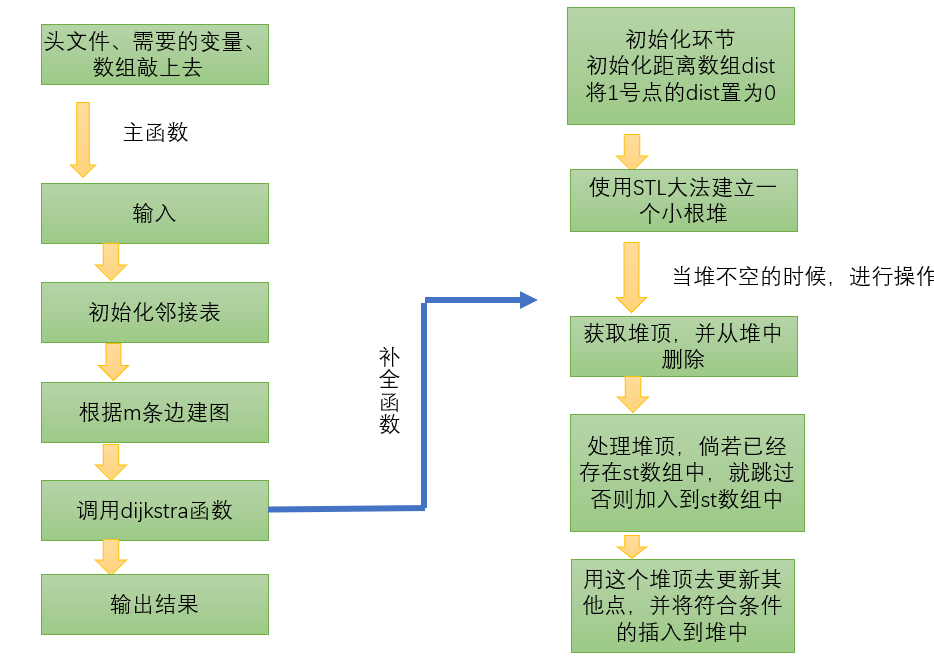
The code of heap optimized dijkstra algorithm is described as follows:
typedef pair<int, int> PII;
int n,m; // Number of points
int h[N], w[N], e[N], ne[N], idx; // The adjacency table stores all edges
int dist[N]; // Store the distance from all points to point 1
bool st[N]; // Is the shortest distance to store each point determined
void dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first storage distance, second storage node number
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
}
🌻 Detail implementation
1, Establishment of adjacency table
| The idea is as like as two peas, but only one weight should be recorded. If you are not familiar with the static list, you can look at this buddy. |
Data structure - good helper for competition, static linked list
2, It is recommended to memorize the line of code for creating a small root heap
3, Data acquisition
| After obtaining the heap top, continue to obtain the corresponding distance, node number and other data through the first and second attributes |
Chic Ac

💓 Bellman Ford algorithm
Look back at the algorithm outline 😉
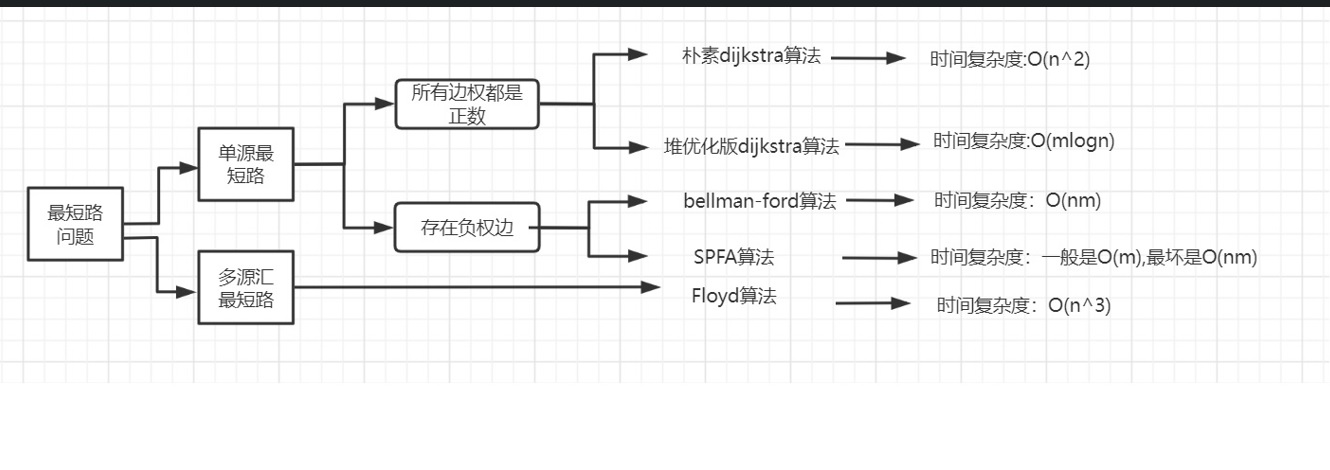
| Bellman Ford algorithm and SPFA algorithm are used in the context of single source and negative weight edge. On the whole, SPFA is better than Bellman Ford algorithm, but for the shortest path problem with limited number of edges, Bellman Ford algorithm can only be used |
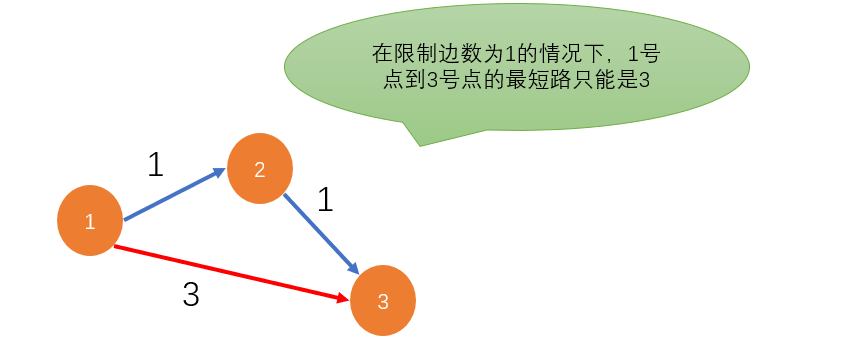
🌻 Example description - shortest path with edge number limit
🌻 Reference code (C + + version)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 510 , M = 10010;
int n,m,k;
int dist[N];
int backup[N];
//Structure of storage point and weight
struct Edge{
int a,b,w;
}edges[M];
void bellman_ford()
{
//Initialization link
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
//Iterative k-edges
for(int i = 0 ; i < k ; i++)
{
//backups
memcpy(backup,dist,sizeof dist);
//Deal with the shortest circuit on each side
for(int j = 0; j < m;j++)
{
//Get information for each point
int a = edges[j].a,b = edges[j].b,w = edges[j].w;
//Find shortest path
dist[b] = min(dist[b],backup[a]+w);
}
}
}
int main()
{
//input
scanf("%d%d%d",&n,&m,&k);
//Mapping
for(int i = 0; i < m ;i++)
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i] = {a,b,w};
}
//Call function
bellman_ford();
//Output results
if(dist[n] > 0x3f3f3f3f / 2) puts("impossible");
else printf("%d\n",dist[n]);
return 0;
}
🌻 Algorithm template
The flow chart of Bellman Ford algorithm implementation is as follows:
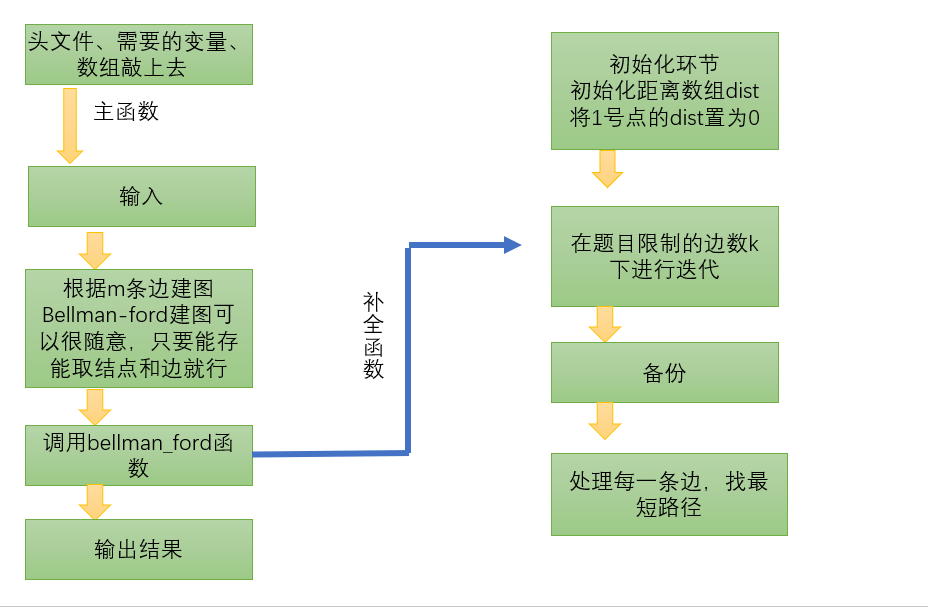
The bellman Ford algorithm code is described as follows:
int n, m; // n represents the number of points and m represents the number of sides
int dist[N]; // dist[x] stores the shortest distance from 1 to X
struct Edge // Edge, a represents the point, b represents the entry point, and w represents the weight of the edge
{
int a, b, w;
}edges[M];
void bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// If the n-th iteration still relaxes the trigonometric inequality, it indicates that there is a shortest path with a length of n+1. According to the drawer principle, there are at least two identical points in the path, indicating that there is a negative weight loop in the graph.
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
}
🌻 Detail implementation
1, Backup - in order to ensure that the condition of edge number limit can not be broken
memcpy(backup,dist,sizeof dist);
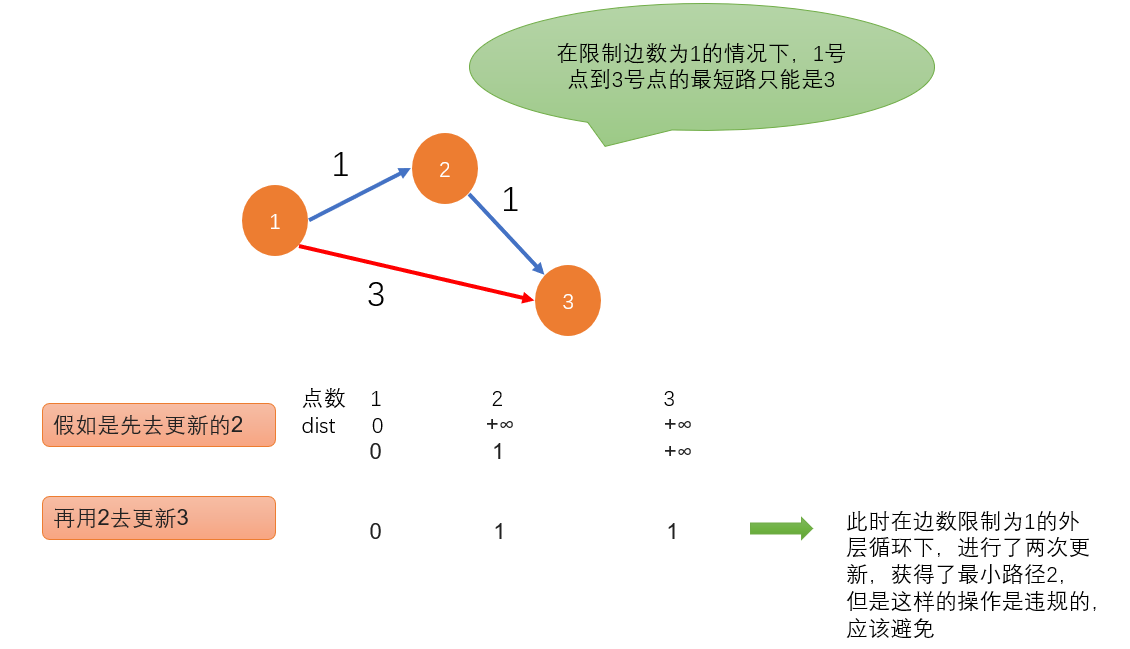
| In order to avoid this, although the operation is indeed carried out under the number of sides k of the outer loop, a similar situation occurs when the inner loop goes to explore the point, so a backup operation is taken to curb this situation |
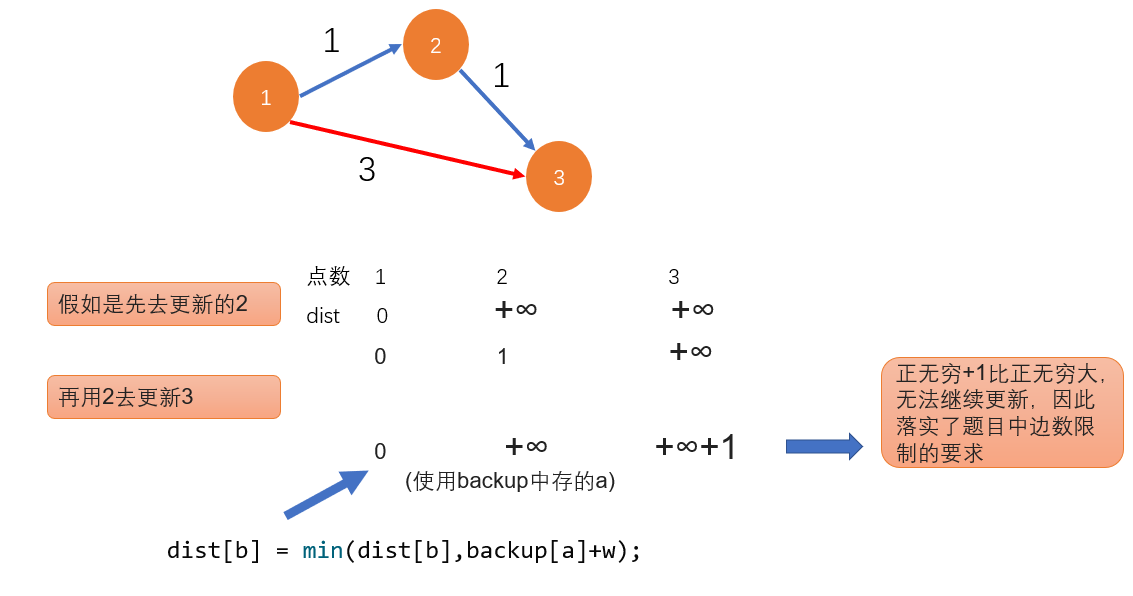
2, Happy Ac

💓 SPFA algorithm
spfa is usually called "Bellman Ford algorithm for queue optimization" internationally
🌻 Example description

🌻 Reference code (C + + version)
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa()
{
//Initialization link
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
//Create a queue and queue point 1 that has confirmed the shortest path
queue<int> q;
q.push(1);
//Mark points that have been queued
st[1] = true;
//Perform a series of operations when the queue is not empty
while (q.size())
{
//Get the team leader and get the team leader out of the team
int t = q.front();
q.pop();
//Mark points that are not in the queue
st[t] = false;
//Use the team head to explore its exit
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
//If the conditions are met, update the distance from point 1 to j
dist[j] = dist[t] + w[i];
//If this point is not in the queue
if (!st[j])
{
//Join the team, mark
q.push(j);
st[j] = true;
}
}
}
}
}
int main()
{
//input
scanf("%d%d", &n, &m);
//Initialize adjacency table
memset(h, -1, sizeof h);
//Mapping
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
//Call function
spfa();
//output
if (dist[n] == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", dist[n]);
return 0;
}
🌻 Algorithm template
The flow chart of SPFA algorithm implementation is as follows:
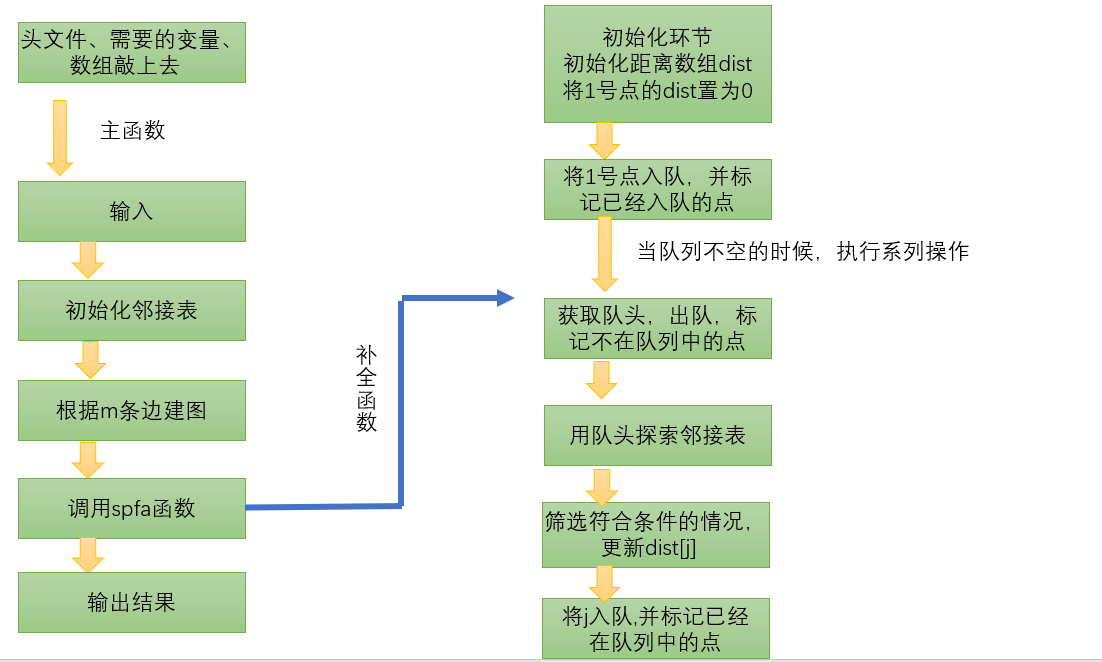
The code of SPFA algorithm is described as follows:
int n; // Total points
int h[N], w[N], e[N], ne[N], idx; // The adjacency table stores all edges
int dist[N]; // Store the shortest distance from each point to point 1
bool st[N]; // Stores whether each point is in the queue
void spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // If j already exists in the queue, there is no need to insert j repeatedly
{
q.push(j);
st[j] = true;
}
}
}
}
}
🌻 Detail implementation
1, Team entry and marking
| After updating the new point j with t, remember to judge whether this point has been marked. If not, add it to the queue and put it into the st array for marking |
2, Associative memory
| The essence of SPFA is to optimize the bellman Ford algorithm with queues, but the implementation is very similar to the heap optimized version of dijkstra algorithm, the queue for SPFA and the priority queue for dijkstra |
Happy Ac

💓 Floyd algorithm
In order to find the shortest path between any two points in the graph, that is Shortest path outline The shortest path problem of multiple sources and sinks in. For the shortest path problem between any two points, the graph is generally dense and the implementation is very simple.
The idea of Floyd algorithm:
Split the multi-source shortest path into N times of single source shortest path.
In Dijkstra algorithm, the single source shortest path uses two cycles. The time complexity is O (N2). Floyd sets a layer of cycle n in the outermost layer, so the time complexity is O(n3)
🌻 Example description

🌻 Reference code (C + + version)
#include <cstring>
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 210,INF = 1e9;
int n,m, Q;
int d[N][N];
void floyd()
{
for(int k = 1; k <= n;k++)
for(int i = 1; i <= n;i++)
for(int j = 1;j <= n;j++)
d[i][j] = min(d[i][j],d[i][k]+d[k][j]);
}
int main()
{
scanf("%d%d%d",&n,&m,&Q);
//Initialize adjacency matrix
for(int i = 1;i <= n;i++)
for(int j = 1; j <= n;j++)
if(i == j) d[i][j] = 0;
else d[i][j] = INF;
//Create diagram
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
d[a][b] = min(d[a][b],c);
}
//Call function
floyd();
//Handle Q queries
while(Q--)
{
int a,b;
scanf("%d%d",&a,&b);
if(d[a][b] > INF / 2) puts("impossible");
else printf("%d\n",d[a][b]);
}
return 0;
}
🌻 Algorithm template
Flow chart of Floyd algorithm implementation:
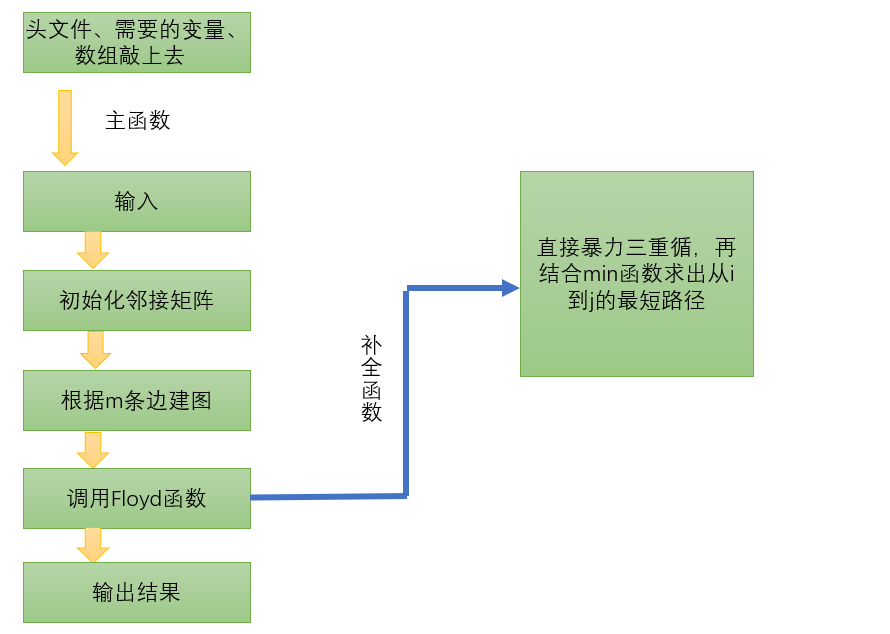
Floyd algorithm code Description:
initialization:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// After the algorithm, d[a][b] represents the shortest distance from a to B
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
🌻 Detail implementation
1, Initialization
if (i == j) d[i][j] = 0; else d[i][j] = INF;
| d array represents the distance from i to j, so during initialization, i == j should be initialized to 0, and other positions should be initialized to an infinite number |
2, Output
| Because the edge weight can be negative, d[a][b] is not necessarily INF, so the judgment condition is changed to d[a][b] is still a relatively large number |
if(d[a][b] > INF / 2) puts("impossible");
else printf("%d\n",d[a][b]);
Thank you for your patience ~, if you are biased, please point it out in a private letter in time 💖💖💖
Continuous updat ing of basic algorithm~