A. Ancient Civilization

Title portal

I'll give you an array a (decimal) with a length of n,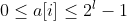, now ask you to take out an ANS (decimal system),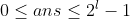, so that the sum of position differences corresponding to a[i] (binary) and ans (binary) is minimized.

Take chestnuts for example: the binary of a[i]=5 is 101, and the binary of ans=10 is 1010. When we look from right to left, we find that the first, second, third and fourth bits are different. The current difference degree is 4, and the sum of difference degrees is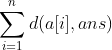

Idea: the difficulty of this problem is to understand the problem (hey, you should be able to understand the problem). In fact, this is a choice problem. The maximum number of ANs (binary) bits is l bits. We only need to consider whether to take or not to take the current i-th bit. In order to minimize the difference, we store the number of 1 of the i-th bit of all numbers (binary) in the pre array, and then, If the number of {1 of the current i-th bit is greater than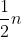Just take it (half the time, just take it or not, I don't take it here)

Core code:

if(pre[i]>n-pre[i])b[i]=1;//b [] array is used to store the binary of ans

Fast power:

int kuai(int s,int n){
	int ans=1;
	while(n){
		if(n&1)ans*=s;
		s*=s;
		n>>=1;
	}
	return ans;
}

Quick read:

inline int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    } while('0' <= ch && ch <= '9') {
        x = x * 10 + ch - '0';
        ch = getchar();
    } return x * f;
}

To achieve all this, we also have to have a decimal conversion binary (bloggers can only rub it by hand in 2022), and the final fast power (of course, pow can be used, but pow is of double type, and you can't think of it when there is a problem) to find the ans answer. After so much, go to the code

t=read();//t group of data, here bloggers use fast reading to reduce time
while(t--){
	n=read();l=read();//n numbers, l is the maximum number of binary digits
	for(i=1;i<=n;i++)a[i]=read();
	for(i=1;i<=n;i++){
		da1=a[i];sum=1;        //
		while(da1){            //Hand rubbing decimal to binary
			if(da1%2){         //
				pre[sum]++;    //
			}                  //
			da1>>=1;           //
			sum++;             //
		}
	}
	for(i=1;i<=l;i++)if(pre[i]>n-pre[i])b[i]=1;//Calculate ans (binary)
	ans=0;//Don't forget to update ans Oh, t group data
	for(i=1;i<=l;i++)if(b[i])ans+=kuai(2,i-1);//Hand rub binary to decimal, kuai(2,i-1) is a fast power, and bloggers won't release it here
	cout<<ans<<endl;
	for(i=1;i<=l;i++)pre[i]=0;//Don't forget to update the status of the new pre array
}
return 0;

B. Elementary Particles

Title portal

Meaning: t group of data, give you an array a with a length of n. now you are required to intercept two subsequences with different but equal lengths in the array. The only requirement is to make at least one corresponding position the same as the numbers above, and find out the maximum length (if it does not exist, output - 1)

 

For example, 1 2 3 and 5 2 7 satisfy the condition, because their second positions are equal, while 1 3 2 and 2 1 3 do not satisfy the condition

Idea: since this is an existential problem, we must directly consider that as long as there is an equal existence, now we give you an a array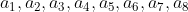At this time, if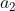and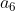Equal, then what is the maximum number of sequences composed of them at this time? yes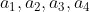and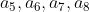. We found that as long as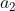The length of the left sequence, and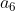The length of the sequence on the right. Why? because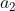stay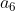On the left, so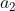How long can you get on the left,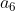We can get it, so let's see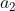On the left, similarly, this is what we only look at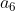Reason on the right

Key steps: therefore, we only need to use sort to sort the structure (use the structure question to save the position of each number when saving it)

Key formula: we now make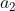The position of is l, so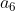If the position of is r, then the length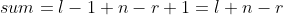, because n is a known quantity, we only need to consider the minimum l - r, and because our structures are sorted, we just need to calculate the one with the smallest absolute value of the difference between the two adjacent values (provided that the values of the two numbers are equal), and finally add it to n

Key codes:

cmp:

bool cmp(node x,node y)
{
	if(x.da==y.da)return x.xu<y.xu;//In fact, this step is redundant, but I wrote it for peace of mind, because cmp will not continue to be arranged 
	return x.da<y.da;
}

By the way, when writing, just use the idea of taking a ruler and move l and r together

Upper Code:

struct node{
	int xu,da;//xu is the position and da is the value 
}a[500005];
bool cmp(node x,node y)
{
	if(x.da==y.da)return x.xu<y.xu;//In fact, this step is redundant, but I wrote it for peace of mind, because cmp will not continue to be arranged 
	return x.da<y.da;
}
signed main()
{
	int i,j,t;int n,l,r,sum;//n numbers, t groups of data, l, r the position of the sequence after the current sequencing, and sum is the value 
//	jian1;jian2;jian3;//l. Interpretation of the position of r, for example, now 1, 8, 3, now l is 2, then the position in the current sequence is 2
	t=read();//Read quickly 
	while(t--){
		n=read();
		for(i=1;i<=n;i++){
			a[i].da=read();
			a[i].xu=i;//The location of the current number 
		}
		sort(a+1,a+1+n,cmp);//sort 
		sum=-1;l=1;r=2;//l must be less than r. of course, you want him to change the back
		while(r<=n){//r can't be out of bounds (⊙ o ⊙), there are n numbers in total 
			if(a[l].da==a[r].da)sum=max(sum,a[l].xu+n-a[r].xu);//After all, the final answer is the best value, so it has to be compared 
			l++;r++;//L the number of current positions has been used and has no value, so l++ 
		}
		cout<<sum<<endl;//Output answer 
	}
	return 0;
}

C. Road Optimization

Title portal

Meaning: for a road with a length of len, n give the speed limit sign (the first speed limit sign must be above the starting point), use the coordinates represented by array a with a length of n (unit: km), and then give an array b corresponding to array a to record the time required per kilometer from the ith sign to the i+1 sign. The algorithm is as follows: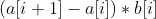, now you are allowed to delete up to k points (or not (⊙), please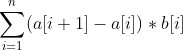minimum

Idea: take a look at this question, um Found no ideas, look at the second eye, um No idea, put it

In fact, this question should be used dynamic programming , local optimization makes global optimization (provided that there is no aftereffect, that is, no matter what you choose in the front, it will not affect the latter choice). Therefore, I write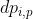It means to keep the ith speed limit sign (i.e. not delete), and then there are still p places to delete (i.e. P speed limit signs can also be deleted). Now the key is how to write the dp equation

Key codes:

dp equation: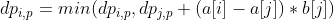

Here, i'll give the dp equation first. What's the j in it? The j in it is the speed limit sign q from the j to the i. all are deleted (excluding i, J). For us, the final destination is also a point, that is, a[n+1]=len

Here you may ask, because it is connected to delete, won't it leak? Of course not. Now solve your doubts:

Firstly, we reserved the ith one, which makes us solve the problem of aftereffect. No matter how the previous one is deleted, even if it breaks the day, it will not affect the subsequent deletion. Secondly, j is less than i, which means that all the speed limit signs q from the jth to the ith are deleted (excluding i, J), so we are the best step by step

No more nonsense, just go to the code:

signed main()
{
	int i,j,t;int n,len,p,k;
	n=read();
	len=read();
	k=read();
	for(i=1;i<=n;i++)a[i]=read();
	for(i=1;i<=n;i++)b[i]=read();
	a[++n]=len;
	for(i=1;i<=n;i++)for(j=0;j<=k;j++)dp[i][j]=1e15;//We have to initialize the dp array first. After all, we compare the minimum value step by step, so we initialize it to the maximum value 
	dp[1][k]=0;
	for(i=2;i<=n;i++)
		for(j=1;j<i;j++)
			for(p=0;p<=k;p++)//To use dp equation, we must first ensure that there are no more than k road signs deleted, and there are i-j-1 between I and J 
				if(p+i-j-1<=k)dp[i][p]=min(dp[i][p],dp[j][p+i-j-1]+(a[i]-a[j])*b[j]);
	cout<<*min_element(&dp[n][0],&dp[n][k+1])<<endl;//Because the answer is updated step by step, we only need to find the minimum value of 0-k deleted at n 
	return 0;
}

Because the blogger was too delicious, he didn't write it out at that time. He made up questions after the game++

I hope you have made progress after reading this article. Come on! (⊙0⊙)!

By the way, push a problem solution that knows the boss above Codeforces Round #765 (Div. 2) A~D - Zhihu (zhihu.com)

The blogger's dp was learned from this big man. The main reason is that the big man spoke a little abstruse. The blogger has understood it for a long time