Original link: http://tecdat.cn/?p=20424
introduce
Time series provides a method for predicting future data. Based on previous values, time series can be used to predict economic and weather trends. The specific properties of time series data mean that special statistical methods are usually required.
In this tutorial, we will first introduce and discuss the concepts of autocorrelation, stationarity and seasonality, and then continue to apply one of the most commonly used time series prediction methods, called ARIMA.
A method available in Python for modeling and predicting future points of time series is called SARIMAX, which represents seasonal autoregressive comprehensive moving average with seasonal regression. Here, we will focus on ARIMA, which is used to fit time series data to better understand and predict future points in time series.
In order to take full advantage of this tutorial, it may be helpful to be familiar with time series and statistics.
In this tutorial, we will use Jupyter Notebook to process data.
Step 1 - install the package
To set up our time series prediction environment:
cd environments . my_env/bin/activate
From here on, create a new directory for our project.
mkdir ARIMA cd ARIMA
Now let's install stats models and the data mapping package matplotlib.
pip install pandas numpy statsmodels matplotlib
Step 2 - Import package and load data
To start using our data, we'll start Jupiter Notebook:
To create a new notebook file, select new > Python 3 from the drop-down menu at the top right:
First import the required libraries:
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')We will use the CO2 data set, which collects CO2 samples from March 1958 to December 2001. We can introduce these data as follows:
y = data.data
Let's preprocess the data. Weekly data processing is more troublesome, because the time is relatively short, so let's use the monthly average. We can also use the fillna() function to ensure that there are no missing values in the time series.
# The "MS" string groups data into storage at the beginning of the month
y = y['co2'].resample('MS').mean()
# Fill in missing values
y = y.fillna(y.bfill())Output co2 1958-03-01 316.100000 1958-04-01 317.200000 1958-05-01 317.433333 ... 2001-11-01 369.375000 2001-12-01 371.020000
Let's explore this time series with data visualization:
plt.show()

When we plot the data, we can find that the time series has an obvious seasonal pattern, and the overall trend is upward.
Now, we continue to use ARIMA for time series prediction.Step 3 - ARIMA time series model
The most common method used in time series prediction is called ARIMA model. Arima is a model that can fit time series data in order to better understand or predict the future points in the series.
Three different integers (p, d, q) are used to parameterize the ARIMA model. Therefore, ARIMA model symbolizes ARIMA(p, d, q). These three parameters together describe the seasonality, trend and noise in the data set:
- p is the of the model_ Autoregressive_ part. It enables us to incorporate the impact of past values into the model. Intuitively, this is similar to saying that if the weather has been warm for the past three days, it may be warm tomorrow.
- d is the difference part of the model. Contains the difference component to be applied to the time series (that is, the number of past time points to subtract from the current value). Intuitively, this is similar to that if the temperature difference in the last three days is very small, the temperature tomorrow may be the same.
- q is the of the model_ Moving average_ part. This allows us to set the error of the model as a linear combination of error values observed in the past at previous time points.
When dealing with seasonal effects, we use_ Seasonality_ ARIMA (expressed as ARIMA(p,d,q)(P,D,Q)s. Here, (P, D, q) is a non seasonal parameter. Although (P, D, q) follows the same definition, it is applicable to the seasonal component of time series. The term s is the periodicity of the time series (4 quarters, 12 years).
In the next section, we will describe how to automatically identify the best parameters for the seasonal ARIMA time series model.
Step 4 - parameter selection of ARIMA time series model
When we want to use seasonal ARIMA model to fit time series data, our primary goal is to find the value of ARIMA(p,d,q)(P,D,Q)s to optimize the target index. There are many guidelines and best practices to achieve this goal, but the correct parameterization of ARIMA model can be a difficult manual process, requiring domain expertise and time. Other statistical programming languages, such as R, provide automated methods to solve this problem, but these methods have not been ported to python. In this section, we will solve this problem by writing Python code to programmatically select the best parameter values of ARIMA(p,d,q)(P,D,Q)s time series model.
We will use grid search to iteratively explore different combinations of parameters. For each parameter combination, we use SARIMAX() in the module to fit the new seasonal ARIMA model. After exploring the entire parameter range, our optimal parameter set will become a set of parameters that produce the best performance. Let's first generate the various parameter combinations we want to evaluate:
#Define the p, d, and q parameters to take any value between 0 and 2 p = d = q = range(0, 2) # Generate all different combinations of p, q, and q triples pdq = list(itertools.product(p, d, q)) # Generate all different seasonal p, q and q combinations seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
Output Examples of parameter combinations for Seasonal ARIMA... SARIMAX: (0, 0, 1) x (0, 0, 1, 12) SARIMAX: (0, 0, 1) x (0, 1, 0, 12) SARIMAX: (0, 1, 0) x (0, 1, 1, 12) SARIMAX: (0, 1, 0) x (1, 0, 0, 12)
Now, we can use the triplet parameters defined above to automate the process of training and evaluating ARIMA models on different combinations. In statistics and machine learning, this process is called grid search (or hyperparametric optimization) for model selection.
When evaluating and comparing statistical models with different parameters, each model can be ranked according to its degree of fitting data or its ability to accurately predict future data points. We will use the AIC (Akaike Information Criterion) value, which can easily return statsmodes by using the fitted ARIMA model. AIC measures the degree to which the model fits the data while considering the overall complexity of the model. A model that uses a large number of features will obtain a larger AIC score than a model that uses fewer features to achieve the same goodness of fit. Therefore, we look for a model that produces the lowest AIC.
The following code block iterates through parameter combinations and uses the SARIMAX function statsmodels in to fit the corresponding Season ARIMA model. After fitting each SARIMAX() model, the code will output their respective AIC scores.
warnings.filterwarnings("ignore") # Specifies that warning messages are ignored
try:
mod = sm.tsa.statespace.SARIMAX(y,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)The above code produces the following results
Output SARIMAX(0, 0, 0)x(0, 0, 1, 12) - AIC:6787.3436240402125 SARIMAX(0, 0, 0)x(0, 1, 1, 12) - AIC:1596.711172764114 SARIMAX(0, 0, 0)x(1, 0, 0, 12) - AIC:1058.9388921320026 SARIMAX(0, 0, 0)x(1, 0, 1, 12) - AIC:1056.2878315690562 SARIMAX(0, 0, 0)x(1, 1, 0, 12) - AIC:1361.6578978064144 SARIMAX(0, 0, 0)x(1, 1, 1, 12) - AIC:1044.7647912940095 ... ... ... SARIMAX(1, 1, 1)x(1, 0, 0, 12) - AIC:576.8647112294245 SARIMAX(1, 1, 1)x(1, 0, 1, 12) - AIC:327.9049123596742 SARIMAX(1, 1, 1)x(1, 1, 0, 12) - AIC:444.12436865161305 SARIMAX(1, 1, 1)x(1, 1, 1, 12) - AIC:277.7801413828764
The output of the code shows that the lowest value of the AIC value of SARIMAX(1, 1, 1)x(1, 1, 1, 12) is 277.78. Therefore, of all the models we consider, we should consider it as the best choice.
Step 5 - fitting ARIMA time series model
Using grid search, we identified a set of parameters that produced the best fit model for our time series data. We can continue to analyze this model in more depth.
We will start by inserting the best parameter values into the new SARIMAX model:
results = mod.fit()
Output
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.3182 0.092 3.443 0.001 0.137 0.499
ma.L1 -0.6255 0.077 -8.165 0.000 -0.776 -0.475
ar.S.L12 0.0010 0.001 1.732 0.083 -0.000 0.002
ma.S.L12 -0.8769 0.026 -33.811 0.000 -0.928 -0.826
sigma2 0.0972 0.004 22.634 0.000 0.089 0.106
==============================================================================The attribute SARIMAX produced by the summary output returns a lot of information, but we focus on the coefficients. The coef column shows the weight (i.e., importance) of each function and how each function affects the time series. P> Column|z| tells us the importance of each feature weight. Here, the p value of each weight is less than or close to 0.05, so it is reasonable to keep all weights in our model.
When fitting the seasonal ARIMA model, it is important to run the model diagnostic program to ensure that the assumptions made by the model are not violated.
plt.show()
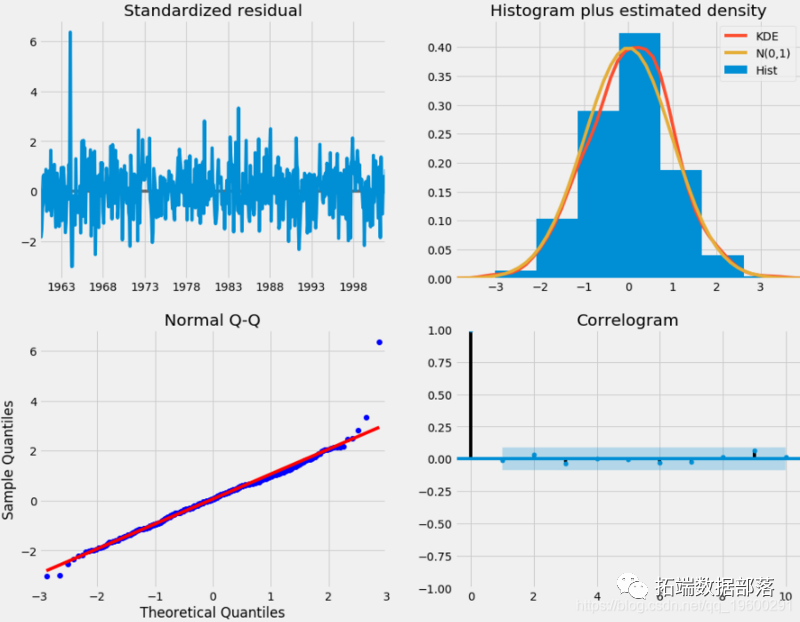
Our main concern is to ensure that the residuals of the model are uncorrelated and zero mean normal distribution. If the seasonal ARIMA model does not meet these attributes, it indicates that it can be further improved.
In this case, our model diagnosis suggests normal distribution of model residuals according to the following:
- In the figure in the upper right corner, we can see that the red line KDE is close to the N(0,1) red line, (where N(0,1)) is a normal distribution with mean 0 and standard deviation. This well shows that the residuals are normally distributed.
- The qq chart at the bottom left shows that the residual (blue dot) distribution follows from the standard normal distribution. Similarly, it shows that the residual is normally distributed.
- The residuals over time (top left) do not show any significant seasonal changes, but white noise. This is confirmed by the autocorrelation (i.e. correlation diagram) at the bottom right, which shows that the time series residuals have low correlation.
These observations lead us to conclude that our model produces a satisfactory fit, which can help us understand time series data and predict future value.
Although we have a satisfactory fit, some parameters of the seasonal ARIMA model can be changed to improve the model fit. Therefore, if we expand the scope of grid search, we may find a better model.
Step 6 - validate forecast
We have obtained the model for the time series and can now use it to generate predictions. We first compare the predicted value with the actual value of the time series, which will help us understand the accuracy of the prediction.
pred_ci = pred.conf_int()
The above code indicates that the forecast starts from January 1998.
We can plot the actual and predicted values of CO2 time series and evaluate our effect.
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
plt.show()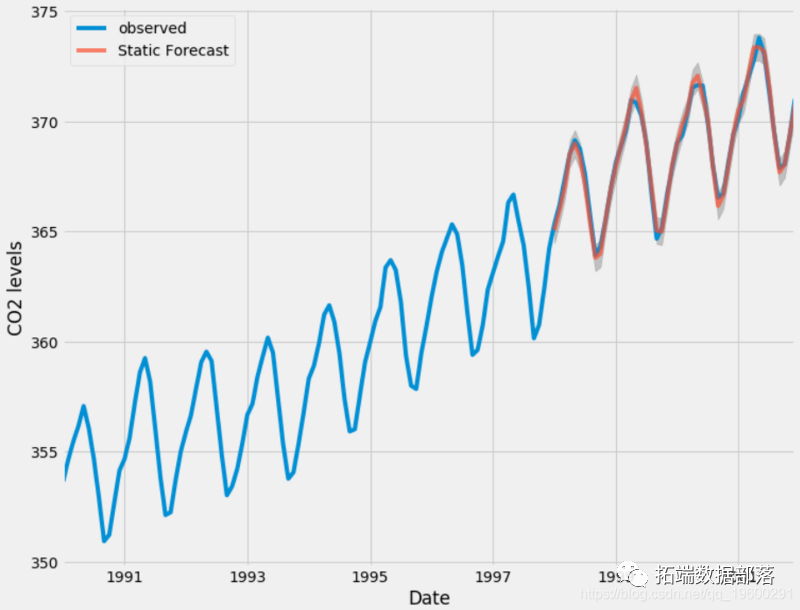
Overall, our forecast is in good agreement with the real value, showing an overall growth trend.
It is also useful to quantify our prediction accuracy. We will use MSE (mean square error) to summarize the average error of our prediction. For each predicted value, we calculate the difference from the real value and square the result. The results are squared, and the positive / negative differences do not offset each other when calculating the overall mean.
y_truth = y['1998-01-01':] # Calculated mean square error mse = ((y_forecasted - y_truth) ** 2).mean()
Output The mean square error of our prediction is 0.07
The MSE we predicted one step ahead yielded a value of 0.07, which is very low because it is close to 0. If MSE is 0, it is ideal to estimate the observations of the prediction parameters with ideal accuracy, but this is usually impossible.
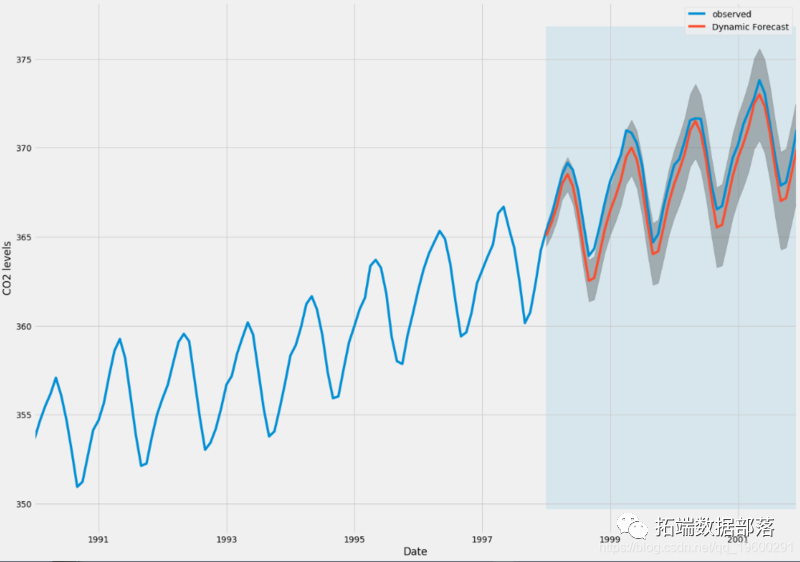
However, using dynamic prediction can better represent our real prediction ability. In this case, we only use the information in the time series up to a specific point, and then generate the prediction using the values in the previous prediction time point.
In the following code block, we specify that the dynamic prediction and confidence interval shall be calculated from January 1998.
By plotting the observed and predicted values of time series, we can see that the overall prediction is accurate even if dynamic prediction is used. All predicted values (red line) are very close to the real situation (blue line) and are within the confidence interval of our prediction.
Again, we quantify the effect of prediction by calculating MSE:
# Extract the predicted value and real value of time series
y_forecasted = pred_dynamic.predicted_mean
y_truth = y['1998-01-01':]
# Calculated mean square error
mse = ((y_forecasted - y_truth) ** 2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))Output The mean square error of our prediction is 1.01
The MSE generated from the predicted value obtained from the dynamic prediction is 1.01. This is slightly higher than the previous one, which can be expected because we rely on less historical data of time series.
Both one step ahead and dynamic prediction confirm that the time series model is effective. However, the interest of time series prediction is to predict the future value in advance.
Step 7 - generate and visualize predictions
Finally, we describe how to use seasonal ARIMA time series model to predict future data.
# Get predictions for the next 500 steps pred_uc = results.get_forecast(steps=500) # Get the confidence interval of the prediction pred_ci = pred_uc.conf_int()
We can use the output of this code to plot the time series and predict its future value.
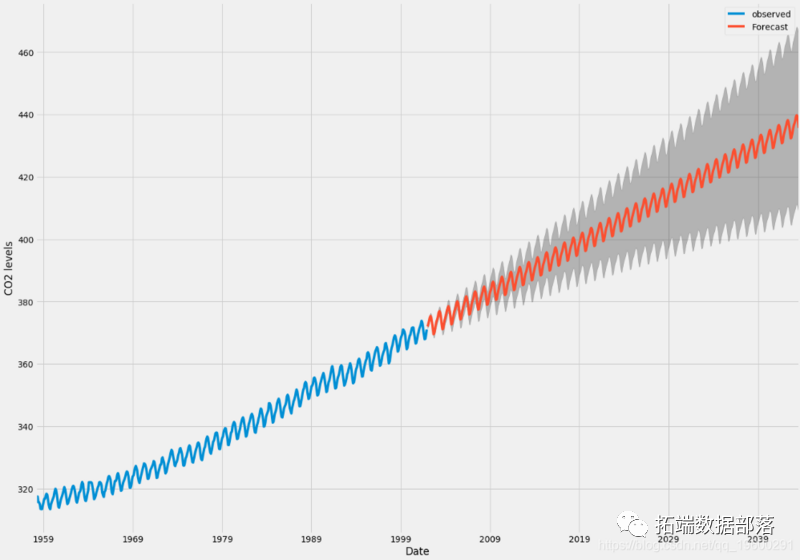
Now, the prediction and related confidence intervals we generated can be used to further understand the time series and predict the expected results. Our forecasts show that the time series is expected to continue to grow steadily.
As we further predict the future, the confidence interval will become larger and larger.
conclusion
In this tutorial, we described how to implement the seasonal ARIMA model in Python. It shows how to diagnose the model and how to generate the prediction of carbon dioxide time series.
You can try some other actions:
- Change the start date of the dynamic forecast to see how this affects the overall quality of the forecast.
- Try more parameter combinations to see if you can improve the goodness of fit of the model.
- Select other indicators and select the best model. For example, we use this AIC to find the best model.