1. Red black tree is a very important data structure with two obvious characteristics:
- The time complexity of insertion, deletion and search is close to O(logN). N is the number of nodes, which is significantly faster than the linked list; It is a binary tree with very stable performance!
- The results of middle order traversal are ordered from small to large
Based on the above two characteristics, red black tree is more suitable for application scenarios:
- Scenes requiring dynamic insertion, deletion and search include but are not limited to:
- Addition, deletion, modification and query of some databases, such as conditional retrieval such as select * from xxx where
- The processes in the linux kernel are organized and managed through the red black tree, which is easy to quickly insert, delete and find the tasks of the process_ struct
- Memory management in linux memory: allocation and recycling. Use the red black tree to organize the allocated memory blocks. When the application calls free to release memory, it can quickly find the target memory block in the red black tree according to the memory address
- The implementation of (key,value) adding, deleting and modifying query in hashmap; java 8 uses RBTree instead of linked list
- Ext3 file system, organize directory entries through red black tree
- Orderly scenes, such as:
- Implementation of linux timer: hrtimer is organized in the form of red black tree. The leftmost node of the tree is the timing with the fastest expiration
From the above application scenarios, we can see that the red black tree is a very popular data structure. Next, we will deeply analyze some typical scenarios to see how the linux kernel uses the red black tree!
2. Let's take a look at the definition of red black tree in include \ Linux \ rbtree H in the document:
struct rb_node { unsigned long __rb_parent_color; struct rb_node *rb_right; struct rb_node *rb_left; } __attribute__((aligned(sizeof(long)))); /* The alignment might seem pointless, but allegedly CRIS needs it */
The structure is very simple. There are only three fields. Anyone with a little development experience will have questions: there are so many application scenarios in red black tree, but there is no business field in one application scenario in this structure. It feels like a blank house that has not been decorated. How can this be used? This is precisely the subtlety of the design: the red black tree has a large number of application scenarios in the linux kernel_ The definition of node adds the business field of a specific application scenario, so this structure can only be used in this specific scenario. There is no universality at all, and it becomes a tightly coupled scenario; More such structures will increase the difficulty of subsequent code maintenance, so RB_ The definition of node structure is very simple, and only three attributes of the red black tree node itself are retained: left child, right child and node color (list_head structure is the same idea); How to use such a simple structure without business scenario attributes? Take a simple example to understand the principle of linux source code faster. For example, there are 50 students in a class, and each student has id, name and score scores. Now we need to organize all students with a red black tree. First define a student structure:
struct Student{ int id; char *name; int scroe struct rb_node s_rb; };
The first three are business fields, and the fourth is a red black tree field (the student and rb_node structures seem to be two separate structures, but the fields will be merged after being compiled by the compiler, resulting in a continuous memory, which is somewhat similar to the inheritance relationship of c + +); linux provides basic operations such as adding, deleting, modifying, checking, left-hand rotation, right-hand rotation and setting color of red black tree, as follows:
#define rb_parent(r) ((struct rb_node *)((r)->rb_parent_color & ~3)) //The lower two digits are cleared to 0 #define rb_color(r) ((r)->rb_parent_color & 1) //Take the last digit #define rb_is_red(r) (!rb_color(r)) //The last digit is 0? #define rb_is_black(r) rb_color(r) //The last digit is 1? #define rb_set_red(r) do { (r)->rb_parent_color &= ~1; } while (0) //Last position 0 #define rb_set_black(r) do { (r)->rb_parent_color |= 1; } while (0) //Last position 1 static inline void rb_set_parent(struct rb_node *rb, struct rb_node *p) //Set father { rb->rb_parent_color = (rb->rb_parent_color & 3) | (unsigned long)p; } static inline void rb_set_color(struct rb_node *rb, int color) //Set color { rb->rb_parent_color = (rb->rb_parent_color & ~1) | color; } //Left and right rotation void __rb_rotate_left(struct rb_node *node, struct rb_root *root); void __rb_rotate_right(struct rb_node *node, struct rb_root *root); //Delete node void rb_erase(struct rb_node *, struct rb_root *); void __rb_erase_color(struct rb_node *node, struct rb_node *parent, struct rb_root *root); //Replace node void rb_replace_node(struct rb_node *old, struct rb_node *new, struct rb_root *tree);void rb_link_node(struct rb_node * node, struct rb_node * parent, struct rb_node ** rb_link);
//Insert node//Traversing red black tree extern struct rb_node *rb_next(const struct rb_node *); //Successor extern struct rb_node *rb_prev(const struct rb_node *); //precursor extern struct rb_node *rb_first(const struct rb_root *);//minimum value extern struct rb_node *rb_last(const struct rb_root *); //Maximum
The parameters passed in by the above operation interface are rb_node, how can it be used to operate the red black tree of user-defined business scenarios, such as the student structure above? Since the incoming parameters of these interfaces are rb_node, if you do not change the parameters and function implementation, you can only pass RB as required by others_ Node parameter, how can the fields of the user-defined structure be added to the red black tree? This is also simple. Generate the structure by yourself, and then put the RB of the structure_ Pass in the node parameter as follows:
/* Add object to red black tree s_root Red black tree root node ptr_stu Object pointer rb_link The node where the object node is located rb_parent Parent node */ void student_link_rb(struct rb_root *s_root, struct Student *ptr_stu, struct rb_node **rb_link, struct rb_node *rb_parent) { rb_link_node(&ptr_stu->s_rb, rb_parent, rb_link); rb_insert_color(&ptr_stu->s_rb, s_root); } void add_student(struct rb_root *s_root, struct Student *stu, struct Student **stu_header) { struct rb_node **rb_link, *rb_parent; // Insert red black tree student_link_rb(s_root, stu, rb_link, rb_parent); }
If the score score is used as the key to construct the red black tree, the constructed tree is as follows: RB of each student node_ Right and Rb_ The left pointer points to RB_ The starting address of node, that is_ rb_ parent_ The value of color, but the values of score, name and id are actually the ones that need to be read and written in business. How can we get the values of these fields?
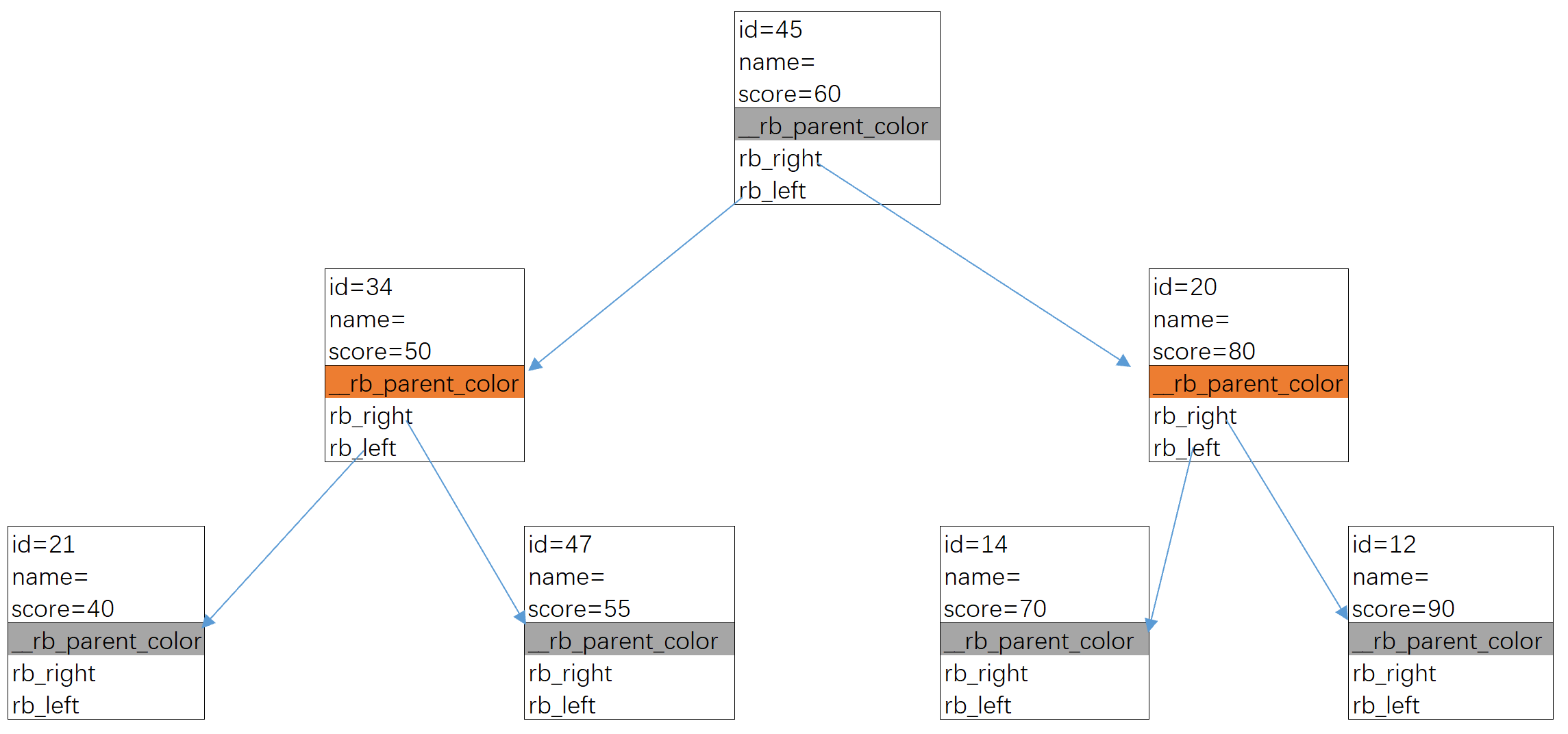
linux developers have already figured out how to read: first get the start address of the student instance, and then read the field by offset? As follows:
#define container_of(ptr, type, member) ({ \ const typeof( ((type *)0)->member ) *__mptr = (ptr); \ (type *)( (char *)__mptr - offsetof(type,member) );})
The first address of the student instance can be obtained through the above macro definition. The usage is as follows: call container_of method, pass in the instance of rbnode (confirm the location of student instance), student structure and internal RB_ Node position (used to calculate rb_node offset inside the structure, and then deduce the first address of the student instance): get the first address of the student instance, and then you can use id, name, score and other fields directly;
struct Student* find_by_id(struct rb_root *root, int id) { struct Student *ptr_stu = NULL; struct rb_node *rbnode = root->rb_node; while (NULL != rbnode) { //The core code: when the three parameters are rb_node Examples of, student Structure definition and internal rb_node Field location struct Student *ptr_tmp = container_of(rbnode, struct Student, s_rb); if (id < ptr_tmp->id) { rbnode = rbnode->rb_left; } else if (id > ptr_tmp->id) { rbnode = rbnode->rb_right; } else { ptr_stu = ptr_tmp; break; } } return ptr_stu; }
Summarize the general process of using red black tree:
- The developer defines the fields of the structure according to the requirements of the business scenario, which must include rb_node;
- Generate an instance stu of the structure and call rb_link_node add nodes to build a red black tree. Of course, the parameter passed in is stu - > s_ rb
- When traversing the search, find s according to_ RB instance, custom structure, rb_node gets the first address of the custom structure instance from the name of the structure, and then you can happily read and write the business field!
3. The above case is simple enough. The principle of using red black tree in various complex scenarios in linux is the same as this one, and there is no essential difference! If you understand the principle of the above case, you will understand the principle of using red black tree in linux kernel! Next, let's look at some shutdown api implementation methods of red black tree:
(1) red black trees are arranged in good order, and the results of middle order traversal are arranged from small to large; The leftmost node is the smallest node of the whole tree, so you can find the first and smallest node all the way to the left;
/* * This function returns the first node (in sort order) of the tree. */ struct rb_node *rb_first(const struct rb_root *root) { struct rb_node *n; n = root->rb_node; if (!n) return NULL; while (n->rb_left) n = n->rb_left; return n; }
Similarly: you can find the largest node of the whole tree all the way to the right
struct rb_node *rb_last(const struct rb_root *root) { struct rb_node *n; n = root->rb_node; if (!n) return NULL; while (n->rb_right) n = n->rb_right; return n; }
(2) find the next node of A node: for example, if the value of node A is 50, start from the right child of node A (all nodes of the right child are larger than A), and look to the left for as far as get null; That is, the smallest node larger than A in the whole tree; This function can be used for conditional query!
struct rb_node *rb_next(const struct rb_node *node) { struct rb_node *parent; if (RB_EMPTY_NODE(node)) return NULL; /* * If we have a right-hand child, go down and then left as far * as we can. */ if (node->rb_right) { node = node->rb_right; while (node->rb_left) node=node->rb_left; return (struct rb_node *)node; } /* * No right-hand children. Everything down and left is smaller than us, * so any 'next' node must be in the general direction of our parent. * Go up the tree; any time the ancestor is a right-hand child of its * parent, keep going up. First time it's a left-hand child of its * parent, said parent is our 'next' node. */ while ((parent = rb_parent(node)) && node == parent->rb_right) node = parent; return parent; }
Similarly, find the largest node smaller than A in the whole tree:
struct rb_node *rb_prev(const struct rb_node *node) { struct rb_node *parent; if (RB_EMPTY_NODE(node)) return NULL; /* * If we have a left-hand child, go down and then right as far * as we can. */ if (node->rb_left) { node = node->rb_left; while (node->rb_right) node=node->rb_right; return (struct rb_node *)node; } /* * No left-hand children. Go up till we find an ancestor which * is a right-hand child of its parent. */ while ((parent = rb_parent(node)) && node == parent->rb_left) node = parent; return parent; }
(3) replace a node: change the direction of the surrounding pointer, and then change the node color
void rb_replace_node(struct rb_node *victim, struct rb_node *new, struct rb_root *root) { struct rb_node *parent = rb_parent(victim); /* Set the surrounding nodes to point to the replacement */ __rb_change_child(victim, new, parent, root); if (victim->rb_left) rb_set_parent(victim->rb_left, new); if (victim->rb_right) rb_set_parent(victim->rb_right, new); /* Copy the pointers/colour from the victim to the replacement */ *new = *victim; }
(4) insert a node: rotate left and right in different situations;
static __always_inline void __rb_insert(struct rb_node *node, struct rb_root *root, void (*augment_rotate)(struct rb_node *old, struct rb_node *new)) { struct rb_node *parent = rb_red_parent(node), *gparent, *tmp; while (true) { /* * Loop invariant: node is red * * If there is a black parent, we are done. * Otherwise, take some corrective action as we don't * want a red root or two consecutive red nodes. */ if (!parent) { rb_set_parent_color(node, NULL, RB_BLACK); break; } else if (rb_is_black(parent)) break; gparent = rb_red_parent(parent); tmp = gparent->rb_right; if (parent != tmp) { /* parent == gparent->rb_left */ if (tmp && rb_is_red(tmp)) { /* * Case 1 - color flips * * G g * / \ / \ * p u --> P U * / / * n n * * However, since g's parent might be red, and * 4) does not allow this, we need to recurse * at g. */ rb_set_parent_color(tmp, gparent, RB_BLACK); rb_set_parent_color(parent, gparent, RB_BLACK); node = gparent; parent = rb_parent(node); rb_set_parent_color(node, parent, RB_RED); continue; } tmp = parent->rb_right; if (node == tmp) { /* * Case 2 - left rotate at parent * * G G * / \ / \ * p U --> n U * \ / * n p * * This still leaves us in violation of 4), the * continuation into Case 3 will fix that. */ tmp = node->rb_left; WRITE_ONCE(parent->rb_right, tmp); WRITE_ONCE(node->rb_left, parent); if (tmp) rb_set_parent_color(tmp, parent, RB_BLACK); rb_set_parent_color(parent, node, RB_RED); augment_rotate(parent, node); parent = node; tmp = node->rb_right; } /* * Case 3 - right rotate at gparent * * G P * / \ / \ * p U --> n g * / \ * n U */ WRITE_ONCE(gparent->rb_left, tmp); /* == parent->rb_right */ WRITE_ONCE(parent->rb_right, gparent); if (tmp) rb_set_parent_color(tmp, gparent, RB_BLACK); __rb_rotate_set_parents(gparent, parent, root, RB_RED); augment_rotate(gparent, parent); break; } else { tmp = gparent->rb_left; if (tmp && rb_is_red(tmp)) { /* Case 1 - color flips */ rb_set_parent_color(tmp, gparent, RB_BLACK); rb_set_parent_color(parent, gparent, RB_BLACK); node = gparent; parent = rb_parent(node); rb_set_parent_color(node, parent, RB_RED); continue; } tmp = parent->rb_left; if (node == tmp) { /* Case 2 - right rotate at parent */ tmp = node->rb_right; WRITE_ONCE(parent->rb_left, tmp); WRITE_ONCE(node->rb_right, parent); if (tmp) rb_set_parent_color(tmp, parent, RB_BLACK); rb_set_parent_color(parent, node, RB_RED); augment_rotate(parent, node); parent = node; tmp = node->rb_left; } /* Case 3 - left rotate at gparent */ WRITE_ONCE(gparent->rb_right, tmp); /* == parent->rb_left */ WRITE_ONCE(parent->rb_left, gparent); if (tmp) rb_set_parent_color(tmp, gparent, RB_BLACK); __rb_rotate_set_parents(gparent, parent, root, RB_RED); augment_rotate(gparent, parent); break; } } }
rb_ The most awesome thing about node: it removes the fields of business attributes and is loosely coupled with the business scenario, making RB_ The node structure and corresponding methods can be used in different business scenarios; At the same time, cooperate with the container_of function, which can be passed through rb_node instance address quickly reverses the first address of the business structure instance to facilitate reading and writing business attribute fields. This approach is high! It's really high!
reference resources:
1, https://www.bilibili.com/video/BV135411h7wJ?p=1 Introduction to red black tree
2, https://cloud.tencent.com/developer/article/1922776 Data structure red black tree
3, https://blog.csdn.net/weixin_46381158/article/details/117999284 Basic usage of red black tree
4, https://rbtree.phpisfuture.com/ Red black tree online demonstration