Image processing evaluation index_ PSNR peak signal-to-noise ratio
PSNR
psnr is the abbreviation of "Peak Signal to Noise Ratio", that is, peak signal-to-noise ratio. It is an objective standard for evaluating images. In order to measure the image quality after processing, we usually refer to the PSNR value to measure whether a processing program is satisfactory. The unit of PSNR is dB. The larger the value, the smaller the distortion. N is the number of bits per pixel. The general gray image takes 8, that is, the gray scale number of pixels is 256. It is the logarithm of the mean square error between the original image and the processed image relative to (2n-1)2 (the square of the maximum value of the signal, and N is the number of bits of each sampling value). Therefore, the larger the PSNR value, the less distortion. The formula of MATLAB usage is as follows:
PSNR=10*log10((2n-1)2/MSE)
Where MSE is the mean square error between the original image and the processed image.
Advantages and disadvantages
PSNR is the most common and widely used objective measure to evaluate image quality. However, many experimental results show that the score of PSNR cannot be completely consistent with the visual quality seen by human eyes. It is possible that those with higher PSNR look worse than those with lower PSNR. This is because the sensitivity of human vision to error is not absolute, and its perception results will be affected by many factors (for example, human eyes are more sensitive to contrast differences with lower spatial frequency, human eyes are more sensitive to brightness contrast differences than chromaticity, and human eyes' perception results of an area will be affected by its surrounding adjacent areas).
Matlab code
function [PSNR, MSE] = psnr(X, Y)
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% Calculate peak signal-to-noise ratio PSNR
% take RGB Turn into YCbCr Format for calculation
% If calculated directly, it will be 2 less than the calculated value after rotation dB Left and right (individual test, of course)
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%
if size(X,3)~=1 %When judging the image, it is not a color image. If yes, the result is 3, otherwise it is 1
org=rgb2ycbcr(X);
test=rgb2ycbcr(Y);
Y1=org(:,:,1);
Y2=test(:,:,1);
Y1=double(Y1); %When calculating the square, it needs to be converted into double Type, otherwise uchar Type will lose data
Y2=double(Y2);
else %Grayscale image, no conversion
Y1=double(X);
Y2=double(Y);
end
if nargin<2
D = Y1;
else
if any(size(Y1)~=size(Y2))
error('The input size is not equal to each other!');
end
D = Y1 - Y2;
end
MSE = sum(D(:).*D(:)) / numel(Y1);
PSNR = 10*log10(255^2 / MSE);SSIM
SSIM(structural similarity index), structural similarity, is an index to measure the similarity of two images. The index was first proposed by the laboratory for image and video engineering of the University of Texas at Austin. Among the two images used by SSIM, one is an uncompressed undistorted image and the other is a distorted image.
Given two images x and y, the structural similarity of the two images can be obtained in the following way
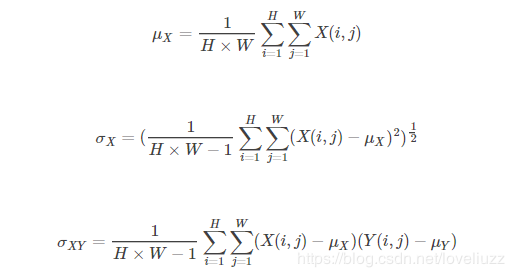
Among them, μ_ X, μ_ Y represents the mean value of image X and Y respectively, σ_ X, σ_ Y represents the variance of images X and y, respectively, σ_ XY represents the covariance of images X and y.
SSIM measures image similarity from three aspects: brightness, contrast and structure.
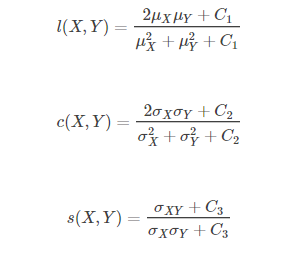
C1, C2 and C3 are constants. In order to avoid the denominator being 0, C1=(K1 * L)2, C2=(K2 * L)2, C3=C22, generally K1 = 0.01, K2 = 0.03 and L = 255,
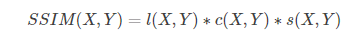
Matlab formula
function [ssimval, ssimmap] = ssim(varargin)
%SSIM Structural Similarity Index for measuring image quality
% SSIMVAL = SSIM(A, REF) calculates the Structural Similarity Index
% (SSIM) value for image A, with the image REF as the reference. A and
% REF can be 2D grayscale or 3D volume images, and must be of the same
% size and class.
%
% [SSIMVAL, SSIMMAP] = SSIM(A, REF) also returns the local SSIM value for
% each pixel in SSIMMAP. SSIMMAP has the same size as A.
%
% [SSIMVAL, SSIMMAP] = SSIM(A, REF, NAME1, VAL1,...) calculates the SSIM
% value using name-value pairs to control aspects of the computation.
% Parameter names can be abbreviated.
%
% Parameters include:
%
% 'Radius' - Specifies the standard deviation of
% isotropic Gaussian function used for
% weighting the neighborhood pixels around a
% pixel for estimating local statistics. This
% weighting is used to avoid blocking
% artifacts in estimating local statistics.
% The default value is 1.5.
%
% 'DynamicRange' - Positive scalar, L, that specifies the
% dynamic range of the input image. By
% default, L is chosen based on the class of
% the input image A, as L =
% diff(getrangefromclass(A)). Note that when
% class of A is single or double, L = 1 by
% default.
%
% 'RegularizationConstants'- Three-element vector, [C1 C2 C3], of
% non-negative real numbers that specifies the
% regularization constants for the luminance,
% contrast, and structural terms (see [1]),
% respectively. The regularization constants
% are used to avoid instability for image
% regions where the local mean or standard
% deviation is close to zero. Therefore, small
% non-zero values should be used for these
% constants. By default, C1 = (0.01*L).^2, C2
% = (0.03*L).^2, and C3 = C2/2, where L is the
% specified 'DynamicRange' value. If a value
% of 'DynamicRange' is not specified, the
% default value is used (see name-value pair
% 'DynamicRange').
%
% 'Exponents' - Three-element vector [alpha beta gamma],
% of non-negative real numbers that specifies
% the exponents for the luminance, contrast,
% and structural terms (see [1]),
% respectively. By default, all the three
% exponents are 1, i.e. the vector is [1 1
% 1].
%
% Notes
% -----
% 1. A and REF can be arrays of upto three dimensions. All 3D arrays
% are considered 3D volumetric images. RGB images will also be
% processed as 3D volumetric images.
%
% 2. Input image A and reference image REF are converted to
% floating-point type for internal computation.
%
% 3. For signed-integer images (int16), an offset is applied to bring the
% gray values in the non-negative range before computing the SSIM
% index.
%
% Example
% ---------
% This example shows how to compute SSIM value for a blurred image given
% the original reference image.
%
% ref = imread('pout.tif');
% H = fspecial('Gaussian',[11 11],1.5);
% A = imfilter(ref,H,'replicate');
%
% subplot(1,2,1); imshow(ref); title('Reference Image');
% subplot(1,2,2); imshow(A); title('Blurred Image');
%
% [ssimval, ssimmap] = ssim(A,ref);
%
% fprintf('The SSIM value is %0.4f.\n',ssimval);
%
% figure, imshow(ssimmap,[]);
% title(sprintf('SSIM Index Map - Mean SSIM Value is %0.4f',ssimval));
% Class Support
% -------------
% Input arrays A and REF must be one of the following classes: uint8,
% int16, uint16, single, or double. Both A and REF must be of the same
% class. They must be nonsparse. SSIMVAL is a scalar and SSIMMAP is an
% array of the same size as A. Both SSIMVAL and SSIMMAP are of class
% double, unless A and REF are of class single in which case SSIMVAL and
% SSIMMAP are of class single.
%
% References:
% -----------
% [1] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image
% Quality Assessment: From Error Visibility to Structural
% Similarity," IEEE Transactions on Image Processing, Volume 13,
% Issue 4, pp. 600- 612, 2004.
%
% See also IMMSE, MEAN, MEDIAN, PSNR, SUM, VAR.
% Copyright 2013-2014 The MathWorks, Inc.
narginchk(2,10);
[A, ref, C, exponents, radius] = parse_inputs(varargin{:});
if isempty(A)
ssimval = zeros(0, 'like', A);
ssimmap = A;
return;
end
if isa(A,'int16') % int16 is the only allowed signed-integer type for A and ref.
% Add offset for signed-integer types to bring values in the
% non-negative range.
A = double(A) - double(intmin('int16'));
ref = double(ref) - double(intmin('int16'));
elseif isinteger(A)
A = double(A);
ref = double(ref);
end
% Gaussian weighting function
gaussFilt = getGaussianWeightingFilter(radius,ndims(A));
% Weighted-mean and weighted-variance computations
mux2 = imfilter(A, gaussFilt,'conv','replicate');
muy2 = imfilter(ref, gaussFilt,'conv','replicate');
muxy = mux2.*muy2;
mux2 = mux2.^2;
muy2 = muy2.^2;
sigmax2 = imfilter(A.^2,gaussFilt,'conv','replicate') - mux2;
sigmay2 = imfilter(ref.^2,gaussFilt,'conv','replicate') - muy2;
sigmaxy = imfilter(A.*ref,gaussFilt,'conv','replicate') - muxy;
% Compute SSIM index
if (C(3) == C(2)/2) && isequal(exponents(:),ones(3,1))
% Special case: Equation 13 from [1]
num = (2*muxy + C(1)).*(2*sigmaxy + C(2));
den = (mux2 + muy2 + C(1)).*(sigmax2 + sigmay2 + C(2));
if (C(1) > 0) && (C(2) > 0)
ssimmap = num./den;
else
% Need to guard against divide-by-zero if either C(1) or C(2) is 0.
isDenNonZero = (den ~= 0);
ssimmap = ones(size(A));
ssimmap(isDenNonZero) = num(isDenNonZero)./den(isDenNonZero);
end
else
% General case: Equation 12 from [1]
% Luminance term
if (exponents(1) > 0)
num = 2*muxy + C(1);
den = mux2 + muy2 + C(1);
ssimmap = guardedDivideAndExponent(num,den,C(1),exponents(1));
else
ssimmap = ones(size(A), 'like', A);
end
% Contrast term
sigmaxsigmay = [];
if (exponents(2) > 0)
sigmaxsigmay = sqrt(sigmax2.*sigmay2);
num = 2*sigmaxsigmay + C(2);
den = sigmax2 + sigmay2 + C(2);
ssimmap = ssimmap.*guardedDivideAndExponent(num,den,C(2),exponents(2));
end
% Structure term
if (exponents(3) > 0)
num = sigmaxy + C(3);
if isempty(sigmaxsigmay)
sigmaxsigmay = sqrt(sigmax2.*sigmay2);
end
den = sigmaxsigmay + C(3);
ssimmap = ssimmap.*guardedDivideAndExponent(num,den,C(3),exponents(3));
end
end
ssimval = mean(ssimmap(:));
end
% -------------------------------------------------------------------------
function component = guardedDivideAndExponent(num, den, C, exponent)
if C > 0
component = num./den;
else
component = ones(size(num),'like',num);
isDenNonZero = (den ~= 0);
component(isDenNonZero) = num(isDenNonZero)./den(isDenNonZero);
end
if (exponent ~= 1)
component = component.^exponent;
end
end
function gaussFilt = getGaussianWeightingFilter(radius,N)
% Get 2D or 3D Gaussian weighting filter
filtRadius = ceil(radius*3); % 3 Standard deviations include >99% of the area.
filtSize = 2*filtRadius + 1;
if (N < 3)
% 2D Gaussian mask can be used for filtering even one-dimensional
% signals using imfilter.
gaussFilt = fspecial('gaussian',[filtSize filtSize],radius);
else
% 3D Gaussian mask
[x,y,z] = ndgrid(-filtRadius:filtRadius,-filtRadius:filtRadius, ...
-filtRadius:filtRadius);
arg = -(x.*x + y.*y + z.*z)/(2*radius*radius);
gaussFilt = exp(arg);
gaussFilt(gaussFilt<eps*max(gaussFilt(:))) = 0;
sumFilt = sum(gaussFilt(:));
if (sumFilt ~= 0)
gaussFilt = gaussFilt/sumFilt;
end
end
end
function [A, ref, C, exponents, radius] = parse_inputs(varargin)
validImageTypes = {'uint8','uint16','int16','single','double'};
A = varargin{1};
validateattributes(A,validImageTypes,{'nonsparse','real'},mfilename,'A',1);
ref = varargin{2};
validateattributes(ref,validImageTypes,{'nonsparse','real'},mfilename,'REF',2);
if ~isa(A,class(ref))
error(message('images:validate:differentClassMatrices','A','REF'));
end
if ~isequal(size(A),size(ref))
error(message('images:validate:unequalSizeMatrices','A','REF'));
end
if (ndims(A) > 3)
error(message('images:validate:tooManyDimensions','A and REF',3));
end
% Default values for parameters
dynmRange = diff(getrangefromclass(A));
C = [];
exponents = [1 1 1];
radius = 1.5;
args_names = {'dynamicrange', 'regularizationconstants','exponents',...
'radius'};
for i = 3:2:nargin
arg = varargin{i};
if ischar(arg)
idx = find(strncmpi(arg, args_names, numel(arg)));
if isempty(idx)
error(message('images:validate:unknownInputString', arg))
elseif numel(idx) > 1
error(message('images:validate:ambiguousInputString', arg))
elseif numel(idx) == 1
if (i+1 > nargin)
error(message('images:validate:missingParameterValue'));
end
if idx == 1
dynmRange = varargin{i+1};
validateattributes(dynmRange,{'numeric'},{'positive', ...
'finite', 'real', 'nonempty','scalar'}, mfilename, ...
'DynamicRange',i);
dynmRange = double(dynmRange);
elseif idx == 2
C = varargin{i+1};
validateattributes(C,{'numeric'},{'nonnegative','finite', ...
'real','nonempty','vector', 'numel', 3}, mfilename, ...
'RegularizationConstants',i);
C = double(C);
elseif idx == 3
exponents = varargin{i+1};
validateattributes(exponents,{'numeric'},{'nonnegative', ...
'finite', 'real', 'nonempty','vector', 'numel', 3}, ...
mfilename,'Exponents',i);
exponents = double(exponents);
elseif idx == 4
radius = varargin{i+1};
validateattributes(radius,{'numeric'},{'positive','finite', ...
'real', 'nonempty','scalar'}, mfilename,'Radius',i);
radius = double(radius);
end
end
else
error(message('images:validate:mustBeString'));
end
end
% If 'RegularizationConstants' is not specified, choose default C.
if isempty(C)
C = [(0.01*dynmRange).^2 (0.03*dynmRange).^2 ((0.03*dynmRange).^2)/2];
end
end