**
Infix to suffix expression
**
1, Suffix expression evaluation
The suffix expression is also called inverse Polish expression, and its evaluation process can use the stack to assist storage. Assuming that the suffix expression to be evaluated is 6 5 2 3 + 8 * + 3 + *, the evaluation process is as follows:
1) When traversing the expression, the numbers encountered are first put into the stack. At this time, the stack is as follows:
2) Then read "+", pop up 3 and 2, execute 3 + 2, the calculation result is equal to 5, and press 5 into the stack.
3) Read 8 and put it directly on the stack.
4) After reading "", pop up 8 and 5, execute 85, and press the result 40 into the stack. Then the process is similar. Read "+", pop up 40 and 5, press the result 45 of 40 + 5 onto the stack... And so on. The final value is 288.
2, Infix expression to suffix expression
2.1) Rules
Infix expression a + b*c + (d * e + f) * g, which is converted to suffix expression a b c * + d e * f + g * +.
Stack is required in the conversion process. The specific process is as follows:
1) If we encounter operands, we output them directly.
2) If we encounter an operator, we put it on the stack, and when we encounter an open bracket, we also put it on the stack.
3) If a right parenthesis is encountered, the stack element will be popped, and the popped operator will be output until the left parenthesis is is encountered. Note that the left parenthesis only pops up and does not output.
4) If you encounter any other operators, such as "+", "*", "("), pop the element from the stack until you find a lower priority element (or the stack is empty). After popping these elements, the encountered operators are pushed onto the stack. It should be noted that we will pop up only when we encounter a ")" ("", and we will not pop up in other cases "(" ".
5) If we read the end of the input, all the elements in the stack will pop up in turn.
2.2) examples
There are many rules, but it is easier to explain the whole process with examples. Take the above conversion as an example, the input is a + b * c + (d * e + f)*g, and the processing process is as follows:
1) First read a and output directly.
2) Read "+" and put it on the stack.
3) Read b and output directly.
The stack and output are as follows:
4) Read "*", because the "+" priority of the top element of the stack is lower than "*", press "*" directly into the stack.
5) Read c and output directly.
The stack and output are as follows:
6) When reading "+", because the top element "*" has higher priority than it, it pops up "*" and outputs it. Similarly, the next element "+" in the stack has the same priority as the read operator "+", so it also pops up and outputs it. Then press the read "+" into the stack.
The stack and output are as follows:
7) The next read is "(", which has the highest priority, so it is directly put into the stack.
8) Read d and output it directly.
The stack and output are as follows:
9) When reading "*", the "*" is directly pushed into the stack because the left parenthesis "(" will pop up only when it meets ")".
10) Read e and output directly.
The stack and output are as follows:
11) Read "+", pop up "*" and output it, and then press "+" into the stack.
12) Read f and output directly.
Stack and output conditions:
13) Next, when you read ")", you will directly pop up the elements in the stack and output them until you encounter "(". Here, only one operator "+" before the right bracket is popped up and output.
14) Read "*" and press it into the stack. Read g and output directly.
15) At this time, the input data has been read to the end, and there are two operators "*" and "+" in the stack, which pop up and output directly.
So far, the whole conversion process is completed. The program implementation code is supplemented later.
2.3) another method of conversion
1) First, parenthesize the infix expression according to the priority of the operator to become ((a + (BC)) + (((DE) + F) * g))
2) Move the operator to the end of the bracket and become ((a (BC) * + (((DE) f) + G))+
3) Remove the brackets and get abc*+def+g+
code:
package P2.linear structure;
//Infix expression to suffix expression
public class InfixToSuffix {
public static void main(String[] args) {
String expression = "(10+20/2*3)/2+8";
expression = infixToSuffix(expression);
System.out.println(expression);
}
public static String infixToSuffix(String expression) {
//Stack of operators
ArrayStack<String> opStack = new ArrayStack<>();
//Linear table of suffix expression
ArrayList<String> suffixList = new ArrayList<>();
//Format expression
expression = insertBlanks(expression);
String[] tokens = expression.split(" ");
for (String token : tokens) {
//Filter empty string
if (token.length() == 0) {
continue;
}
//Judgment operator + - */
if (isOperator(token)) {
/*
When do operators stack?
1.If the stack is empty
2.If the top of the stack is(
3.If the top of the stack is an operator and the priority is lower than the current token
When do I need to get the top operator out of the stack?
1.Priority of stack top operator > = current token
*/
while (true) {
if (opStack.isEmpty() || opStack.element().equals("(") || priority(opStack.element()) < priority(token)) {
opStack.push(token);
break;
}
suffixList.add(opStack.pop());
}
} else if (token.equals("(")) {
opStack.push(token);
} else if (token.equals(")")) {
while (!opStack.element().equals("(")) {
suffixList.add(opStack.pop());
}
opStack.pop();
} else if (isNumber(token)) {
suffixList.add(token);
} else {
throw new IllegalArgumentException("wrong char :" + expression);
}
}
while (!opStack.isEmpty()) {
suffixList.add(opStack.pop());
}
//Splice numeric elements and operator elements
StringBuilder sb = new StringBuilder();
for (int i = 0; i < suffixList.size(); i++) {
sb.append(suffixList.get(i));
sb.append(' ');
}
return sb.toString();
}
private static int priority(String token) {
if (token.equals("+") || token.equals("-")) {
return 0;
}
if (token.equals("*") || token.equals("/")) {
return 1;
}
return -1;
}
private static boolean isNumber(String token) {
return token.matches("\\d+");
}
private static boolean isOperator(String token) {
return token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/");
}
//Format the original expression and add spaces around all non numeric characters
private static String insertBlanks(String expression) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < expression.length(); i++) {
char c = expression.charAt(i);
if (c == '(' || c == ')' || c == '+' || c == '-' || c == '*' || c == '/') {
sb.append(' ');
sb.append(c);
sb.append(' ');
} else {
sb.append(c);
}
}
return sb.toString();
}
}
Suffix expression calculator
package P2.linear structure;
//Suffix expression calculator
public class SuffixCalculator {
public static void main(String[] args) {
String infixExpression = "(10+20/2*3)/2+8";
String suffixExpression = InfixToSuffix.infixToSuffix(infixExpression);
int result = evaluateSuffix(suffixExpression);
System.out.println(result);
}
private static int evaluateSuffix(String suffixExpression) {
ArrayStack<Integer> stack = new ArrayStack<>();
String[] tokens = suffixExpression.split(" ");
for(String token : tokens){
if(token.length() == 0){
continue;
}
if(isNumber(token)){
stack.push(new Integer(token));
}else {
processAnOperator(stack,token);
}
}
return stack.pop();
}
private static void processAnOperator(ArrayStack<Integer> stack, String token) {
int num1 = stack.pop();
int num2 = stack.pop();
if (token.equals("+")) {
stack.push(num2 + num1);
} else if (token.equals("-")) {
stack.push(num2 - num1);
} else if (token.equals("*")) {
stack.push(num2 * num1);
} else if (token.equals("/")) {
stack.push(num2 / num1);
}
}
private static boolean isNumber(String token) {
return token.matches("\\d+");
}
}
**
Double ended stack
**
I Definition of stack
A stack is a linear table that is restricted to insert and delete operations only at the end of the table.
We call the end that allows insertion and deletion the top of the stack and the other end the bottom of the stack.
A stack without any data elements is called an empty stack.
In daily life, the loading of bullets is an example of a stack. Bullets are pressed in one by one, just like entering the stack, and shot out one by one, just like leaving the stack.
Enter the stack
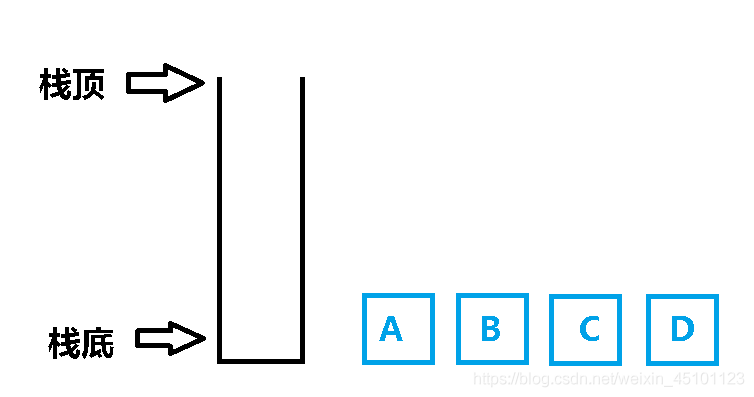
Empty stack, element not on stack
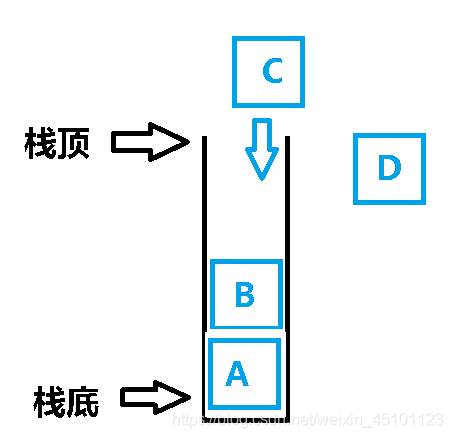
The elements are stacked in turn, and the first element is pushed to the bottom of the stack.
Out of stack
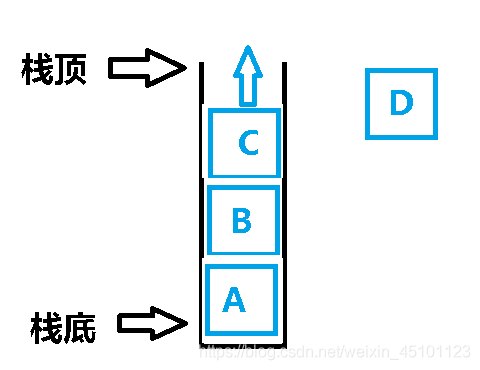
The elements at the top of the stack are out of the stack first, and the elements at the bottom of the stack are out of the stack last, that is, the elements that enter first are out of the stack last, just like the magazine of bullets in real life.
code:
package P2.linear structure;
import java.util.Iterator;
//Double ended stack
public class ArrayDoubleEndStack<E> implements Iterable<E> {
//Top of left stack
private int ltop;
//Top of right stack
private int rtop;
//Container for storing elements
private E[] data;
//Default capacity of array container
private static int DEFAULT_CAPACITY = 10;
public ArrayDoubleEndStack() {
data = (E[]) new Object[DEFAULT_CAPACITY];
ltop = -1;
rtop = data.length;
}
public void pushLeft(E element) {
if (ltop + 1 == rtop) {
resize(data.length * 2);
}
data[++ltop] = element;
}
public void pushRight(E element) {
if (ltop + 1 == rtop) {
resize(data.length * 2);
}
data[--rtop] = element;
}
private void resize(int newLen) {
E[] newData = (E[]) new Object[newLen];
//Copy the elements of the left stack
for (int i = 0; i <= ltop; i++) {
newData[i] = data[i];
}
//Copy the elements of the right stack
int index = rtop;
for (int i = newLen - sizeRight(); i < newLen; i++) {
newData[i] = data[index++];
}
rtop = newLen - sizeRight();
data = newData;
}
public E popLeft() {
if (isLeftEmpty()) {
throw new IllegalArgumentException("left stack is null");
}
E ret = data[ltop--];
if (sizeLeft() + sizeRight() <= data.length / 4 && data.length > DEFAULT_CAPACITY) {
resize(data.length / 2);
}
return ret;
}
public E popRight() {
if (isRightEmpty()) {
throw new IllegalArgumentException("right stack is null");
}
E ret = data[rtop++];
if (sizeLeft() + sizeRight() <= data.length / 4 && data.length > DEFAULT_CAPACITY) {
resize(data.length / 2);
}
return ret;
}
public E peekLeft() {
if (isLeftEmpty()) {
throw new IllegalArgumentException("left stack is null");
}
return data[ltop];
}
public E peekRight() {
if (isRightEmpty()) {
throw new IllegalArgumentException("right stack is null");
}
return data[rtop];
}
public boolean isLeftEmpty() {
return ltop == -1;
}
public boolean isRightEmpty() {
return rtop == data.length;
}
public int sizeLeft() {
return ltop + 1;
}
public int sizeRight() {
return data.length - rtop;
}
@Override
public String toString() {
// 1 2 3 7 8 9
StringBuilder sb = new StringBuilder();
sb.append('[');
if (isLeftEmpty() && isRightEmpty()) {
sb.append(']');
return sb.toString();
}
//Start on the left
for (int i = 0; i <= ltop; i++) {
sb.append(data[i]);
if (i == ltop && isRightEmpty()) {
sb.append(']');
return sb.toString();
} else {
sb.append(',');
}
}
//Back right
for (int i = rtop; i < data.length; i++) {
sb.append(data[i]);
if (i == data.length - 1) {
sb.append(']');
} else {
sb.append(',');
}
}
return sb.toString();
}
@Override
public Iterator<E> iterator() {
return new ArrayDoubleEndStackIterator();
}
class ArrayDoubleEndStackIterator implements Iterator<E> {
private ArrayList<E> list;
private Iterator<E> it;
public ArrayDoubleEndStackIterator() {
list = new ArrayList<>();
for (int i = 0; i <= ltop; i++) {
list.add(data[i]);
}
for (int i = rtop; i < data.length; i++) {
list.add(data[i]);
}
it = list.iterator();
}
@Override
public boolean hasNext() {
return it.hasNext();
}
@Override
public E next() {
return it.next();
}
}
}