I

Bailian 4116 rescue operation( OpenJudge - 4116: rescue operations)

This problem is to add a guard on the basis of simple BFS. Killing a guard also needs + 1. Others can follow the idea of ordinary BFS as usual. The most important thing is that killing a guard can be regarded as a point after twice, so there is no need to deal with killing a guard with time + 2. The difference between this question and the following two questions is that the guard killed by another path (because BFS is searched by many paths at the same time) does not have to be killed in another path (if the guard has been killed, there must be another path shorter than the current path, so there is no need to go this way) If you understand this, draw a picture to distinguish the differences between these questions arbitrarily.

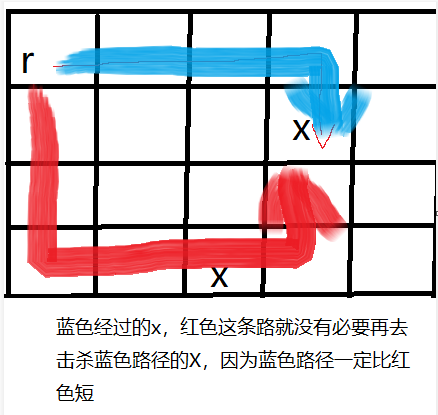
First explain how to kill the guard as two times. After passing through this point, look at the picture first

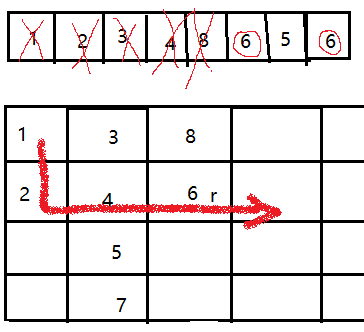
struct point{
    int x;
    int y;
    int step;
    int flag;
    point(int a,int b,int c,int d):x(a),y(b),step(c),flag(d){}
    point(){}
};

First, use flag to mark whether the current position is a guard.

if(u.flag==1)
{
     r.push(point(u.x,u.y,u.step+1,0));
     continue;
}

When the flag of the current position = = 1, the current point will be added to the team again (as shown in the above figure), which is equivalent to walking this position twice.

The following is the ac code of this problem

#include<stdio.h>
#include<iostream>
#include<queue>
using namespace std;
char mp[210][210];
int v[210][210];
int xr,yr,xa,ya;
    int n,m;
int Dx[4]={0,1,0,-1};
int Dy[4]={1,0,-1,0};
struct point{
    int x;
    int y;
    int step;
    int flag;
    point(int a,int b,int c,int d):x(a),y(b),step(c),flag(d){}
    point(){}
};
struct point u,p;
int Bfs()
{
    queue<point> r;
    r.push(point(xr,yr,0,0));
    while(!r.empty())
    {
        u=r.front();
        r.pop();
        if(u.flag==1)
        {
            r.push(point(u.x,u.y,u.step+1,0));
            continue;
        }
        if(mp[u.x][u.y]=='a')
        {
            return u.step;
        }

        for(int i=0;i<4;i++)
        {
            p.x=u.x+Dx[i];
            p.y=u.y+Dy[i];

            if(p.x>=0&&p.x<n&&p.y>=0&&p.y<m&&v[p.x][p.y]==0)
            {
                if(mp[p.x][p.y]=='@'||mp[p.x][p.y]=='a')
                {
                    r.push(point(p.x,p.y,u.step+1,0));
                }
                if(mp[p.x][p.y]=='x')
                {
                    r.push(point(p.x,p.y,u.step+1,1));
                }
                v[p.x][p.y]=1;
            }
        }
    }
    return 0;
}
int main()
{
    int t;

    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        for(int i=0;i<n;i++)
        {
            scanf("%s",mp[i]);
        }

        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                v[i][j]=0;
                if(mp[i][j]=='r')
                {
                    xr=i;
                    yr=j;
                    v[i][j]=1;
                }
            }
        }
        int ans=Bfs();
        if(ans==0)
            printf("Impossible\n");
        else{
            printf("%d\n",ans);
        }
    }
    return 0;
}

II

Bailian 4115 Naruto and Sasuke( OpenJudge - 4115: Naruto and Sasuke)

First list a diagram to briefly explain the difference from the previous question

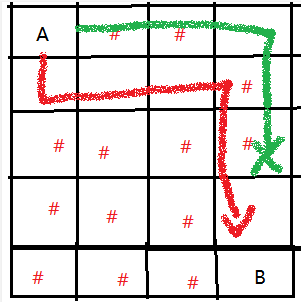
If the number of chakras is 3, if this problem does not repeatedly kill snakes killed by other paths, some situations will not be solved, so the difference between this problem and the previous problem is to repeat the path taken by other paths. If you understand this, you can use a three-dimensional array to record whether the records are accessed, not only the coordinates, but also the current number of chakras. Only when the number of chakras is the same and the current point has been accessed, you don't need to repeat the access (because the same chakras means that the number of snakes killed is the same, and being accessed means that there is a better way than the current one)

After understanding these problems, the problem is basically solved. The ac code is released below

#include<iostream>
#include<queue>
using namespace std;
char mp[210][210];
int v[210][210][20];
int Dx[4]={0,1,0,-1};
int Dy[4]={1,0,-1,0};
int m,n,k;
int xr,yr,xe,ye;
struct point{
    int x,y,t,k;
    point(int a,int b,int c,int d):x(a),y(b),t(c),k(d){}
    point(){}
};
queue<point> q;
struct point u;
int bfs()
{
    v[xr][yr][k]=1;
    q.push(point(xr,yr,0,k));
    while(!q.empty())
    {
        u=q.front();
        q.pop();
        if(u.x==xe&&u.y==ye)
            return u.t;
        for(int i=0;i<4;i++)
        {
            int nx=u.x+Dx[i];
            int ny=u.y+Dy[i];
            if(nx<0||ny<0||nx>=m||ny>=n)
                continue;
            if(mp[nx][ny]=='#'& & v [NX] [NY] [u.k-1] = = 0 & & U.K > 0) / / when you encounter an enemy and the number of remaining enemies is the same, the current path is the shortest
            {
                v[nx][ny][u.k-1]=1;
                q.push(point(nx,ny,u.t+1,u.k-1));
            }
            else if(mp[nx][ny]!='#'&&v [NX] [NY] [U.k] = = 0) / / when the number of k before clicking is the same, if you have walked the shortest way first, there is no need to go
            {
                v[nx][ny][u.k]=1;
                q.push(point(nx,ny,u.t+1,u.k));
            }
        }
    }
    return 0;
}
int main()
{
    while(cin>>m>>n>>k)
    {
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
            {
                char c;
                cin>>c;
                mp[i][j]=c;
                if(c=='@')
                {
                    xr=i;
                    yr=j;
                }
                if(c=='+')
                {
                    xe=i;
                    ye=j;
                }
            }
        int ans=bfs();
        if(ans)
            printf("%d\n",ans);
        else
            printf("-1\n");

    }

    return 0;
}

III

Bailian 4130 Saving Tang Monk( OpenJudge - 4130:Saving Tang Monk)

This question is very similar to the previous one. The function of the key in this question is equivalent to chakra, but there is one more step to find the key than the previous one. The key can only find the key 1 larger than the currently obtained key number. Another is to repeatedly visit the key room, such as key 2, Then you can't continue to access the key 2 room accessed by other paths, because the other path must be shorter than the current path (because you find the key 2 first). Therefore, the processing here is the same as the previous problem. A three-dimensional array is used to record coordinates and key numbers. But the difficulty of this problem is that when looking for the key, the same path can go back and forth, because the key is found in order. At this time, how to deal with killing the snake. For example, if you need to kill a snake to get the key 1 and then come back to get the key 2 on the current path, you need to pass through the same room with a snake twice. At this time, you need to use the three-dimensional array of keys and the state of the snake at the same time to mark the state of the Sebastes snake on a path. Here, state compression is used to represent each snake with a binary number, as shown in the following code

if(isalpha(mp[nx][ny]))
{
    bool killed=(1<<(mp[nx][ny]-'A'))&snack;
    int ns=snack+(1<<(mp[nx][ny]-'A'));
	if(killed&&!v[nx][ny][key]) {
        Q.push(point(nx,ny,time+1,key,snack));
        v[nx][ny][key]=1;
    }
    else if(!killed&&!v[nx][ny][key]) {
        v[nx][ny][key]=1;
        Q.push(point(nx,ny,time+2,key,ns));
    }
}

For ex amp le, when the snake at the next point is not killed, set the current snake (assuming that it is the first snake encountered) (using int ns = snap + (1 < < (MP [NX] [NY] - [a ')) 0001, the second snake 0011, and so on, and then use the snake number to & calculate whether it is killed. Of course, when the key is the same and the snake has been killed on another path, there is no need to repeat the current path (because the other path must be shorter). The ac code is given below( Refer to this blog )Thank you

#include<iostream>
#include<cstdio>
#include<queue>
#include<string.h>
using namespace std;
int n,k;
int xk,yk,xt,yt;
char mp[110][110];
int v[110][100][10];
int Dx[4]={0,1,0,-1};
int Dy[4]={1,0,-1,0};
struct point{
    int x,y,time,key,snack;
    point(int a,int b,int c,int d,int e):x(a),y(b),time(c),key(d),snack(e){}
    bool operator < (const point& p) const{
        return time>p.time;
    }
};
int bfs(int xk,int yk)
{
    priority_queue <point> Q;
    Q.push(point(xk,yk,0,0,0));
    v[xk][yk][0]=1;
    while(!Q.empty())
    {
        int x=Q.top().x, y=Q.top().y, time=Q.top().time, key=Q.top().key,snack=Q.top().snack;
        Q.pop();
        if(key==k&&x==xt&&y==yt)
            return time;
        for(int i=0;i<4;i++)
        {
            int nx=x+Dx[i];
            int ny=y+Dy[i];
            if(nx<0||ny<0||nx>=n||ny>=n||mp[nx][ny]=='#')
                continue;
            if(isalpha(mp[nx][ny]))
            {
                bool killed=(1<<(mp[nx][ny]-'A'))&snack;
				int ns=snack+(1<<(mp[nx][ny]-'A'));
				if(killed&&!v[nx][ny][key]) {
					Q.push(point(nx,ny,time+1,key,snack));
					v[nx][ny][key]=1;
				}
				else if(!killed&&!v[nx][ny][key]) {
					v[nx][ny][key]=1;
					Q.push(point(nx,ny,time+2,key,ns));
				}
            }
            else
            {
                if(v[nx][ny][key]==0)
                {
                    v[nx][ny][key]=1;
                    Q.push(point(nx,ny,time+1,key,snack));
                }
                if(isdigit(mp[nx][ny]))
                {
                    int nkey = mp[nx][ny]-'0';
                    if(nkey==key+1&&v[nx][ny][nkey]==0)
                    {
                        Q.push(point(nx,ny,time+1,nkey,snack));
                        v[nx][ny][nkey]=1;
                    }
                }
            }
        }
    }
    return -1;
}
int main()
{
    while(cin>>n>>k)
    {
        if(n==0)
            break;
        int snake=0;
        for(int i=0;i<n;i++)
        {
            scanf("%s",mp[i]);
        }
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            {
                if(mp[i][j]=='K')
                {
                    mp[i][j]='.';
                    xk=i;
                    yk=j;
                }else if(mp[i][j]=='T')
                {
                    mp[i][j]='.';
                    xt=i;
                    yt=j;
                }else if(mp[i][j]=='S')
                {
                    mp[i][j]='A'+snake++;
                }
            }
        memset(v,0,sizeof(v));
        int ans=bfs(xk,yk);
		if(ans==-1) cout<<"impossible"<<endl;
		else cout<<ans<<endl;
    }
    return 0;
}