This is the sorting algorithm I learned in the video of the latest left God data structure algorithm on station b 2021. I feel very good

Here to share with you

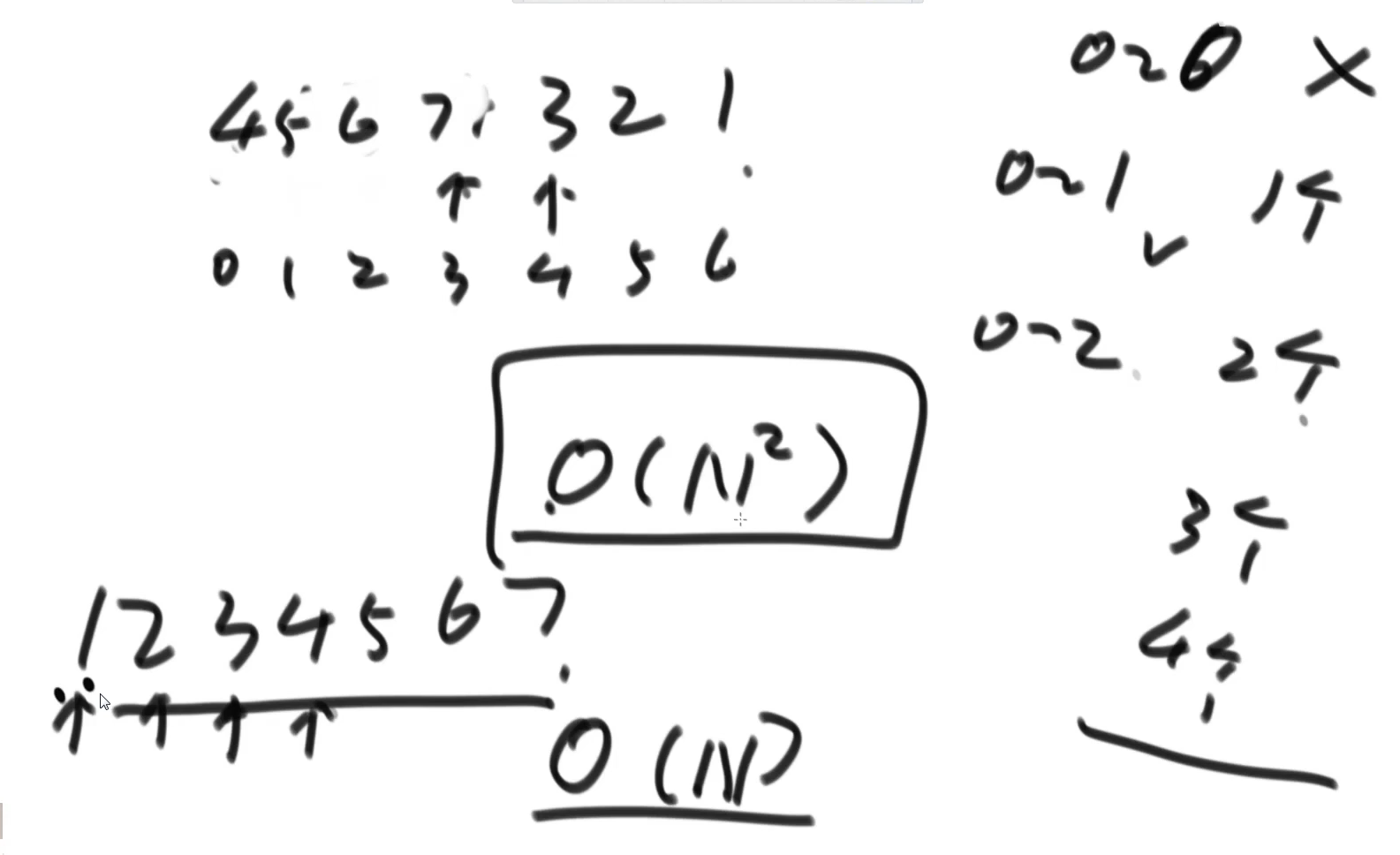
1. Select Sorting

1.1 idea of selecting sorting

Refer to the figure drawn by Zuo Shen:

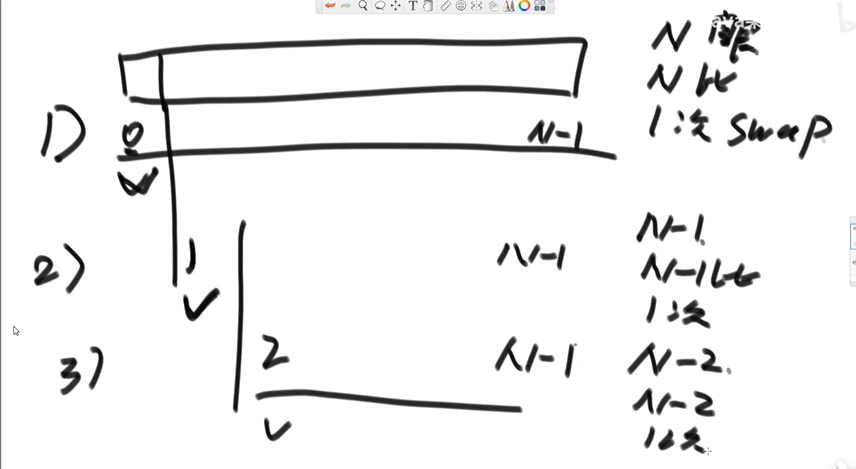
(1) Traverse the array from the beginning (subscript 0 position), find the minimum value, and exchange data with the subscript 0 position. At this time, the data at 0 position is fixed as the minimum value

(2) Starting from the subscript 1 position (the 0 position has been fixed, so it doesn't need to be considered), traverse the array again, find the minimum value, and exchange data with the subscript 1 position. At this time, the data at position 1 is also fixed

(3) Starting from the subscript 2 position (the 0 and 1 positions are fixed), traverse the array again, find the minimum value, and exchange data with the subscript 2 position. At this time, the data at position 2 is fixed

This loop continues until the last value, and the sorting is completed

1.2 time complexity

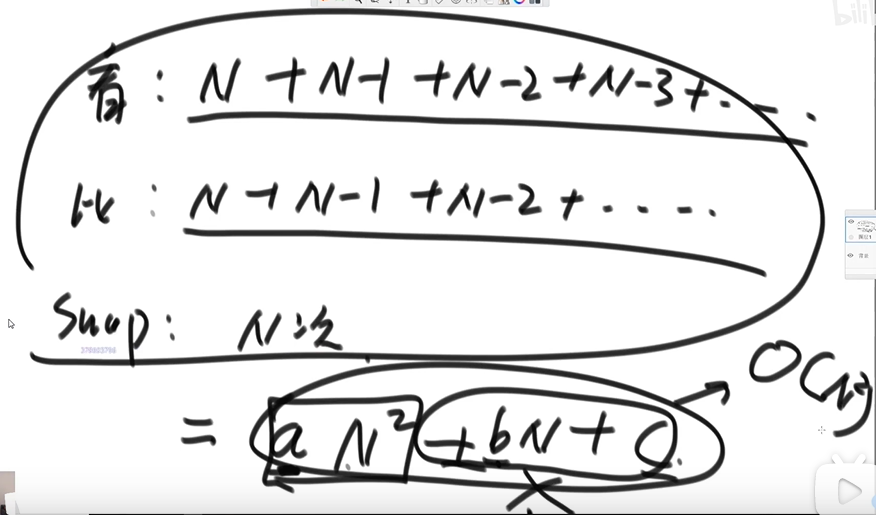
Time complexity is O(N^2)

It can be seen that the number of constant operations is an equal difference sequence ﹐ aN^2 + bN +C ﹐ we only consider that the highest term is N^2

If an operation has nothing to do with the data volume of the sample, it is completed within a fixed time every time, which is called constant operation.
 

Space complexity: additional space opened up by O(1): number I, J, variable minIndex (released every cycle)

1.3 code implementation

Left God's code:

public static void selectionSort(int arr[]){
        //If the array is empty or the array length is less than 2, it does not need to be sorted and returned directly
        if(arr == null || arr.length < 2){
            return;
        }
        //If the array length is greater than or equal to 2, sorting begins
        for (int i = 0; i < arr.length -1; i++){  // Reassign the array from i ~ N-1 in turn
            int minIndex = i; //Let's assume the minimum at position i
            for (int j = i + 1; j < arr.length; j++){  // Find the subscript of the minimum value from i ~ N-1
                minIndex = arr[j] < arr[minIndex] ? j : minIndex;
            }
            // If i and the minimum subscript are exchanged, then the i position is the minimum value. At this time, i is fixed and i + + continues from the next position
            swap(arr, i, minIndex);
        }
    }
    //Exchange data
    public  static void swap(int[] arr, int i, int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

Code idea:

Select sort from front to back

(1) Let's assume the minimum at ， i ， and assign it to minIndex

(2) [inner loop] find the minimum value from (i ~ N-1), compare this value with the current minIndex, if it is small, reassign this value to minIndex, if it is large, it will not move, and then find the next value until N-1

(3) [outer loop] the inner loop determines a minimum value once, and this value will not be considered next time, so i++

2. Bubble sorting

2.1 bubble sorting idea

Still look at the picture painted by Zuo Shen:

(1) The value of the array is above the horizontal line and the index is below the horizontal line

(2) Starting from index 0, compare the two data in turn until the last data. If the previous position is smaller than the latter position, it will not move, and if it is larger, it will be exchanged. After the comparison of the whole array, the value of the last position is the largest. At this time, the value of the last position index is fixed

(3) Start from index 0 again and compare the data in pairs until the penultimate data. After the comparison again, the value of the penultimate index is also fixed

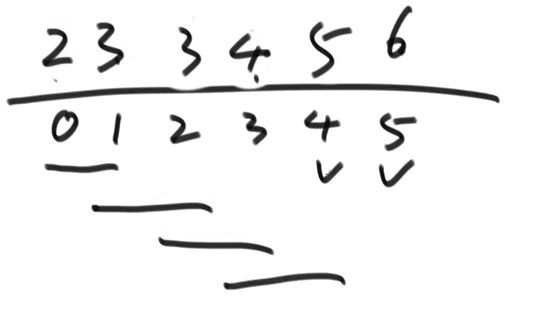
(4) cycle until the value of index position 1 is fixed, and the sorting is completed

2.2 time complexity

Time complexity is O(N^2)

It can be seen that the number of constant operations is an equal difference sequence ﹐ aN^2 + bN +C ﹐ we only consider that the highest term is N^2

2.3 code implementation

Left God's code:

public static void bubbleSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        for(int end = arr.length - 1; end > 0; end--){ // Sort from 0 to end, and fix the last position each time, end--
            for(int i = 0; i < end; i++){ //Make pairwise comparison from 0 to end each time
                if (arr[i] > arr[i + 1]){ //If the previous position is larger than the latter position, it is exchanged
                    swap(arr, i, i+1);
                }
            }
        }
    }
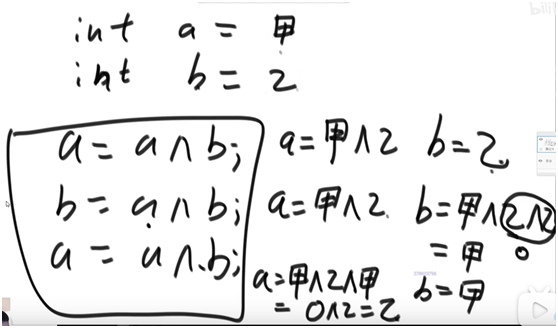
    //Exchange the values at i and j positions of arr, using XOR mechanism
    public static void swap(int[] arr, int i, int j){
        arr[i] = arr[i] ^ arr [j];
        arr[j] = arr[i] ^ arr [j];
        arr[i] = arr[i] ^ arr [j];
    }

Code idea:

Bubble sorting is sorting from back to front

(1) First initialize an end to point to the last data, and save the data with the largest value in the array

(2) [inner layer cycle] find the maximum value and compare it from (0~end). If the former position is larger than the latter position, it will be exchanged. After a cycle, the end index will save the maximum value

(3) [outer loop] a maximum value is determined when the inner loop is carried out once. At this time, this value does not need to be considered, so it is given to end--

2.4 exchanging arrays using XOR mechanism

The XOR mechanism is used to exchange array positions (super smart):

Illustration of Zuo Shenhua:

3. Insert sort

3.1 insert sorting idea

(1) First, the 0 ~ 0 range is orderly, and naturally

(2) To achieve order in the range of 0 ~ 1, the pointer points to index 1, and the data values are compared with the previous values in turn. If they are large, they will not move, and if they are small, they will be exchanged. When they are larger than the previous values or there is no data in front, they will stop. After the comparison, the range of 0 ~ 1 will be orderly

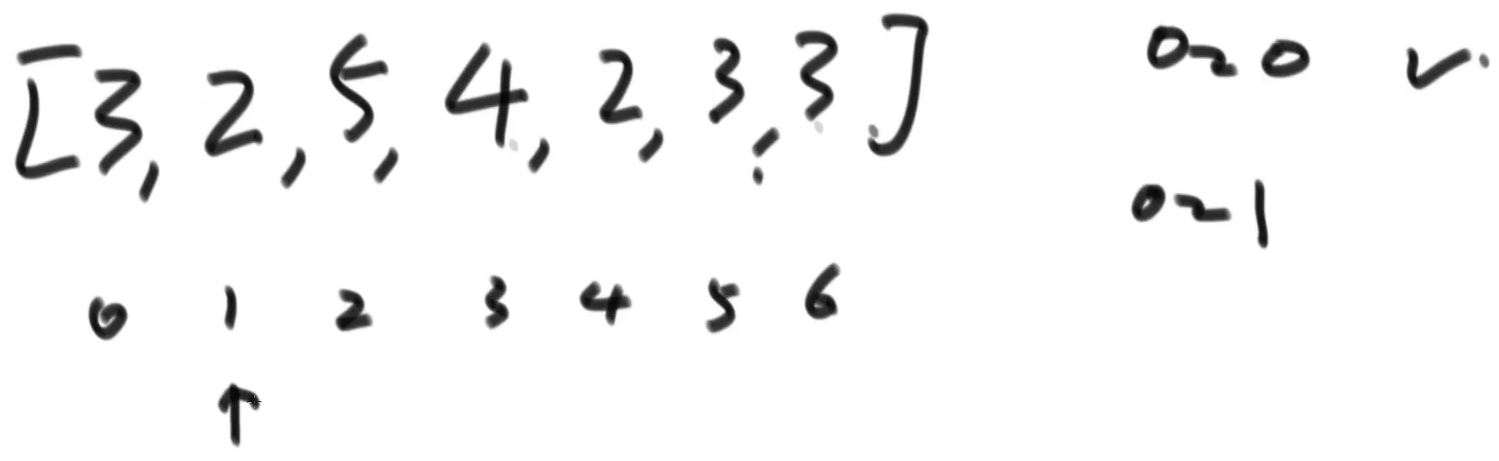
After exchange:

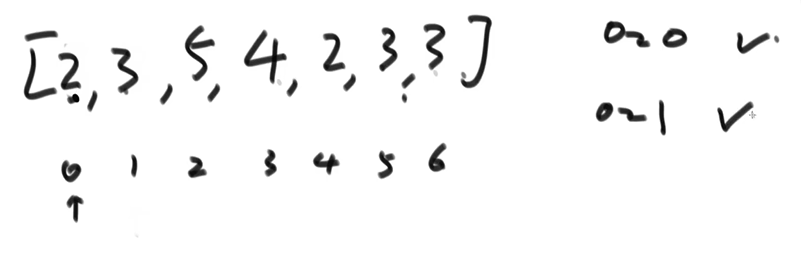
(3) To achieve order in the range of 0 ~ 2, the pointer points to index 2, and the data values are compared with the previous values in turn. If they are large, they will not move, and if they are small, they will be exchanged. When they are larger than the previous values or there is no data in front, they will stop. After the comparison, the range of 0 ~ 2 will be orderly

(4) To achieve order in the range of 0 ~ 3, the pointer points to index 3, and the data values are compared with the previous values in turn. If they are large, they will not move, and if they are small, they will be exchanged. When they are larger than the previous values or there is no data in front, they will stop. After the comparison, the range of 0 ~ 3 will be orderly

After exchange:

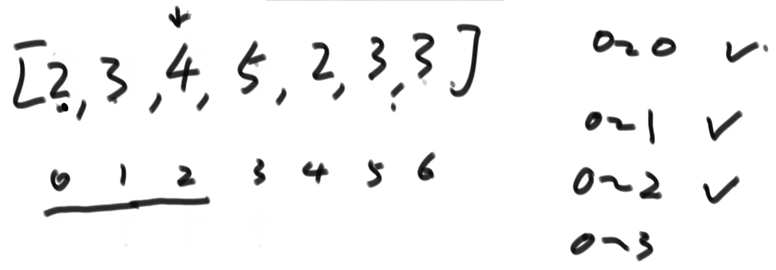
(5) repeat the cycle until the last number is also compared and stopped. At this time, the range of 0~n is orderly and the sorting is completed

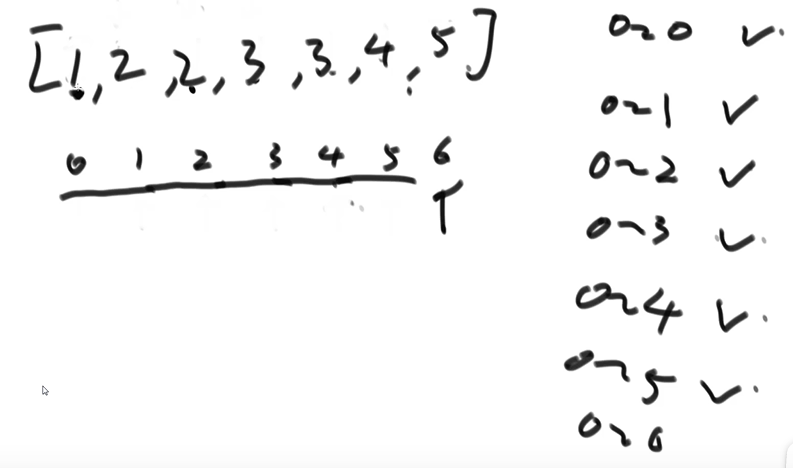
Zuo Shen's abstract understanding: playing cards

A deck of cards is arranged in ascending order from left to right. If a new card is caught, slide from right to left. If the card surface in front of it is smaller than it, insert it, and then grab the next card to continue

3.2 time complexity

Time complexity is O(N^2)

It can be seen that the number of constant operations is an equal difference sequence ﹐ aN^2 + bN +C ﹐ we only consider that the highest term is N^2

3.3 code implementation

public static void insertSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        //0 ~ 0 is naturally ordered
        //0 ~ 1 want to order
        for (int i = 1; i < arr.length; i++){
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--){
                swap(arr, j, j + 1);
            }
        }
        //Exchange data
        public static void swap(int[] arr, int i, int j){
            int tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
        }
    }

Left God diagram two-layer cycle:

If you judge the data at position 0~i, then the data within the range (0~i-1) is the previously arranged data, and I is equivalent to the new number

Let J take the number on i-1, then the current number i is in the position of j+1. At this time, it is compared. If [J] > [j+1], it is exchanged

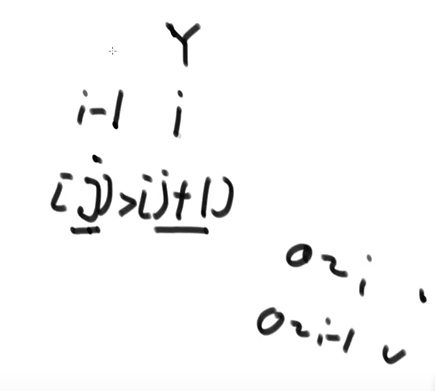
At this time, the current number i is switched to the i-1 position. If J -- is given, then J takes the number on i-2, and at this time, the current number i is still in the j+1 position (in fact, the current number is always in the j+1 position). If [J] > [j+1], the current number i is switched until the current number i is greater than the previous number or i stops the cycle at the index 0 position. At this time, the range of 0~i is in order

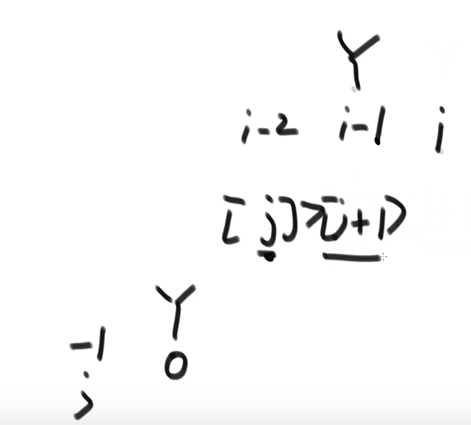
Put the picture first (KDA kasha Zhizhen 2018)