Based on Weka platform, the attribute weighted naive Bayesian algorithm based on differential evolution algorithm is studied
Personal interest, hope to help you
preface
naive Bayesian algorithm is widely used because of its high classification accuracy and simple model, but it is difficult to realize in practical classification learning because it needs to have strong conditional independence assumption between attributes. To solve this problem, a weighted naive Bayesian classification algorithm (DE_AWNB) based on differential evolution algorithm is proposed. The algorithm combines the differential evolution algorithm (DE) with the attribute weighted naive Bayesian algorithm, generates the initial population in a random way, takes the classification accuracy as the fitness function, and carries out generation by generation optimization. Finally, a set of weights with the highest fitness function value in the total iterative process are applied to the attribute weighting to construct a naive Bayesian classifier. Experiments show that the classification ability of attribute weighted naive Bayes based on differential evolution algorithm is slightly higher than that of naive Bayes classifier.
1, Introduction
among various classification algorithms in pattern recognition, naive Bayesian algorithm is widely used because of its simple model, high efficiency and high accuracy. However, because the conditional independence assumption of naive Bayes is difficult to meet in practical application, many scholars improve its performance by studying and learning Bayesian networks. Foreign scholar Zhang Harry proposed five Weighted Naive Bayes (WNB) algorithms to evaluate the impact of each class attribute on classification in different directions and give different weights to class attributes. This algorithm not only retains the advantages of high classification accuracy of naive Bayes, but also weakens the assumption of conditional independence of class attributes, The performance of naive Bayesian algorithm is optimized to a certain extent. Experiments show that the weight solution combined with mountain climbing method and Monte Carlo improves the performance of classifier to a great extent.
in fact, according to experience, solving the optimal attribute weight based on evolutionary algorithm is an effective and feasible way in theory. Therefore, in this paper, I will study the attribute weighted naive Bayesian classifier based on differential evolution algorithm. My general idea is to take the n-dimensional vector composed of N attribute weights (range 0-1) as individuals, randomly generate 100 individuals to form the initial population, take the accuracy of classification as the fitness function, use the differential evolution algorithm to iterate continuously, and finally take the individual with the highest fitness function in the offspring as the optimal weight to improve the accuracy of the model. The experiment is carried out by using the data set of weka platform.
2, Theoretical model and construction ideas
1. Differential evolution algorithm
differential evolution algorithm is a kind of evolutionary algorithm. It is a kind of random optimization algorithm based on population. It mainly adopts real number coding to solve real number optimization problems. The main operator of the differential evolution algorithm is the differential mutation operator. The operator uses the difference information between different individuals and has adaptability in search direction and search step. The two individual vectors in the same population are differentiated and scaled, and added with the third individual vector in the population to obtain a mutation individual vector; Then the fitness of the mutated individual vector is compared with the parent individual vector, and the better one is saved in the next generation population. In this way, the differential evolution algorithm uses operators such as differential mutation, hybridization and selection to evolve the population until it reaches the termination condition and exits. The algorithm has the advantages of simple structure, easy to use, fast convergence and strong robustness. These advantages make the algorithm widely used, such as pattern recognition, data mining and so on.
2. Naive Bayesian classification algorithm

(the above picture is compiled by me with reference to watermelon book. Since the formula is not easy to edit, I will directly present a screenshot to you)
3, Attribute weighting algorithm based on differential evolution algorithm
1. Attribute weighted naive Bayes
due to the practical application of the assumption of naive Bayesian conditional independence, in order to weaken the influence of its assumption of attribute conditional independence, some scholars give corresponding weights to attributes according to the importance of attributes to classification, and propose attribute weighted naive Bayesian model (AWNB):

2. Attribute weighted naive Bayesian algorithm based on differential evolution algorithm
the improved weighted naive Bayes classifier AWNB relaxes the conditional independence assumption of naive Bayes and is satisfied in practical application. Attribute weighting algorithm performs well on some data sets, but it does not perform well on other data sets. At present, scholar J Liu combines hybrid simulated annealing and genetic algorithm to optimize the attribute set, and proposes a naive Bayesian algorithm based on evolutionary algorithm. Many scholars combine evolutionary algorithm with Bayesian algorithm and achieve good results. Therefore, we propose a weighted naive Bayesian classification algorithm based on differential evolution algorithm.
2.2.1 coding method
in the way of real number coding, each chromosome is composed of a group of real numbers. The weight of the corresponding attribute of each chromosome is the number of attributes in the data set, and each real number bit corresponds to the weight of each attribute in turn.
2.2.2 initial population
search with random numbers between 0 and 1 as the initial population. The advantage of this method is that the diversity of the population is relatively strong to prevent falling into local optimization.
2.2.3 fitness function
the fitness function is the classification accuracy of Bayesian classifier, which is reflected in the program as the function public double performance (instances, double[] weight), where instances refers to the instance of the test set, and weight refers to one of our individuals (chromosomes), that is, the attribute weight value. The function predicts the class tags of all instances and returns the correct rate.
2.2.4 algorithm parameter setting
the parameters of differential evolution algorithm include population size, maximum algebra of algorithm execution, crossover probability, scaling factor, etc. The parameters used are as follows: population size NP=50, maximum algebraic generation=100, crossover probability CR=0.7, scaling factor F changes adaptively with the algebra of the algorithm, and the adaptive operator changes exponentially, so that F decreases from 0.7 to 0.35 to prevent premature.
2.2.5 algorithm prototype
referring to the prototype of attribute selection algorithm based on evolutionary algorithm given by Jiang, this paper obtains the attribute weighting algorithm based on differential evolutionary algorithm as shown in table 2.2.

3. Experimental results
the proposed attribute weighted naive Bayes classifier based on differential evolution algorithm is applied to six Weka's own data sets to verify its improvement effect in Weka platform. The six data sets are as follows: breast cancer, contact lens, vote, weather and label. The numerical attributes are discretized by the tutor filter Discretize in Weka platform. The training set accounts for 66% and the test set accounts for 34%.
using the naive Bayesian classifier based on the attribute weighting of differential evolution algorithm, we conducted five experiments on each data set (the screenshot of the operation results of weka platform is shown in the appendix; in fact, in order to ensure the accuracy of the experiment, dozens of experiments should be conducted to avoid the contingency of the results; here, only five times are recorded for the convenience of displaying the data). Record the classification accuracy and calculate the average value, as well as the results obtained by weka's own naive Bayesian classifier, as shown in Table 3.1:
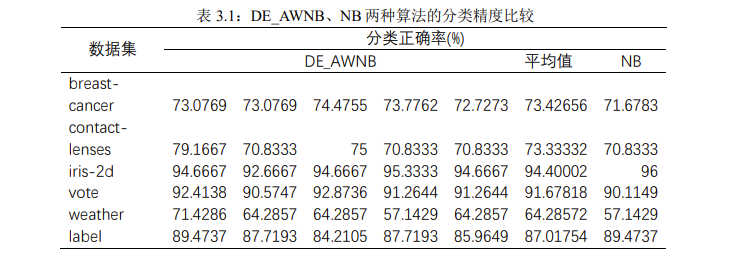
in order to intuitively show the classification ability of naive Bayes classifier and naive Bayes classifier based on attribute weighting of differential evolution algorithm, we compare the classification accuracy of the two classifiers on each data set, as shown in Figure 3.1:
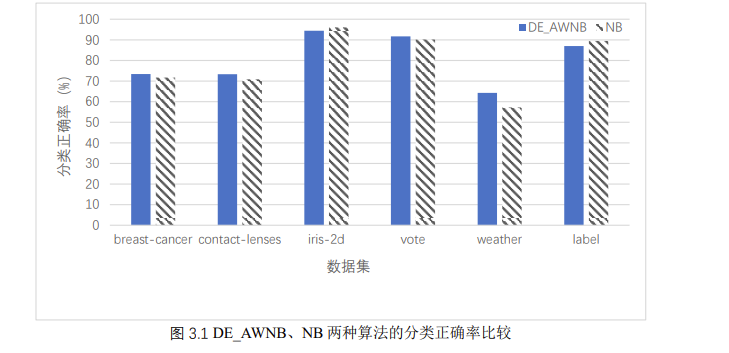
as can be seen from the above figure, De_ The classification ability of awnb is only slightly higher than that of NB, in which the classification accuracy of the four data sets of blast cancer, contact lens, vote and weather is higher than that of NB, and lower than that of NB in iris-2d and label data sets. In general, the classification ability of naive Bayes classifier based on differential evolution algorithm is slightly better than naive Bayes.
appendix
The code is as follows:
package weka.classifiers.mfh;
import weka.core.*;
import java.util.Iterator;
import java.util.Random;
import org.netlib.util.doubleW;
import java_cup.internal_error;
import weka.classifiers.*;
public class EAB extends AbstractClassifier {
private double [][] m_ClassAttCounts;
private double [] m_ClassCounts;
private int [] m_NumAttValues;
private int [] m_StartAttIndex;
private int m_TotalAttValues;
private int m_NumClasses;
private int m_NumAttributes;
private int m_NumInstances;
private int m_ClassIndex;
private double [][] Weights; //Weighted population matrix
public double [] fbest; //Optimal individual
private double fbest_fitness; //Optimal fitness
public int NP =50; /*Population individual quantity*/
public int generation =100;//Number of iterations
public double F=0.5;//Scaling factor
public double CR=0.5;//Crossover probability
/*Variogram, the parameter is the population composed of instance and attribute weight*/
public double[][] mutation(Instances instances,double[][] iter1) throws Exception{
double[][] v=new double[iter1.length][iter1[1].length];
/*Three different individuals are selected to construct the difference vector*/
for(int i=0;i<NP;i++) {
int r1=(int)(Math.random()*NP);
while(r1==i)
r1=(int)(Math.random()*NP);//Ensure that r1 is not the same as i
int r2=(int)(Math.random()*NP);
while(r2==r1||r2==i)
r2=(int)(Math.random()*NP);//Ensure that r2 is not the same as r1 and i
int r3=(int)(Math.random()*NP);
while(r3==r2||r3==r1||r3==i)
r3=(int)(Math.random()*NP);//Ensure that r3 is not the same as the first three vectors
/*Make the difference vector always point to the region with high fitness value*/
if(Performance(instances,iter1[r2])>Performance(instances, iter1[r3]))
//When the weight is r2, the classification accuracy is greater than that when the weight is r3
for(int j=0;j<v[1].length;j++) {
v[i][j]=iter1[r1][j] + F*(iter1[r2][j]-iter1[r3][j]);
if(v[i][j]<0)v[i][j]=Math.random();
if(v[i][j]>1)v[i][j]=Math.random();
}
else //When the weight is r3, the classification accuracy is greater than that when the weight is r2
for(int j=0;j<v[1].length;j++) {
v[i][j]=iter1[r1][j] + F*(iter1[r3][j]-iter1[r2][j]);
if(v[i][j]<0)v[i][j]=Math.random();
if(v[i][j]>1)v[i][j]=Math.random();
}
}
return v;//Returns the difference vector
}
/*Cross function, the parameters are the population and difference vector of attribute weight*/
public double[][] cross(double[][] weight,double[][] v) throws Exception{
double[][] child = new double[v.length][v[1].length];//Used to store subgroups obtained after crossing
for(int i=0;i<NP;i++) {
for(int j=0;j<v[1].length;j++) {
/*If the obtained random number is less than 0.7 or the random intersection is equal to j, the intersection is performed*/
if(Math.random()<=CR||(j==(int)(Math.random()*(v.length+1))))
child[i][j]=v[i][j];
else //Otherwise, do not cross
child[i][j]=weight[i][j];
}
}
return child;
}
/*Select the function, and the input is the subgroup, initial population and instance obtained by crossover*/
public double[][] selection(double[][] child,double[][] weight,Instances instances) throws Exception{
/*In the one-to-one tournament, individuals with high classification accuracy are added to the new population*/
for(int i=0;i<NP;i++)
if(Performance(instances,weight[i])<Performance(instances, child[i]))
weight[i]=child[i];
return weight;
}
/*Calculate the classification accuracy, input as instance and attribute weight*/
public double Performance(Instances instances,double[] weight) throws Exception
{
int realnum =0;//Used to record the number of correct classifications
for(int num=0; num < instances.numInstances();num++) {
double [] probs = new double[instances.numClasses()];
Instance ins = instances.instance(num);
probs = predict_tmp(ins,weight);//Record the probability of ins in each class
int max=0;
for(int i1=0;i1<instances.numClasses();i1++)
{
if(probs[i1]>probs[max])max=i1;//Record the most likely class
}
int real_class = (int)ins.classValue();//Read real class Tags
if(real_class==max)realnum++;//The prediction is the same as the actual, realnum++
}
return 1.0*realnum/instances.numInstances();
}
public void buildClassifier(Instances instances) throws Exception {
m_NumClasses = instances.numClasses();//Number of classes
m_ClassIndex = instances.classIndex();//Class in the array, used for positioning
m_NumAttributes = instances.numAttributes();//The number of attributes needs to be reduced by 1 when used, because it includes classes
m_NumInstances = instances.numInstances();//Number of data sets
m_TotalAttValues = 0;//Used to calculate the relative subscript of each attribute
m_StartAttIndex = new int[m_NumAttributes];//Subscript corresponding to attribute
m_NumAttValues = new int[m_NumAttributes];//Number of attribute values under attribute
/*Calculates the subscript at the beginning of each attribute*/
for(int i = 0; i < m_NumAttributes; i++) {
if(i != m_ClassIndex) {
m_StartAttIndex[i] = m_TotalAttValues;
m_NumAttValues[i] = instances.attribute(i).numValues();
m_TotalAttValues += m_NumAttValues[i];
}
else {
m_StartAttIndex[i] = -1;
m_NumAttValues[i] = m_NumClasses;
}
}
m_ClassCounts = new double[m_NumClasses];//Number of class Tags
m_ClassAttCounts = new double[m_NumClasses][10000];//Number of occurrences of each class tag
/*Count the number of times each class tag is under each attribute*/
for(int k = 0; k < m_NumInstances; k++) {
int classVal=(int)instances.instance(k).classValue();
m_ClassCounts[classVal] ++;
int[] attIndex = new int[m_NumAttributes];
for(int i = 0; i < m_NumAttributes; i++) {
if(i == m_ClassIndex){
attIndex[i] = -1;
}
else{
attIndex[i] = m_StartAttIndex[i] + (int)instances.instance(k).value(i);
m_ClassAttCounts[classVal][attIndex[i]]++;
}
}
}
/*Array, used to generate weight population*/
double[] norm_array = new double[m_NumAttributes-1];
Weights = new double[NP][m_NumAttributes-1];//Initial population
/*Construct initial population*/
for(int num=0;num< NP;num++) {
for(int num2=0;num2<m_NumAttributes-1;num2++) {
double i = Math.random();
norm_array[num2] = i;
}
for(int num3=0;num3<m_NumAttributes-1;num3++) {
Weights[num][num3] = norm_array[num3];
}
}
fbest = new double[m_NumAttributes-1];
fbest_fitness = Double.NEGATIVE_INFINITY;
int n=0;
/*The optimal solution process of differential fireworks algorithm*/
for(int i=0;i<generation;i++) {
n=1;
double [][]v =new double[NP][m_NumAttributes-1];//Used to store difference vectors
v= mutation(instances, Weights);//variation
double [][]weight = new double[NP][m_NumAttributes-1];//Used to store the population obtained after crossing
weight = cross(Weights, v);//overlapping
Weights = selection(weight, Weights, instances);//One to one tournament selection to generate new species groups
/*Calculate the best individual in the current population*/
double best_fitness=Performance(instances, Weights[0]);
double []best = Weights[0];
for(int j=1;j<NP;j++) {
if(Performance(instances, Weights[j])>best_fitness) {
best_fitness = Performance(instances, Weights[j]);
best=Weights[i];
}
}
/*If the best individual of the current population is better than the global best individual, replace it*/
if(best_fitness>fbest_fitness) {
fbest_fitness=best_fitness;
fbest=best;
}
/*Adaptive operator, using self adaptation to change the scaling factor F*/
double suanzi = Math.exp(1 - generation / (generation + 1 - n));
F = 0.35 * Math.pow(2,suanzi);
}
}
public double [] distributionForInstance(Instance instance) throws Exception {
double [] probs = new double[m_NumClasses];
int[] attIndex = new int[m_NumAttributes];
for(int att = 0; att < m_NumAttributes; att++) {
if(att == m_ClassIndex)
attIndex[att] = -1;
else
attIndex[att] = m_StartAttIndex[att] + (int)instance.value(att);
}
for(int classVal = 0; classVal < m_NumClasses; classVal++) {
/*The probability that the calculation example belongs to the current class is used, the Laplace smoothing is used, and the formula of attribute weighting is used to calculate the probability*/
probs[classVal]=(m_ClassCounts[classVal]+1.0)/(m_NumInstances+m_NumClasses);
for(int att = 0; att < m_NumAttributes; att++) {
if(attIndex[att]==-1) continue;
probs[classVal]*=Math.pow((m_ClassAttCounts[classVal][attIndex[att]]+1.0)/(m_ClassCounts[classVal]+m_NumAttValues[att]),(fbest[att]));
}
}
Utils.normalize(probs); //The probability of belonging to each class of markers will be obtained and standardized
return probs;
}
/*Calculate the class mark predicted by an instance under the current weight*/
public double [] predict_tmp(Instance instance,double[] weight) throws Exception {
double [] probs = new double[m_NumClasses];
int[] attIndex = new int[m_NumAttributes];
for(int att = 0; att < m_NumAttributes; att++) {
if(att == m_ClassIndex)
attIndex[att] = -1;
else
attIndex[att] = m_StartAttIndex[att] + (int)instance.value(att);
}
for(int classVal = 0; classVal < m_NumClasses; classVal++) {
/*Use the probability that the calculation example belongs to the current class, use Laplace smoothing, and use the formula of attribute weighting to calculate the probability,*/
probs[classVal]=(m_ClassCounts[classVal]+1.0)/(m_NumInstances+m_NumClasses);
for(int att = 0; att < m_NumAttributes; att++) {
if(attIndex[att]==-1) continue;
probs[classVal]*=Math.pow((m_ClassAttCounts[classVal][attIndex[att]]+1.0)/(m_ClassCounts[classVal]+m_NumAttValues[att]),(weight[att]));
}
}
return probs;
}
public static void main(String [] argv) {
runClassifier(new GAB(), argv);
}
}
2. Experimental screenshot

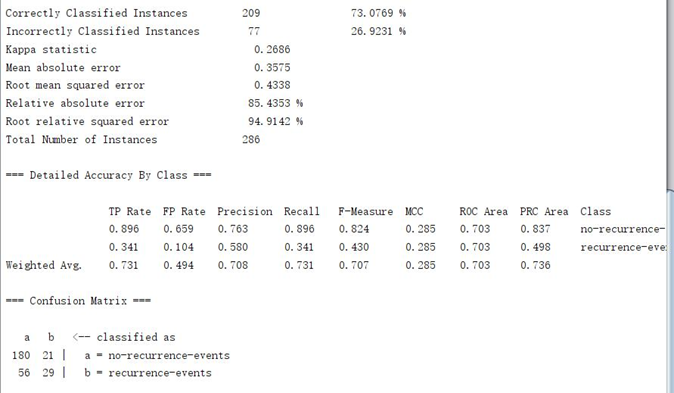
The space is too large. Only the breast cancer dataset is listed. I hope it will be helpful to you