Title Description

• You are given an integer array nums and an integer target.

• You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.

• For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".

• Return the number of different expressions that you can build, which evaluates to target.

• You are given an integer array nums and an integer number target

• Add + or - Symbols to the num array, and then link all integers to build an expression

• For example, if num is [2,1], you can add a + before 2 and a - before 1, and then connect them to form an expression "+ 2-1"

• Return all the expressions you can build, and the final result is target

Test sample

• Example 1:

  • Input: nums = [1,1,1,1,1], target = 3
  • Output: 5
    Explanation: There are 5 ways to assign symbols to make the sum of nums be target 3.
    -1 + 1 + 1 + 1 + 1 = 3
    +1 - 1 + 1 + 1 + 1 = 3
    +1 + 1 - 1 + 1 + 1 = 3
    +1 + 1 + 1 - 1 + 1 = 3
    +1 + 1 + 1 + 1 - 1 = 3

• Example 2:

  • Input: nums = [1], target = 1
  • Output: 1

• Constraints:

  • 1 <= nums.length <= 20
  • 0 <= nums[i] <= 1000
  • 0 <= sum(nums[i]) <= 1000
  • -1000 <= target <= 1000

Violent recursive implementation

Train of thought analysis

• The simple point is to put + and - symbols before each number, traverse all cases, and count the qualified allocated quantity.
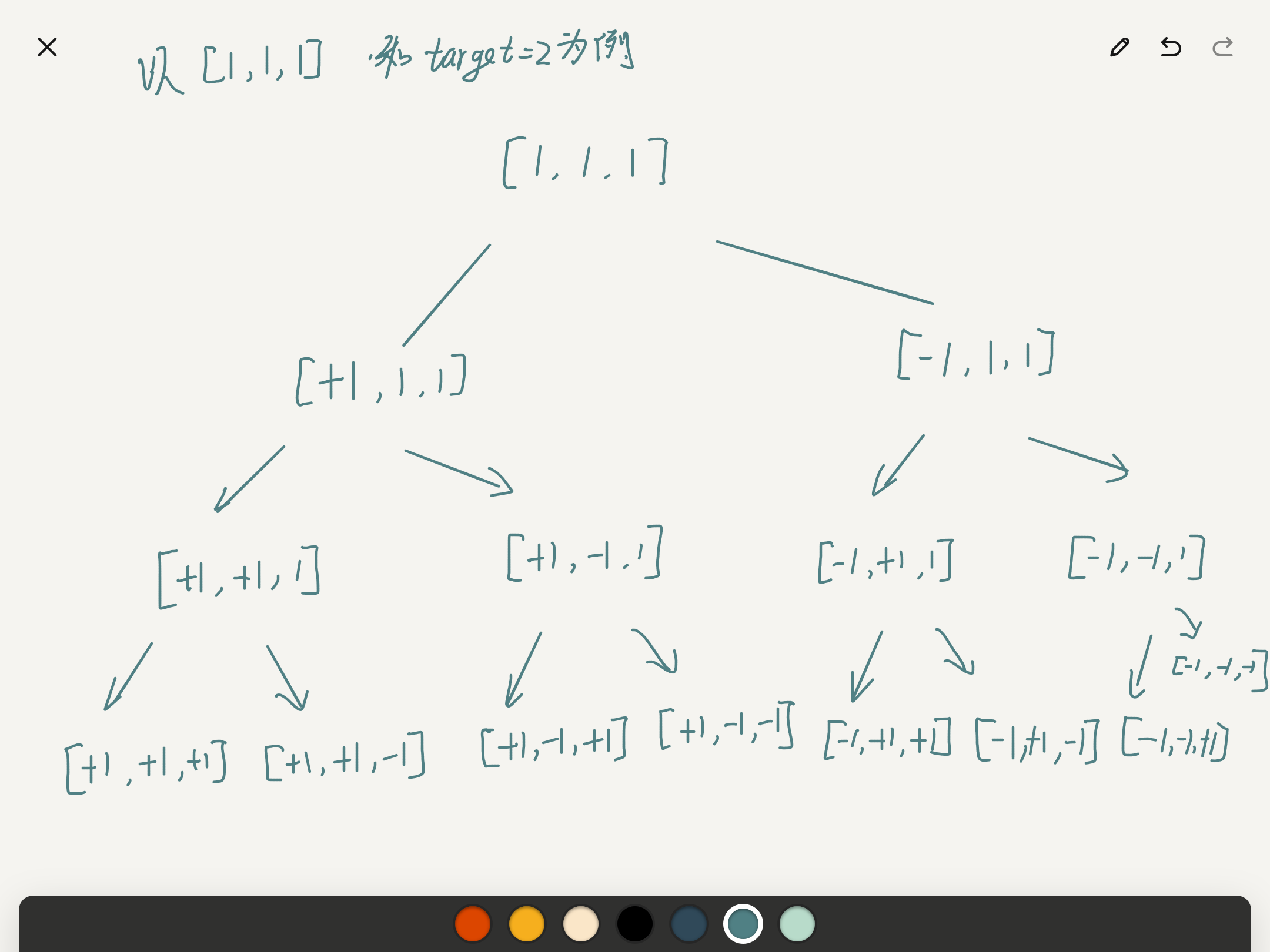
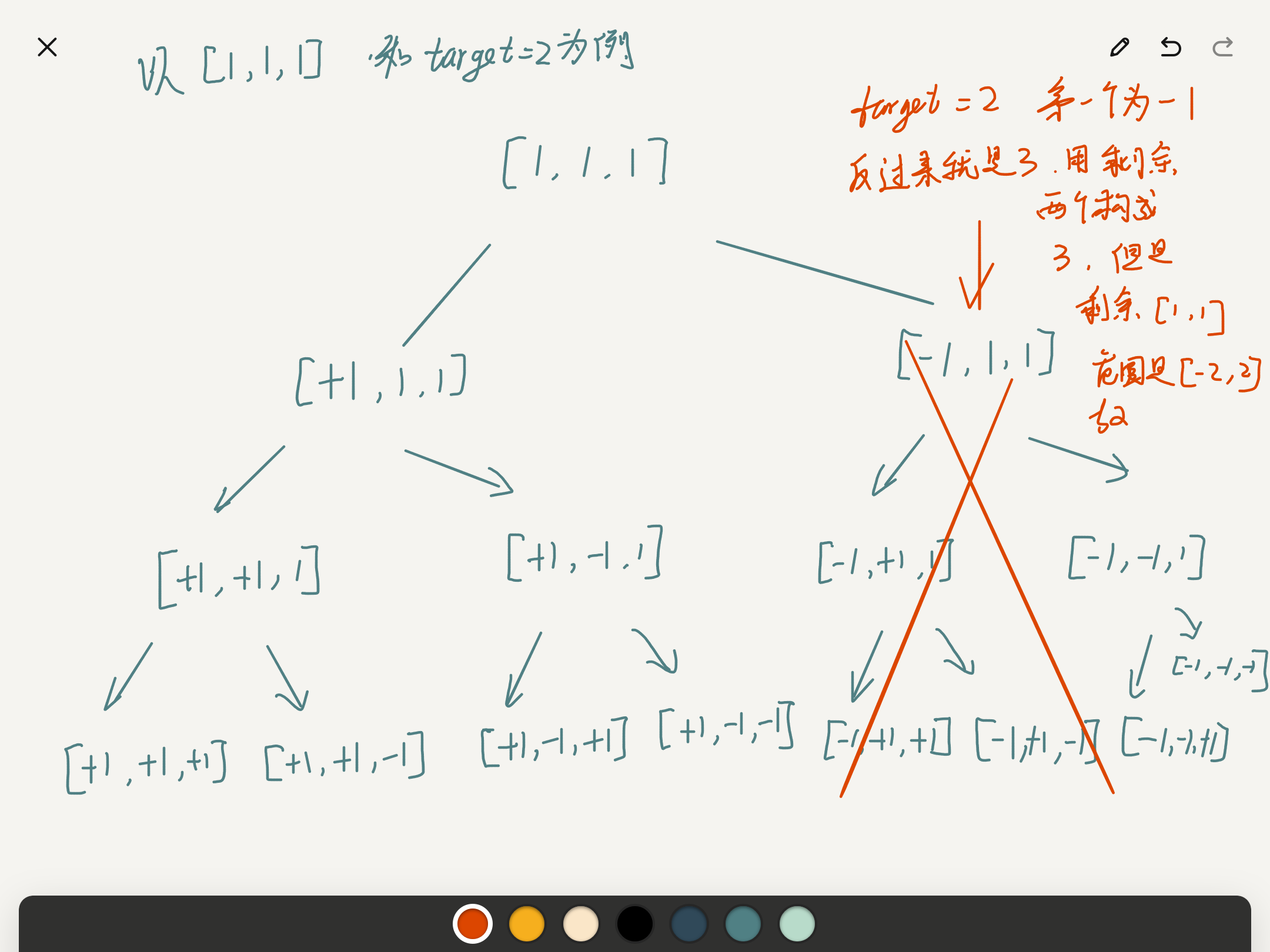
• Similar to the tree structure, direct backtracking implementation is OK.
• Pruning strategy: calculate the current residual value, the range of the number of remaining elements that can be formed, and whether to include it.
  

Implementation source code

Submission process

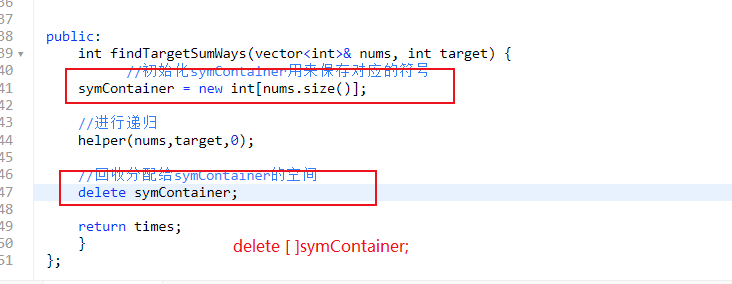
First submission of alloc and mismatch

• Note that new and delete must be used together here. If you want to clear all the array space you apply for, you must add the name of the delete [] pointer

Second submission - time limit exceeded

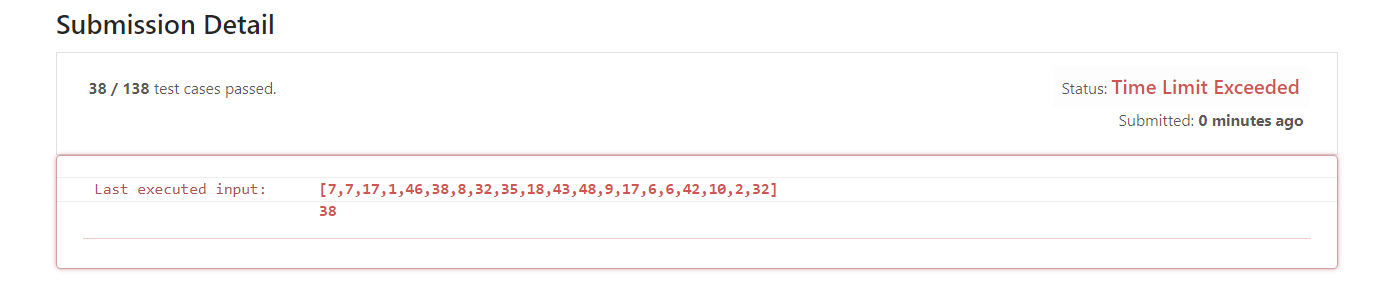
• Last executed input:
  • [20,48,33,16,19,44,14,31,42,34,38,32,27,7,22,22,48,18,48,39]
  • [20,48,33,16,19,44,14,31,42,34,38,32,27,7,22,22,48,18,48,39]
• It is explained here that the time limit is exceeded, so how to optimize? Add pruning so that it does not continue to traverse down. What should I do? At least you know the minimum and maximum values of all subsequent numbers. You can determine the minimum and maximum values when you compare them. If you have exceeded the final result, you can exit directly. The idea of branch and bound is introduced here to increase the strength of pruning.

Third submission

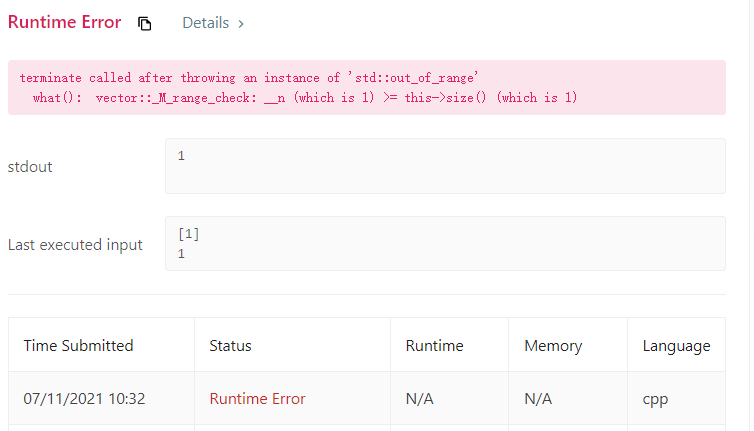
• The difficult example above has been tried, but for a special example that fails, test it locally
• The array is out of bounds. I wrote it in the wrong place
  

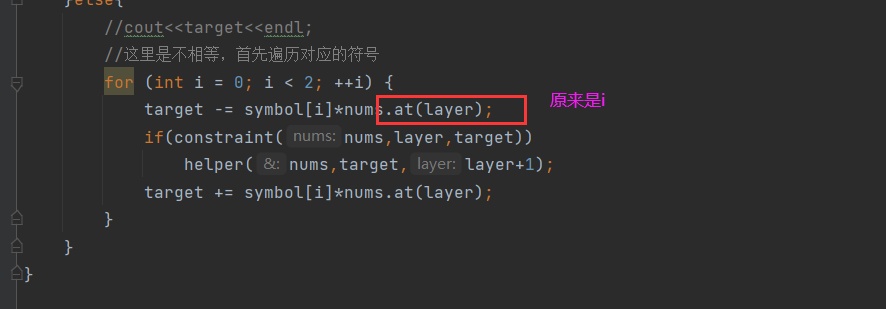
Fourth submission

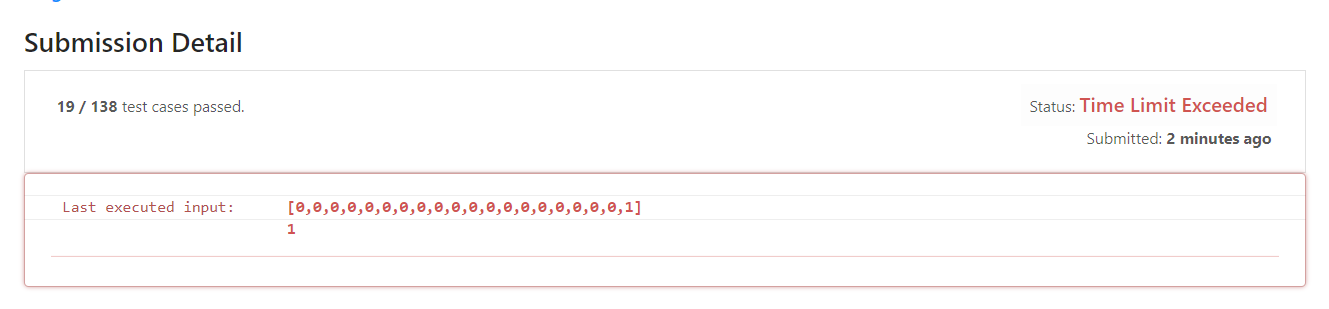
• Again, the time has exceeded the scheduled deadline. What's going on?

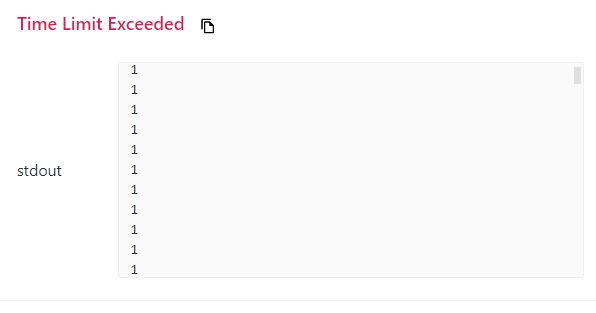
• It turned out that an output statement was not deleted.

Fifth submission

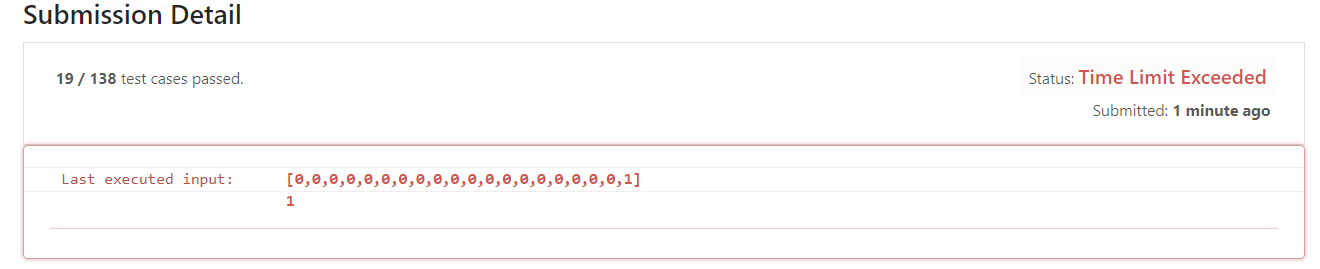
• There are still problems, which means that this place really needs pruning, otherwise it can't pass.
• Strategy:
  • Reduce loops as much as possible and integrate all loops into the overall traversal and recursion process
• After modification

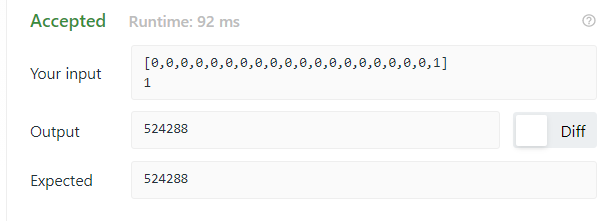
Sixth submission

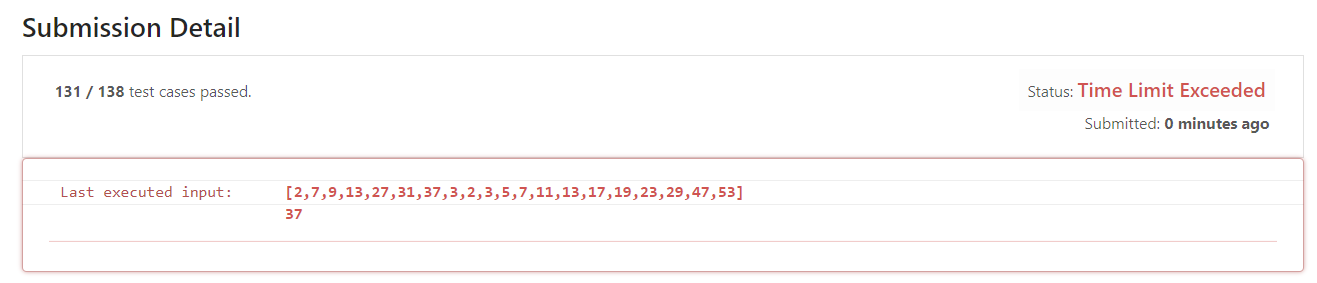
• I'm really speechless. I can't pass this. I'm still a little short. I'm still short of seven examples. How can I reduce them? I really think it has been changed to the end. This code is really concise. I'll see where it can be changed!

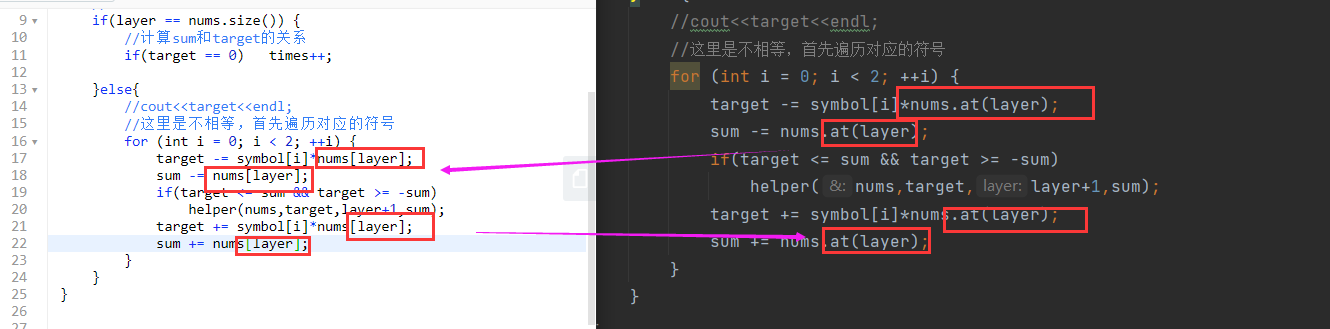
• You may not believe it. It's too late, because at takes more time than "[]" because it has an extra judgment process

Last submission

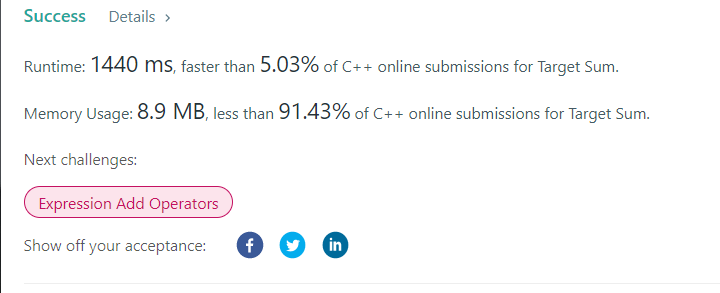
Implementation source code

#include <iostream>
#include <vector>
#include <sstream>

using namespace std;

int times = 0;
int symbol[2]={-1,1};


/*
 * Description: the backtracking part of the backtracking algorithm
 * Parameter: num is the number to be backtracked
 *      target Is the final goal to be calculated
 *      layer Is the condition for backtracking iteration
 *      sum Is the sum of the remaining items in the current sequence
 * Return: the final result is achieved by modifying the sum total
 */
void helper(vector<int> &nums,int target,int layer,int sum){

    //View conditions for recursive termination
    if(layer == nums.size()) {
        //Calculate the relationship between sum and target
        if(target == 0)   times++;

    }else{
        //cout<<target<<endl;
        //Here is inequality, first traverse the corresponding symbols
        for (int i = 0; i < 2; ++i) {
            target -= symbol[i]*nums.at(layer);
            sum -= nums.at(layer);
            if(target <= sum && target >= -sum)
                helper(nums,target,layer+1,sum);
            target += symbol[i]*nums.at(layer);
            sum += nums.at(layer);
        }
    }
}

/*
 * Description: use the addition and subtraction symbols to obtain the number of all expressions that can constitute the target
 * Parameter: nums: array of corresponding integer numbers
 *      target Is the goal that needs to be formed
 * Return: the number of target expressions whose final result is target
 * Principle: using backtracking
 */
int findTargetSumWays(vector<int>& nums, int target) {

    int sum = 0;
    for (int i = 0; i < nums.size(); ++i) {
        sum += nums.at(i);
    }

    //Recursion
    helper(nums,target,0,sum);

    return times;
}

int main() {

    //Get user input
    vector<int> nums;
    string a;
    getline(cin,a);
    int target;
    cin>>target;

    //Clear the first and second parentheses
    a = a.erase(0,1);
    a = a.erase(a.size()-1,1);

    //Split string
    stringstream sstr(a);
    string token;
    while(getline(sstr,token,',')){
        nums.push_back(atoi(token.c_str()));
    }

    //Call function direct output
    int  result;
    result = findTargetSumWays(nums,target);

    cout<<result<<endl;


    return 0;
}

Separate analysis and summary

• This topic really wastes a lot of effort, including the continuous refinement of code and many small details. Like this question, the question itself does not require you to write out all possible combinations, but allows you to output the number of combinations, so you simply need to count the number. There is no need to set an array to record the possible values* This problem needs to take a good look at what others do, because in fact, I'm a marginal ball. If I ask for a higher level, I can't pass it.

The following is the method of referring to others

Brute Force

Train of thought analysis (this part is a translation combined with my own understanding)

• The violence method is based on recursion. We need to put the + and - Symbols in front of each position of the num sequence, and then find the allocation of the final sum as S.
• For this, we use the recursive function calculate (Num, I, sum, s).
  • The return value is an expression equal to sum.
  • Principle: this function traverses forward from the ith element, and the sum of the elements before the ith element is sum. This function adds a + or - before the current index, and then updates sum + num [i] and sum num [i] according to the symbol. In addition, it also updates the index, i+1, and finally makes a self call. Whenever we reach the end of the array, we compare the obtained sum with the target value S. If they are equal, we increase the most important return count value
• Therefore, the function call calculate returns all qualified allocation formulas.
• If you don't understand, just look at the code

Implement your own source code. int count = 0;

/*
 * Description: a specific function of recursion. Through deep recursion, the relationship between the continuously adjusted value and the target value is obtained
 * Parameter: num array to be tested
 *      sum Is the number that can be combined by the numbers before the current index
 *      index Is the index currently traversed
 *      target Is the target value to be compared
 * Return: no return. Increase the statistical value by changing the corresponding count
 */
void calculate(vector<int> &nums,int sum,int index,int target){

    //Recursive termination condition
    if(index == nums.size()){
        if(sum == target)   count ++;
    }else{
        //cout<<"current sitaution is sum is"<<sum<<"index is"<<index<<endl;
        //Calculate recursion like two directions respectively
        calculate(nums,sum+nums.at(index),index+1,target);
        calculate(nums,sum-nums.at(index),index+1,target);
    }
}

int findTargetSumWays2(vector<int> &nums,int target){
    calculate(nums,0,0,target);
    return count;
}

Submission process

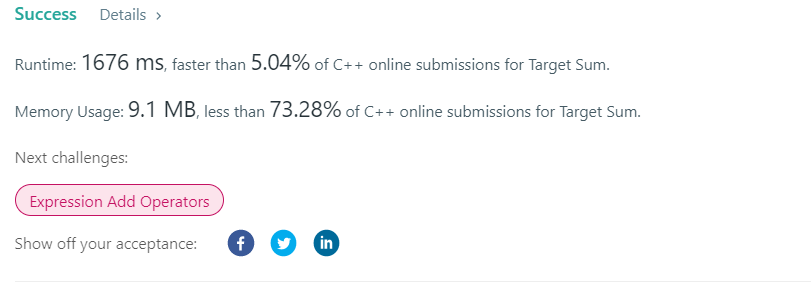
Note that when calling a function, do not write i + +, write i+1

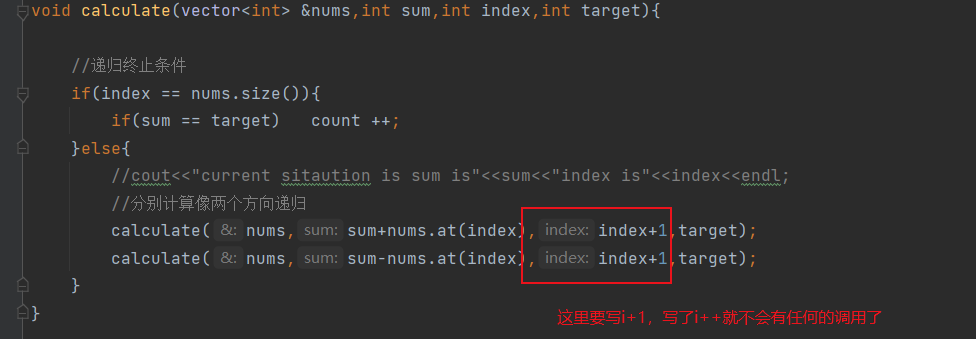
Analysis and summary

• In the case of using recursion, my time is actually slower than his. He doesn't have any pruning, which is bound to waste a lot of time. I already have a lot of pruning, which should spend less time than him in theory, but it's strange to be similar to him. It shows that I have spent a lot of calculation in the process of comparison.
• At the same time, in addition, I am significantly better than recursive functions without any pruning in space, because reducing recursion means reducing the occupation of stack space.
• Time complexity shall be calculated: