Abstract: the content of this article is my understanding in the process of learning Deep Learning, and the code is written by myself (the code ability is not very strong). If there is something wrong, you are welcome to point out and correct it.

Why use convolutional neural network

There are two problems when processing pictures using a fully connected network

1. Too many parameters (hollow - first hidden layer; solid - input layer):

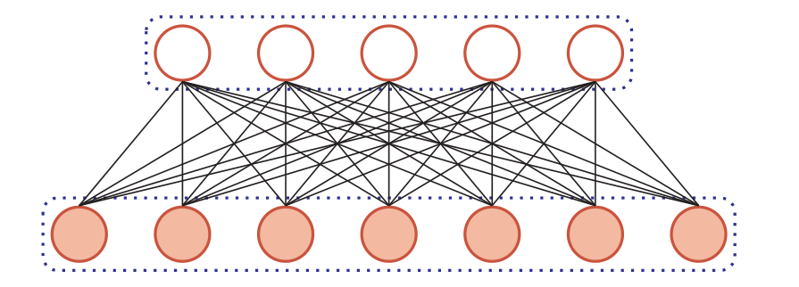
If the input picture is (100x100x3), each neuron in the hidden layer has 30000 independent connections to the input layer, and each connection corresponds to a weight parameter. In this way, with the increase of network scale, the number of parameters will rise sharply. This will make the training efficiency of the whole network very low and easy to over fit.

1. Local invariant feature: convolutional neural network has a receptive field mechanism similar to biology, which can better ensure the local invariance of the image.

At present, CNN is generally a feedforward neural network composed of Convolution layer, Pooling layer [also known as Pooling layer in some books] and full connection layer. The full connection layer is generally at the top of CNN.

CNN has three structural characteristics: local invariance, weight sharing and aggregation. These characteristics make CNN locally invariant to a certain extent and have fewer parameters than full connection.

Convolution

One dimensional convolution

Convolution in neural network is actually well understood, as shown in the following figure: (the following formula can be expressed in matrix form in two-dimensional processing)

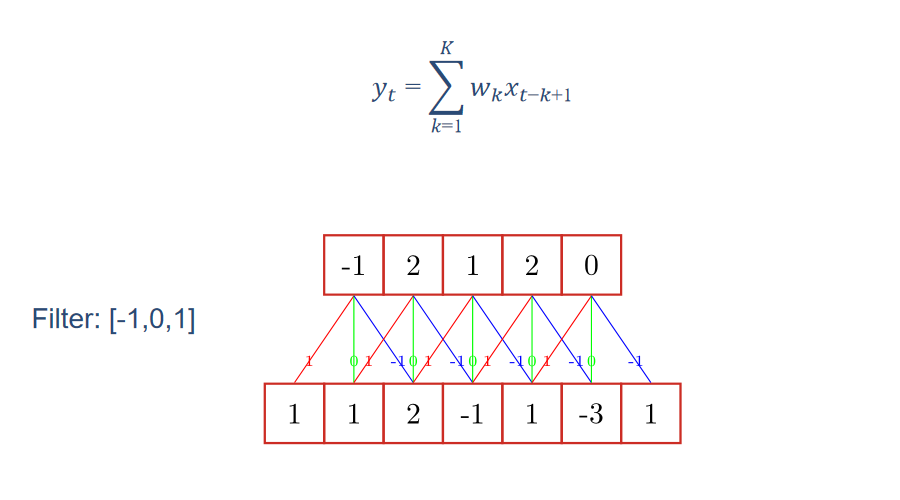
The Filter here is called Filter in signal processing and is our commonly used convolution kernel in CNN. The value of the convolution kernel [- 1,0,1] is the weight matrix. Given an input sequence (lower row) and a convolution kernel, an output sequence (upper row) can be obtained after convolution operation.

Different output sequences can be obtained by convoluting different convolution kernels with input sequences, that is, different features of input sequences can be extracted.

Two dimensional convolution

Since the image is a two-dimensional structure (with rows and columns), it is necessary to expand the convolution (the following figure shows the two-dimensional convolution operation):

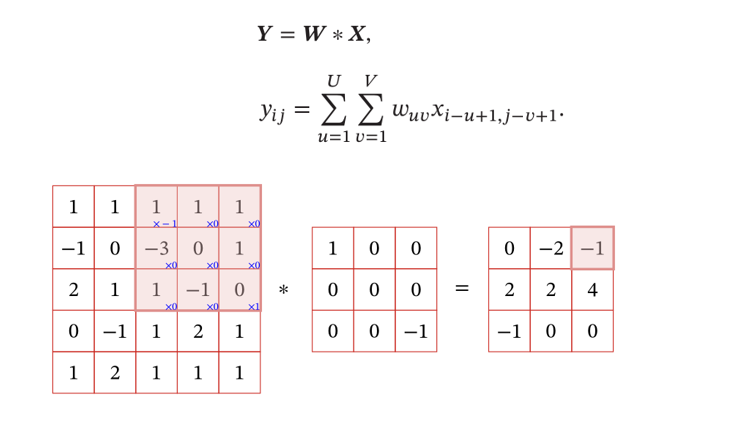
Bias bias can be added after the above formula;
Convolution kernel and bias are both learnable parameters.

In machine learning and image processing, the main function of convolution is to slide a convolution kernel on an image and get a set of new features through convolution. As shown below:

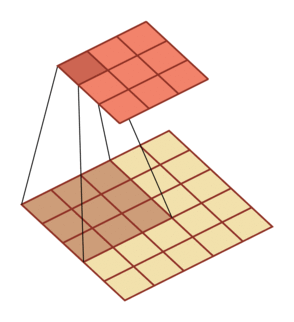
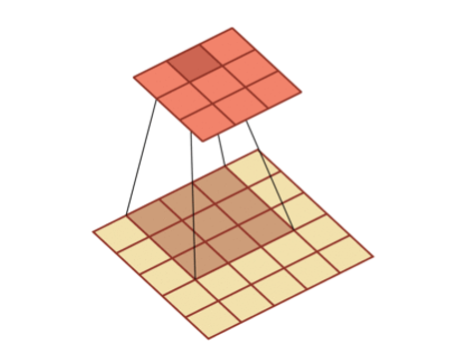
Step and padding

In convolution, we can also introduce the sliding step size and zero filling of convolution kernel to increase the diversity of convolution kernel, which can extract features more flexibly.

• Step size: the time interval of convolution kernel during sliding (figuratively speaking, the span during sliding)
• Zero filling: zero filling is performed at both ends of the input vector

As shown below:

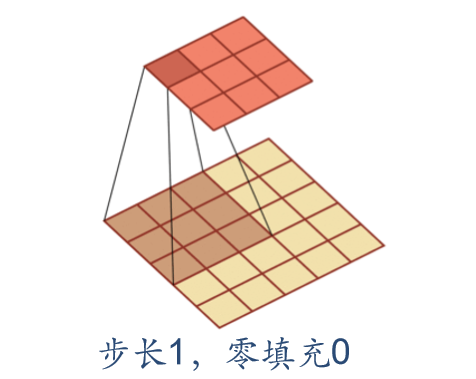
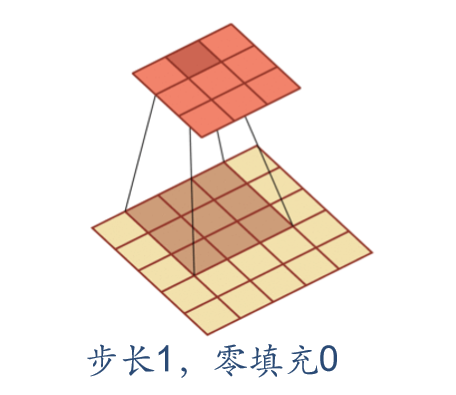
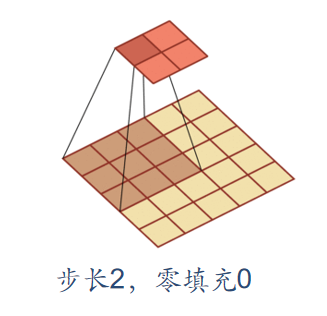
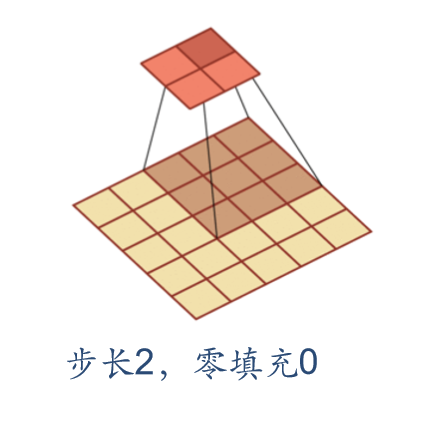
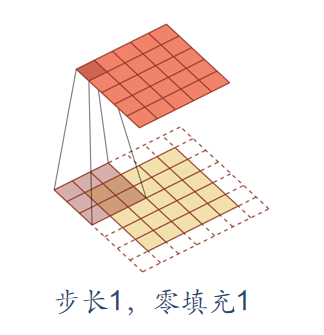
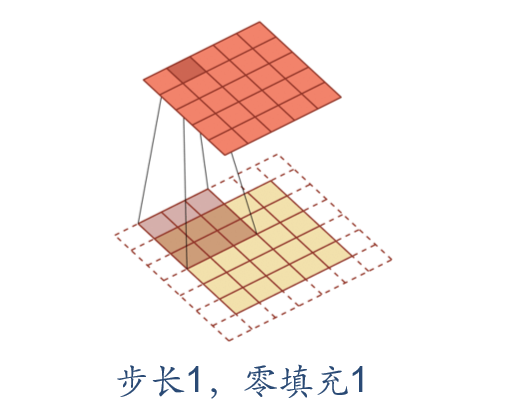
Convolutional neural network

According to the definition of convolution, convolution layer has two important properties:

1. Local connection
2. Weight sharing

Convolutional neural network uses convolution layer instead of full connection layer:

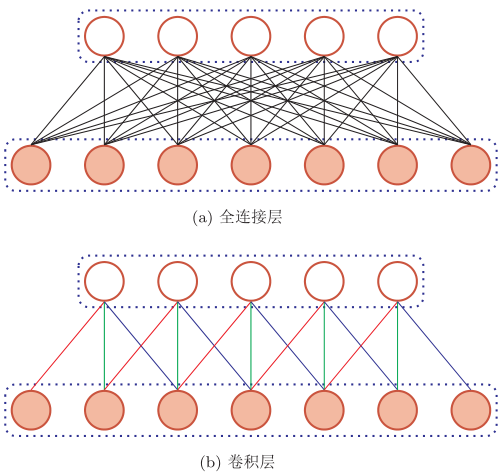
It can be seen that due to the characteristics of local connection of convolution layer, the parameters contained in convolution layer are much less than those in full connection layer.

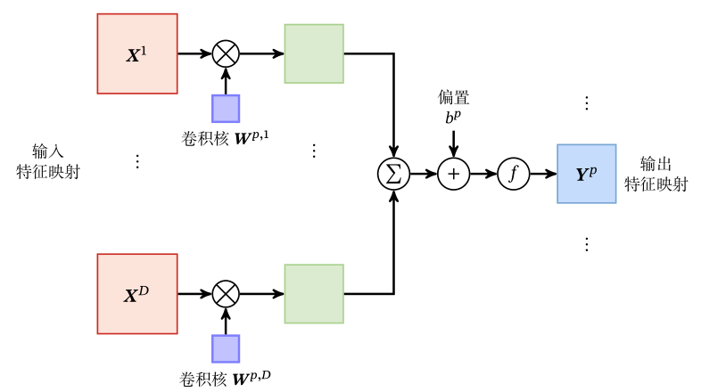
Weight sharing can be understood as a convolution kernel that captures only a specific local feature in the input data. Therefore, if you want to extract multiple features, you need to use multiple different convolution kernels (which can be clearly seen in the later three-dimensional way). As shown in the figure above, the weights on all connections of the same color are the same.

Due to local connection and weight sharing, the parameters of the convolution layer have only one k-dimensional weight W(l) and one-dimensional offset b(l), a total of K+1 parameters.

Convolution layer

The function of convolution layer is to extract the features of a local region. Different convolution kernels are equivalent to different feature extractors.

Because the image is a two-dimensional structure, in order to make full use of the local information of the image, neurons are usually organized into a three-dimensional neural layer with a size of height M x width N x depth D, which is composed of D feature maps of M x N size.

Feature mapping is the feature extracted by convolution of an image. Each feature mapping can be used as a class of extracted image features.

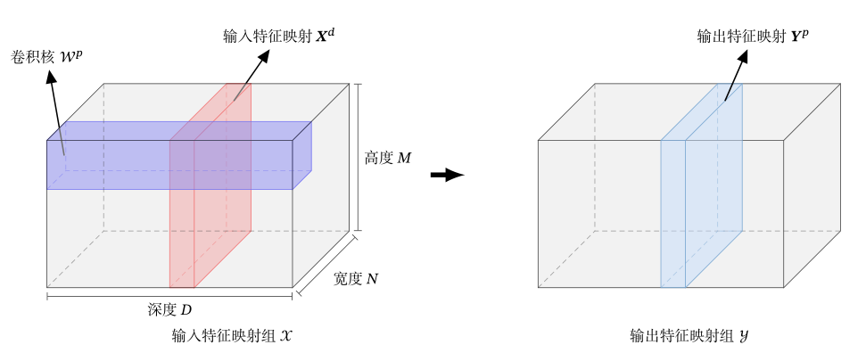
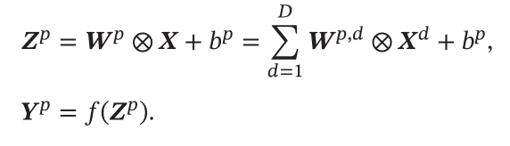
For example, for an RGB picture, the depth D in the above figure is the number of channels of the picture, and the height and width correspond to the size of the picture. There are three convolution kernels corresponding to the output of three feature maps Yp.

The calculation of feature mapping is shown in the following figure:

Pool layer (convergence layer)

Although the convolution layer can significantly reduce the number of connections in the network, the number of neurons in the feature mapping group is not significantly reduced. If followed by a classifier, its input dimension is still very high, and it is easy to have over fitting. Therefore, the pool layer is proposed.

The pooling layer, also known as sub sampling layer, is used to select features and reduce the number of features, so as to reduce the number of parameters.

Common pooling methods include:

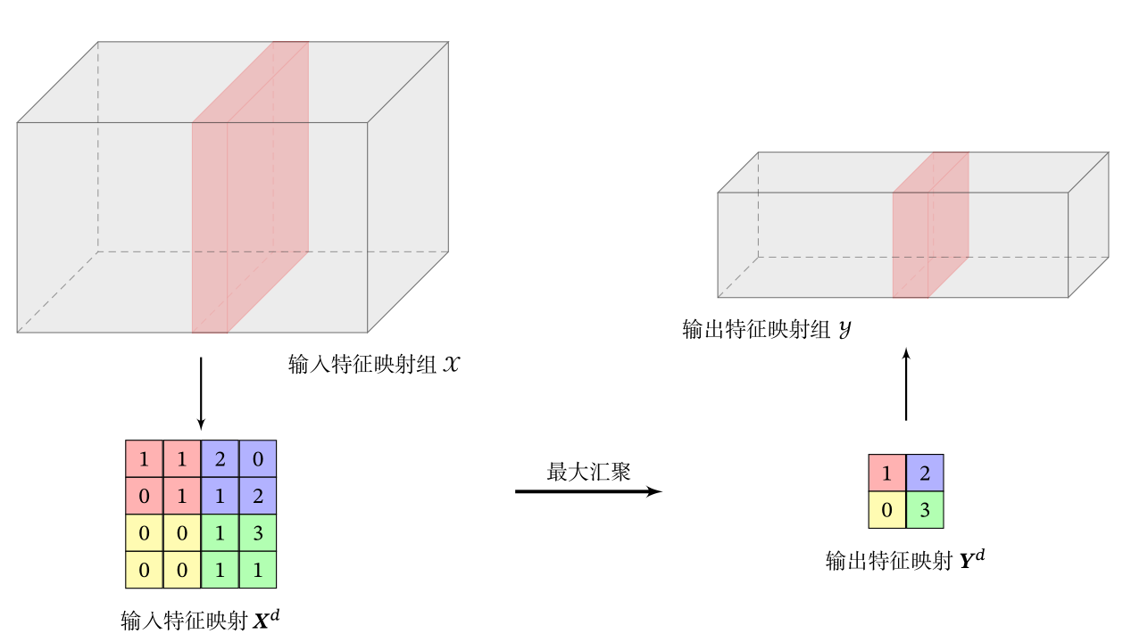
1. Max pooling: select the maximum activity value of all neurons in a region as the representation of this region.
2. Mean pooling: take the average value of neuronal activity in the region as the representation of this region.

The maximum pool is shown in the following figure:

Overall structure of convolutional network

The overall structure of convolution network commonly used at present is shown in the figure below:

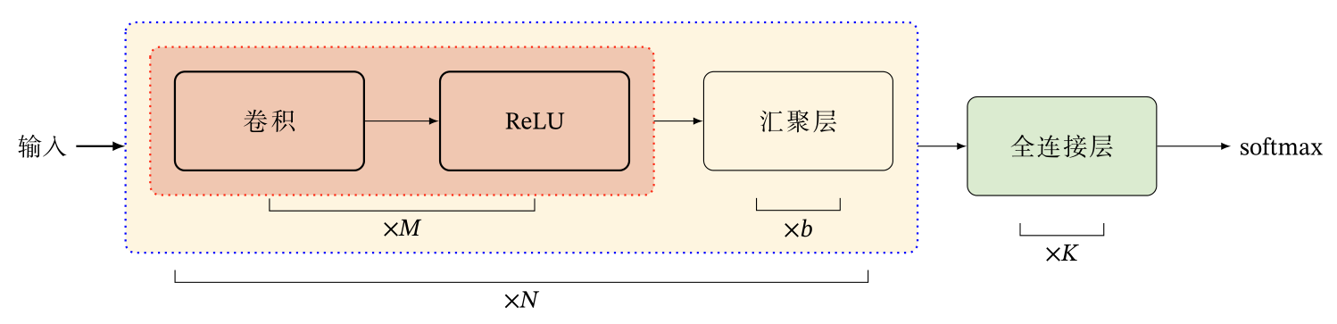
At present, the overall structure of convolution network tends to use smaller convolution kernel (the size of convolution kernel is generally odd) and deeper network structure.

In addition, because the operability of convolution layer is more and more flexible and the role of pooling layer is less and less, the popular convolution network tends to be full convolution network.

Residual net

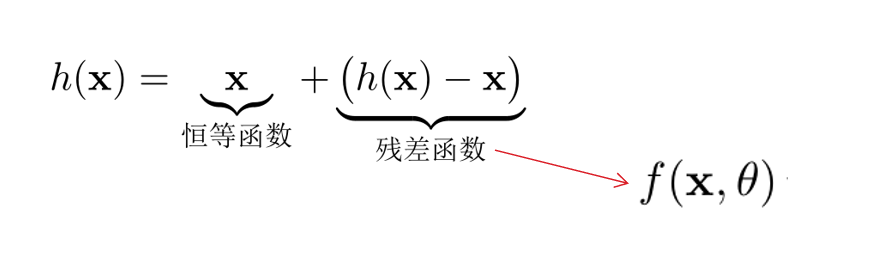
The residual network increases the propagation efficiency of information by adding direct edges to the nonlinear convolution layer.

• Suppose that in a deep network, we expect a nonlinear element (which can be one or more convolution layers) f(x, y) to approximate an objective function h(x).
• The objective function is divided into two parts: identity function and residual function

Residual unit:

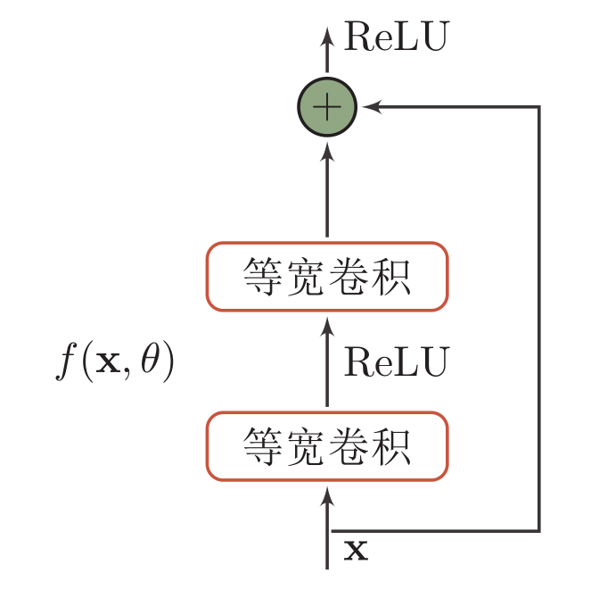
Residual network is a very deep network composed of many residual units in series.

Other convolution methods

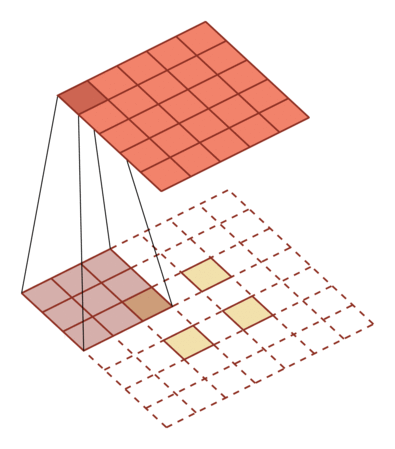
Transpose convolution -- mapping low dimensional features to high dimensions:

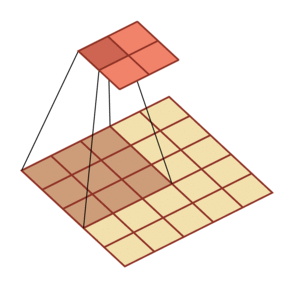
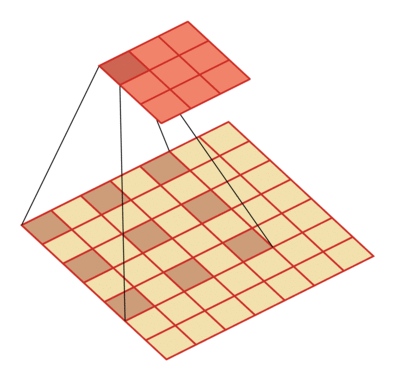
Void convolution - increase the size of the convolution kernel by inserting a "void":

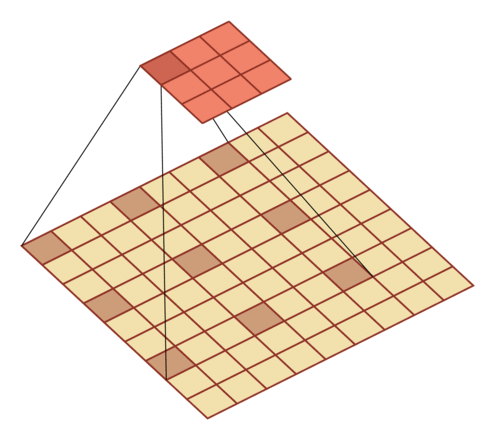
supplement

(1) We can:

• Increase the size of convolution kernel
• Increase the number of layers
• The convergence operation is performed before convolution

To increase the receptive field of the output unit

code

Environmental preparation:

• numpy
• anaconda
• Pycharm

One dimensional convolution

def Convolution_1d(input, kernel, padding=False, stride=1):

    input = np.array(input)
    kernel = np.array(kernel)
    kernel_size = kernel.shape[0]
    output = np.zeros((len(input) - kernel_size) // stride + 1)

    if padding:
        paddings = 1
        input_shape = len(input) + 2*paddings
        output = np.zeros((input_shape - kernel_size) // stride + 1)

    for i in range(len(output)):
        output[i] = np.dot(input[i:i+kernel_size], kernel)

    return output

Input:

input = [2,5,9,6,3,5,7,8,5,4,5,2,5,6,3,5,8,7,1,0,5,0,10,20,60]
print('input_len: ', len(input))
kernel = [1,-1,1]
print('kernel_len: ', len(kernel))
output = Convolution_1d(input=input, kernel=kernel)
print('output_len: ', len(output))
print('output: ',output)

Output results:

Two dimensional convolution

def Convolution_2d(input, kernel, padding=False, stride=1):

    input = np.array(input)
    kernel = np.array(kernel)
    stride = stride
    input_row = input.shape[0]
    input_col = input.shape[1]
    kernel_size = kernel.shape[0]
    output_row = (input_row - kernel_size) // stride + 1
    output_col = (input_col - kernel_size) // stride + 1
    output = np.zeros((output_row, output_col))

    if padding:
        padding=1
        input_row = input.shape[0]+2*padding
        input_col = input.shape[1]+2*padding
        output_row = (input_row-kernel_size) // stride + 1
        output_col = (input_col-kernel_size) // stride + 1
        output = np.zeros((output_row, output_col))

    for i in range(output_row):
        for j in range(output_col):
            output[i,j] = np.sum(input[i:i+kernel_size,j:j+kernel_size] * kernel)

    return output

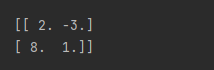
Input:

input = np.array([[2,7,3],[2,5,4],[9,4,2]])
kernel = np.array([[-1,1],[1,-1]])
output = Convolution_2d(input,kernel)
print('\n',output)

Output results:

Two dimensional convolution can also be realized by one-dimensional convolution, as long as some modifications are made to one-dimensional convolution.
High dimensional convolution can be realized by modifying two-dimensional convolution.

The code is a little sparse. Excuse me, excuse me