Quantitative basis of neural network
preface
This article is to sort out the code when reading the blog, in order to have a clearer understanding of the basic process of quantification.
This paper uses pytorch to build a basic network model manually, and the data set is mnist data set. I won't repeat it here, just look at the training code
Network model construction
1. Network structure
First, the structure of the defined network is described as follows:
class Net(nn.Module):
def __init__(self, num_channels=1):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(num_channels, 40, 3, 1)
self.conv2 = nn.Conv2d(40, 40, 3, 1, groups=20) # The error caused by quantization can be increased by using packet network
self.fc = nn.Linear(5*5*40, 10)
def forward(self, x): #
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 5*5*40)
x = self.fc(x)
return x
The implementation style is shown below and consists of two convolution layers and a linear layer.
Net( (conv1): Conv2d(1, 40, kernel_size=(3, 3), stride=(1, 1)) (conv2): Conv2d(40, 40, kernel_size=(3, 3), stride=(1, 1), groups=20) (fc): Linear(in_features=1000, out_features=10, bias=True) )
2. Network training
python
from model import *
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
import os
import os.path as osp
def train(model, device, train_loader, optimizer, epoch):
model.train()
lossLayer = torch.nn.CrossEntropyLoss()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = lossLayer(output, target)
loss.backward()
optimizer.step()
if batch_idx % 50 == 0:
print('Train Epoch: {} [{}/{}]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset), loss.item()
))
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
lossLayer = torch.nn.CrossEntropyLoss(reduction='sum')
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += lossLayer(output, target).item()
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {:.0f}%\n'.format(
test_loss, 100. * correct / len(test_loader.dataset)
))
if __name__ == "__main__":
batch_size = 64
test_batch_size = 64
seed = 1
epochs = 15
lr = 0.01
momentum = 0.5
save_model = True
using_bn = False
torch.manual_seed(seed)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, num_workers=1, pin_memory=True
)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=test_batch_size, shuffle=True, num_workers=1, pin_memory=True
)
if using_bn:
model = NetBN().to(device) #Home BN network model
else:
model = Net().to(device) #The network model without BN is adopted
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum)
for epoch in range(1, epochs + 1):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
if save_model:
if not osp.exists('ckpt'):
os.makedirs('ckpt')
if using_bn:
torch.save(model.state_dict(), 'ckpt/mnist_cnn.pt')
else:
torch.save(model.state_dict(), 'ckpt/mnist_cnn.pt')
After training the network model, you will get a weight file, namely ckpt/mnist_cnnbn.pt.
3. Test the training model
Firstly, we load the weight, and then calculate the accuracy of the model in the case of full accuracy.
def full_inference(model, test_loader):
correct = 0
for i, (data, target) in enumerate(test_loader, 1):
output = model(data)
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
print('\nTest set: Full Model Accuracy: {:.0f}%\n'.format(100. * correct / len(test_loader.dataset)))
batch_size = 64
using_bn = False
if __name__ == "__main__":
batch_size = 64
using_bn = False
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, num_workers=1, pin_memory=True
)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=False, num_workers=1, pin_memory=True
)
if using_bn:
model = NetBN()
model.load_state_dict(torch.load('ckpt/mnist_cnnbn.pt', map_location='cpu'))
else:
model = Net()
model.load_state_dict(torch.load('ckpt/mnist_cnn.pt', map_location='cpu'))
model.eval()
full_inference(model, test_loader)
The next step is our quantification of the model. This paper mainly adopts the post quantization method.
4. Basic quantization function
4.1 calculation of scale factor and zero point
First, we need to implement the basic formula of quantization. They calculate the scale and zero point respectively.
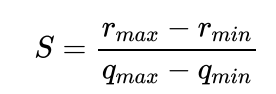
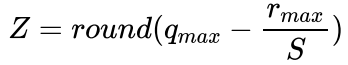
Its code is as follows:
"""
Calculate quantization scale and zero
:min_val: minimum value
:scale: Maximum
:num_bits: Quantized bit position
:returns: Quantitative scale; zero point
"""
def calcScaleZeroPoint(min_val, max_val, num_bits=8):
qmin = 0.
qmax = 2. ** num_bits - 1.
scale = float((max_val - min_val) / (qmax - qmin))
zero_point = qmax - max_val / scale
if zero_point < qmin:
zero_point = qmin
elif zero_point > qmax:
zero_point = qmax
zero_point = int(zero_point)
return scale, zero_point
"""
This is right tensor Quantify
:x: Input to be quantified tensor
:scale: Quantitative scale
:zero_point: zero point
:num_bits: Quantized bit position
:signed: Is quantization signed or not
:returns: Tensor after quantization
"""
def quantize_tensor(x, scale, zero_point, num_bits=8, signed=False):
if signed:
qmin = - 2. ** (num_bits - 1)
qmax = 2. ** (num_bits - 1) - 1
else:
qmin = 0.
qmax = 2.**num_bits - 1.
q_x = zero_point + x / scale #Calculate the quantized value
q_x.clamp_(qmin, qmax).round_() #round stands for rounding
return q_x #Quantized value
"""
This is right tensor Inverse quantization
:x: Quantized value
:scale: Quantitative scale
:zero_point: zero point
:returns: Output tensor after inverse quantization
"""
def dequantize_tensor(q_x, scale, zero_point):
return scale * (q_x - zero_point)
4.2 solving the maximum and minimum values
It can be seen from the above formula that if we want to calculate the scale factor and zero to realize the quantization of the value, we need to know the maximum and minimum values of the value and the quantized bits. Therefore, in the post training quantization process, it is necessary to count the samples and the min and max of the middle layer, and some quantization and inverse quantization operations are frequently involved. Therefore, we can package these functions into a QParam class. The code is as follows:
"""
QParam In the process of post training quantification,It is necessary to make statistics on the samples and the of the middle layer first min, max,It is also frequently involved
To some quantification,Inverse quantization operation,So we can package all these functions into one QParam class
:num_bits: Bit
:scale: Quantitative scale
:min: minimum value
:max: Maximum
"""
class QParam:
def __init__(self, num_bits=8):
self.num_bits = num_bits
self.scale = None
self.zero_point = None
self.min = None #Manually defined maximum
self.max = None #Manually defined minimum
"""
update Function is used for statistics min,max
"""
def update(self, tensor):
if self.max is None or self.max < tensor.max():
self.max = tensor.max()
self.max = 0 if self.max < 0 else self.max
if self.min is None or self.min > tensor.min():
self.min = tensor.min()
self.min = 0 if self.min > 0 else self.min
#Calculate the quantization scale and zero of the parameters
self.scale, self.zero_point = calcScaleZeroPoint(self.min, self.max, self.num_bits)
def quantize_tensor(self, tensor):
return quantize_tensor(tensor, self.scale, self.zero_point, num_bits=self.num_bits)
def dequantize_tensor(self, q_x):
return dequantize_tensor(q_x, self.scale, self.zero_point)
The defined class can realize the quantization operation of data. Its main operation steps are: first, use the update() function to calculate the maximum and minimum values of the input tensor, and call the function calcScaleZeroPoint() to calculate the scale factor and zero point (this is the specific implementation process of Formula 1). Then, the numerical value is quantized, and the function used is quantize_tensor(), which is the specific implementation process of formula 2. QParam also defines a method for inverse quantization, quantify_ tensor().
It should be noted that except for the min and max of the first conv, all other layers only need to count the min and max of the intermediate output feature. In addition, for activation functions such as relu and maxpooling, they will follow the min and max output from the previous layer without additional statistics, that is, the same min and Max will be shared in the above figure.
The following is the framework of the quantization module.
5. Network quantization module
We need to define some basic quantization modules to call convolution, full connection, Relu and pooling layers. First, we need to define a quantization base class, which can reduce some duplicate codes and make the structure of the code clearer.
class QModule(nn.Module):
def __init__(self, qi=True, qo=True, num_bits=8):
super(QModule, self).__init__()
if qi:
self.qi = QParam(num_bits=num_bits) #
if qo:
self.qo = QParam(num_bits=num_bits)
"""
freeze The second is freeze function,This function is mainly the calculation formula (4) in M,q_w,q_b
"""
def freeze(self):
pass
def quantize_inference(self, x):
raise NotImplementedError('quantize_inference should be implemented.')
This base class defines the methods to be provided by each quantization module.
First__ init__ Function, which specifies not only the number of bits to be quantized, but also whether to provide quantized input (qi) and output (qo). At the same time, as mentioned earlier, not every network needs to count the input min and max. most middle layers use the qo of the upper layer as their own qi.
The second is the free function, which will play a role after the statistics of min and max. As mentioned above, many items in formula (4) can be calculated in advance. freeze fixes these items in advance and converts the weight of the network from floating-point real numbers to fixed-point integers.