I first came into contact with 1stOpt because I needed to solve a set of very complex differential equations N years ago, and I was too lazy to knock the code with matlab, so I searched the Internet for a more easy and convenient way. I found 1stOpt as soon as I looked. Although it is a green and harmonious version, it can basically meet my needs. I read all the help documents of 1stOpt.

After reading the introduction of 1stOpt's official website, it is said that 1stOpt is a comprehensive mathematical optimization tool that does not depend on the initial value. Even the old brands of Matlab, Origin, Lingo and Gams are amazed, thanks to its general global optimization algorithm. Not relying on the initial value is extremely useful for scientific calculation. For example, problems such as root finding, solving differentiation and optimization often rely on the initial value. Improper selection of the initial value may get high error or even wrong results, and 1stOpt perfectly solves this problem. It has been widely used in engineering, finance, decision-making, circulation, production and other analysis, calculation and planning fields. Including: automatic model optimization and calibration; Parameter estimation; Arbitrary model formula, linear, nonlinear fitting, regression; Solving nonlinear continuous equations; Solving ordinary differential equations (Systems) (initial value and boundary value problems); Fitting and solving ordinary differential equations (Systems); Complex equation solving and complex nonlinear fitting; Arbitrary dimensional function, implicit function, extremum solution; Solving the root of implicit function, drawing and finding the extreme value; Linear, nonlinear and integer programming; Combinatorial optimization problem, etc.

Let's take a look at the strength of 1stOpt through several examples:

Special note: the English trial version of 1stOpt 5.5 adopted this time is all from the 5.0 official help documents.

Because the trial version has a limit on the number of parameters, the calculation parameters cannot exceed 4. At present, the latest official version is 8.0, and version 9.0 will be released soon. Let's take a look.

1. Two dimensional needle global optimal function

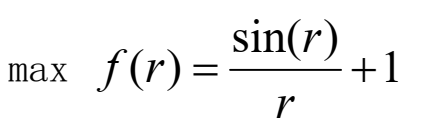
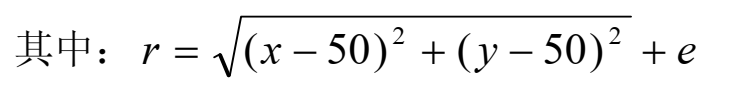
The function graph of the function is as follows. The global maximum value of 1.1512 is obtained at (50,50), and its second maximum value is 1.12837. It is a multi peak function, and the global best can hardly be found by traditional optimization methods.

1stOpt source code:

Parameter x[0,100], y[0,100];
ConstStr r = sqrt((x-50)^2+(y-50)^2)+exp(1);
MaxFunction Sin(r)/r + 1;

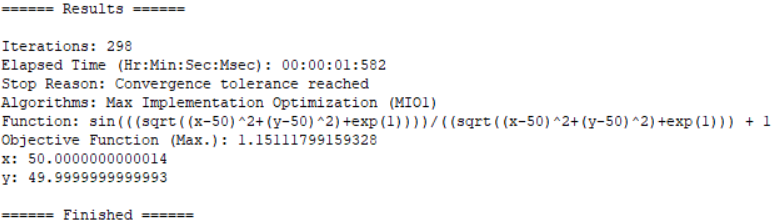
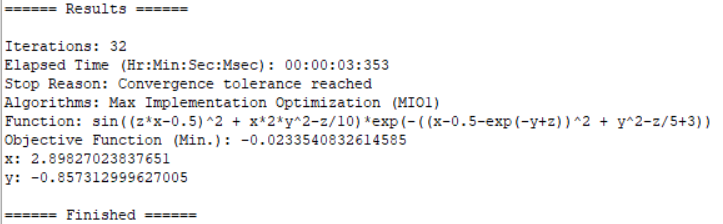
2. Implicit function optimization

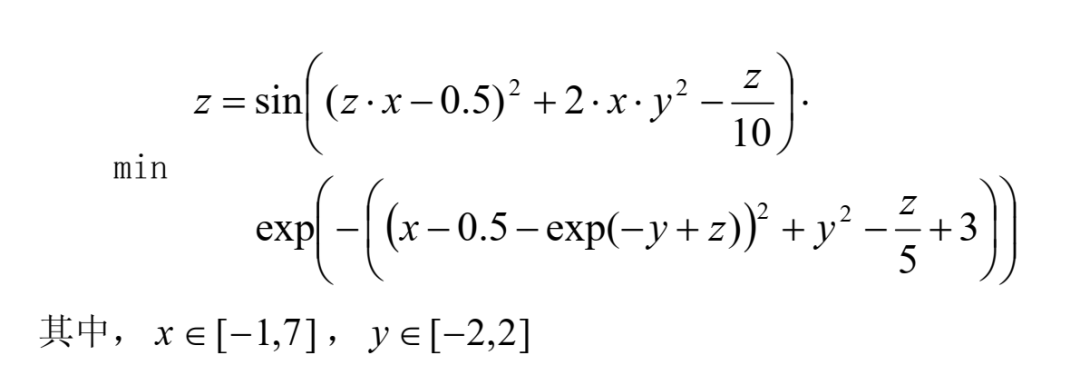
1stOpt source code:

Parameter x[-1,7], y[-2,2];
Minimum = z;
Function z = sin((z*x-0.5)^2 + x*2*y^2-z/10)*exp(-((x-0.5-exp(-y+z))^2 + y^2-z/5+3));

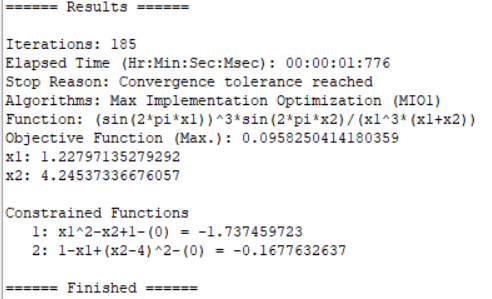
3. Nonlinear programming

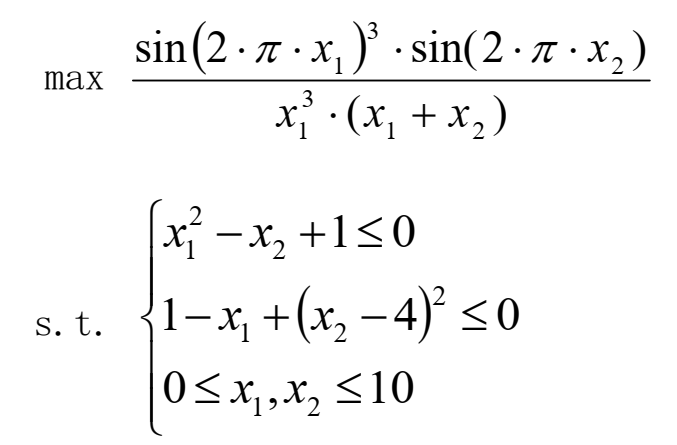
1stOpt source code:

Parameter x1[0,10], x2[0,10];
MaxFunction (sin(2*pi*x1))^3*sin(2*pi*x2)/(x1^3*(x1+x2));
x1^2-x2+1 <= 0;
1-x1+(x2-4)^2 <= 0;

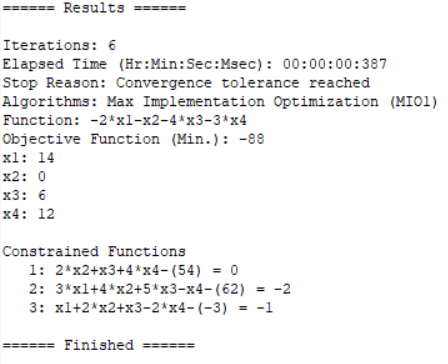
4. Integer programming

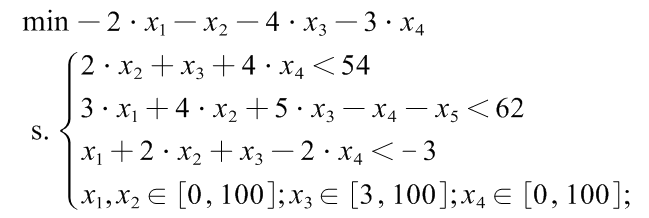
1stOpt source code:

Parameter x(1:2)[0,100,0], x3[3,100,0], x4[0,100,0];
MinFunction -2*x1-x2-4*x3-3*x4;
2*x2+x3+4*x4<54;
3*x1+4*x2+5*x3-x4<62;
x1+2*x2+x3-2*x4<-3;

5. Optimization problems with equality constraints

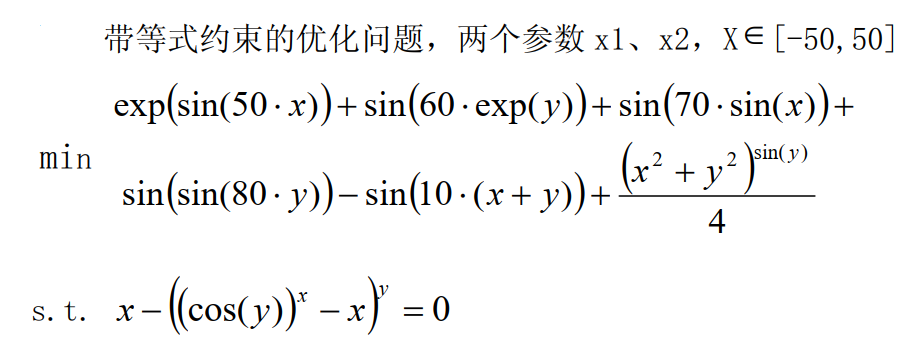
1stOpt source code:

Algorithm = DE1[100];
PenaltyFactor = 5;
ParameterDomain = [-50,50];
MinFunction exp(sin(50*x)) +sin(60*exp(y)) +sin(70*sin(x))
+sin(sin(80*y))-sin(10*(x+y))+(x^2+y^2)^sin(y)/4;
x-((cos(y))^x-x)^y<=0;

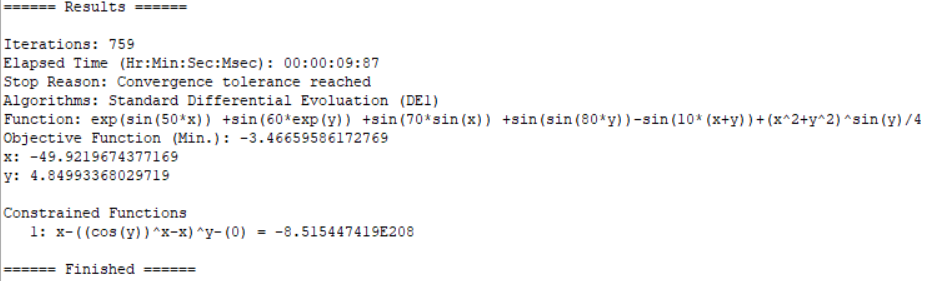
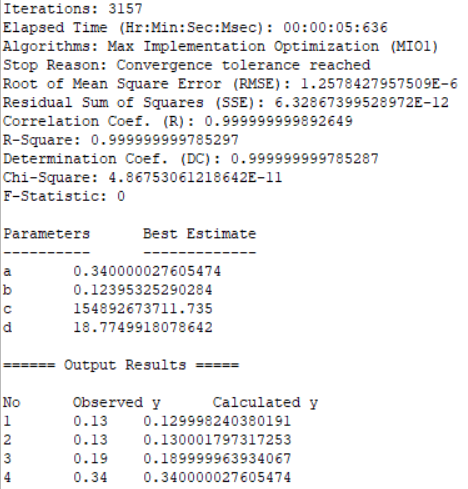
6. Nonlinear fitting

The National Institute of standards and Technology (NIST) provides a set of 27 nonlinear fitting test questions. Almost all famous data analysis software packages in the world take passing the set of test questions as the verification standard. Through comparative test, 1stOpt is the only software package that does not rely on the initial value provided by NIST, but can obtain all the optimal solutions with any random initial value (if the initial value provided by NIST is used, the optimal solution can be obtained more easily). In practical application, it is very difficult to select and determine a reasonable initial value group, especially when there are many parameters. In this sense, the practical ability of 1stOpt has reached the industry-leading level.

Example code:

Variables x, y;
Parameters a, b, c, d;
Function y = a-b*exp(-c*x^d);
Data;
0.05 0.13
0.15 0.13
0.25 0.19
0.35 0.34

7. Solving systems with integral equations

This question comes from small wood insect. Due to parameter limitation, it is changed to 4 parameters:

http://muchong.com/t-4192342-1-authorid-8600892

Parameters a,b,c,d;
Function int(exp(a+b*x+c*x^2+d*x^3),x=0.5779,13.5883)=1;
int(x*exp(a+b*x+c*x^2+d*x^3),x=0.5779,13.5883)=6.86;
int(x^2*exp(a+b*x+c*x^2+d*x^3),x=0.5779,13.5883)=54.39;
int(x^3*exp(a+b*x+c*x^2+d*x^3),x=0.5779,13.5883)=478.14;

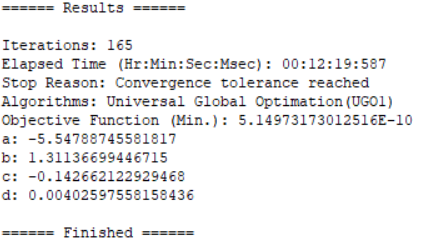
Due to the limitation of functions and parameters, it is impossible to demonstrate the more powerful solution function of 1stOpt. Let's demonstrate it here for the time being.