Author: Wu Zhichun

Continued JavaScript digital storage We know why 0.1 + 0.2 ≠ 0.3 and find a problem. Let's solve the problem this time.

Analyze problems

Before solving the problem, let's find out the root cause of the problem. The root of the problem is that the integer is too large; Decimal is because there is an invalid cycle when converting decimal to binary. Due to the limitation of storage digits, there is "rounding", and the loss of precision occurs,. See the previous article for details JavaScript digital storage.

Solution

For integers, the probability of front-end problems may be relatively low. After all, very few businesses need to use very large integers, as long as the operation result does not exceed math Pow (2, 53) will not lose accuracy.

For decimals, there are still many chances of problems at the front end, especially when some e-commerce websites involve data such as amount. Solution: put the decimal to the integer (multiply by multiple), and then reduce it back to the original multiple (divide by multiple).

example

Calculated decimal: 0.1 + 0.02

Calculation scheme: put the decimal place into an integer (multiply multiple), and then reduce it back to the original multiple (divide multiple).

Calculation process

The first step is to expand the decimal to an integer

0.1 expand 10 times to 1

0.02 expand 100 times to 2

Step 2 Calculation

1 * 100 ÷10 + 2 = 12

Step 3 reduction multiple (divided by the maximum multiple)

12 ÷ 100 = 0.12

We've probably sorted out the calculation process. Now we use code to implement the whole process

code implementation

Analyzing the above three steps, our code implementation is divided into two steps.

First step

To obtain two integer values, two multiplier values, and the maximum multiplier value from two numbers.

For example:

The input parameters are 0.1 and 0.02

The return value should be an integer value of 0.1, with a multiple of 10; The integer value of 0.02 is 2 times the value of 100.

The code is implemented as follows

 /**
   * Determine whether num is an integer
   * @param {number|string|null} value
   */
  isInteger = (value) => {
    if (isNaN(value)) return false;
    const num = +value;

    return Math.floor(num) === num;
  };  

  /**
   * Converts a floating-point number to an integer and returns an integer and a multiple
   * @param {number|string|null} floatNum For example: 3.14
   * @returns {object} For example: {times:100, num: 314}
   */
toInteger = (floatNum) => {
    const ret = { times: 1, num: 0 };
    if (this.isInteger(floatNum)) {
      ret.num = floatNum;
      return ret;
    }
    const strfi = `${floatNum}`;
    const dotPos = strfi.indexOf('.');
    const len = strfi.substr(dotPos + 1).length;
    const times = 10 ** len;
    ret.times = times;
    ret.num = +strfi.replace('.', '');

    return ret;
  };

The second step is to use integer value and multiple calculation results

The code is as follows

 add = (prevValue, nextValue) => {
    let result = null;
    //initialization
    const objectNumberA = this.toInteger(prevValue);
    const objectNumberB = this.toInteger(nextValue);
    const numberA = objectNumberA.num;
    const numberB = objectNumberB.num;
    const timesA = objectNumberA.times;
    const timesB = objectNumberB.times;
    const timesMax = timesA > timesB ? timesA : timesB;

    //Computational addition
    if (timesA === timesB) {
      // The two decimal places are the same length
      result = numberA + numberB;
    } else if (timesA > timesB) {
      // numberA decimal places are longer than numberB
      result = numberA + numberB * (timesA / timesB);
    } else {
      // numberA decimal place length is less than numberB
      result = numberA * (timesB / timesA) + numberB;
    }

    //Zoom out and return value
    return result / timesMax;
  };

Code test

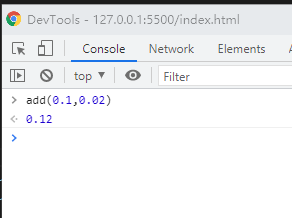
In this way, we can solve the problem of losing precision in decimal addition.

Similarly, we can realize subtraction, multiplication and division. Specific implementation code into the next, it is recommended to try their own implementation on the basis of addition.

subtraction

 subtract = (prevValue, nextValue) => {
    let result = null;
    //initialization
    const objectNumberA = this.toInteger(prevValue);
    const objectNumberB = this.toInteger(nextValue);
    const numberA = objectNumberA.num;
    const numberB = objectNumberB.num;
    const timesA = objectNumberA.times;
    const timesB = objectNumberB.times;
    const timesMax = timesA > timesB ? timesA : timesB;
    
    //Computational subtraction
    const { numberA, numberB, timesA, timesB, timesMax } = calcuNumber;
    if (timesA === timesB) {
      result = numberA - numberB;
    } else if (timesA > timesB) {
      result = numberA - numberB * (timesA / timesB);
    } else {
      result = numberA * (timesB / timesA) - numberB;
    }
    
		//Zoom out and output
    return result / timesMax;
  };

multiplication

 multiply = (prevValue, nextValue) => {
   //initialization 
   	const objectNumberA = this.toInteger(prevValue);
    const objectNumberB = this.toInteger(nextValue);
    const numberA = objectNumberA.num;
    const numberB = objectNumberB.num;
    const timesA = objectNumberA.times;
    const timesB = objectNumberB.times;
    const timesMax = timesA > timesB ? timesA : timesB;
    
		//Calculate multiplication, reduce and output
    return (numberA * numberB) / (timesA * timesB);
  };

division

divide = (prevValue, nextValue) => {
    //initialization 
   	const objectNumberA = this.toInteger(prevValue);
    const objectNumberB = this.toInteger(nextValue);
    const numberA = objectNumberA.num;
    const numberB = objectNumberB.num;
    const timesA = objectNumberA.times;
    const timesB = objectNumberB.times;
    const timesMax = timesA > timesB ? timesA : timesB;
    
		//Calculate the division, reduce and output
    return (numberA / numberB) * (timesB / timesA);
  };

We find that the initialization code will be repeated. We can take it out and make it into a common method. This step is up to you.