First of all, I'd like to share my personal experience. I'm a graduate of 2021. I'm an ordinary undergraduate. I'm a non computer major. After being beaten by spring moves, I've successfully landed in a large factory and joined the post. It is necessary for Internet companies to have a recruitment algorithm. If the basic algorithm fails to pass the written test, I can't pass the written test. Before school recruitment, I brushed 100 + algorithm questions in leetcode, sorted out some of my own notes and shared them with people in need. Personally, I think the learning of data structure and algorithm is still very important, especially for non professional programmers like me. The content is not very perfect. You can also add it in the message area.
data structure
1. Stack
1.1 overview of stack
Stack, which is a restricted linear property, last in first out (LIFO)
-
The limitation is that insert and delete operations are only allowed at one end of the table. This end is called the top of the stack, and the other end is called the bottom of the stack
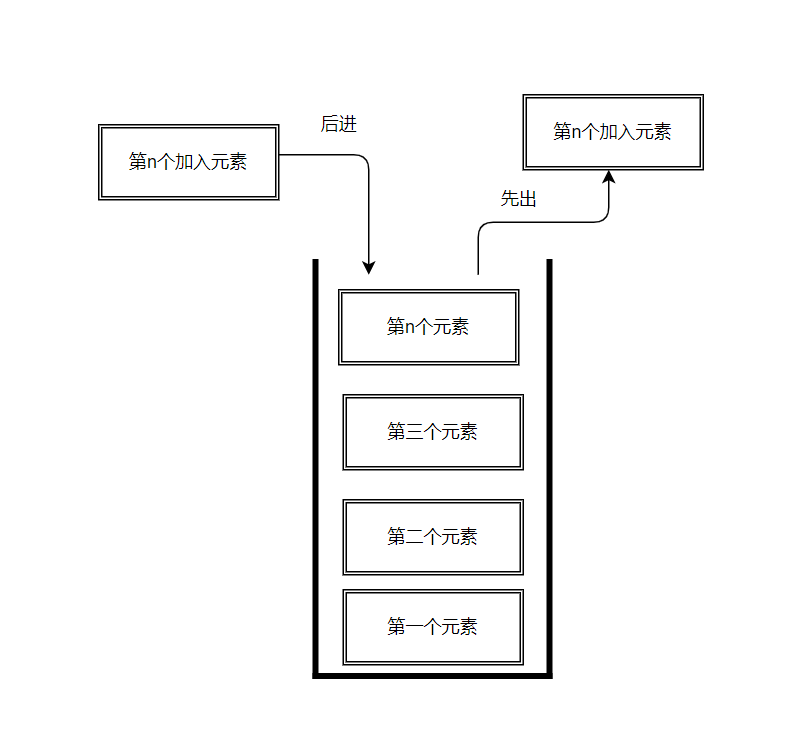
1.2 general operation of stack
| method | effect |
|---|---|
| push(e) | Add a new element to the top of the stack |
| pop() | Remove the top element of the stack and return the removed element |
| peek() | Returns the top element of the stack without making any changes to the stack |
| isEmpty() | If there is no element in the stack, it returns true; otherwise, it returns false |
| size() | Returns the number of elements in the stack. This method is similar to the length of an array |
| toString() | Returns the contents of the stack structure as a string |
1.3 encapsulating stack with js
function Stack(){
this.stack = []
}
Stack.prototype.push=function(element) {
this.stack.push(element)
}
Stack.prototype.pop=function(){
return this.stack.pop()
}
Stack.prototype.size=function(){
return this.stack.length
}
Stack.prototype.peek=function(){
return this.stack[this.size()-1]
}
Stack.prototype.isEmpty=function() {
return this.size === 0 ? true : false
}
Stack.prototype.toString=function(){
return this.stack.join(' ')
}
1.4 application of stack
Valid parentheses,Maximum number of queues,Minimum stack
2. Queue
2.1 overview of queues
Queue, which is a restricted linear property, first in first out (LIFO)
- The restriction is that deletion is only allowed at the front end of the table and insertion is allowed at the back end of the table
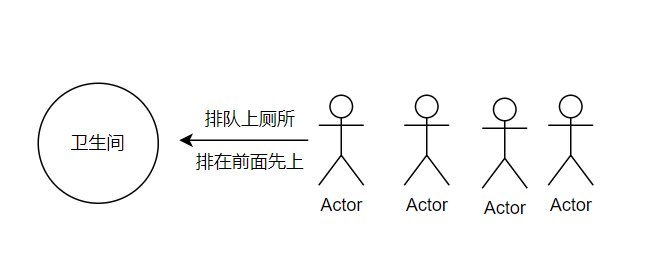
2.2 general operation of queue
| method | effect |
|---|---|
| enqueue(e) | Add one or more new elements to the end of the queue |
| dequeue() | Remove the first element of the queue and return the removed element |
| front() | Returns the first element of the queue without any modification to the queue |
| isEmpty() | If there are no elements in the queue, it returns true; otherwise, it returns false |
| size() | Returns the number of elements in the queue. This method is similar to the length of an array |
| toString() | Returns the contents of the queue as a string |
2.3 encapsulating queues with js
function Queue(){
this.queue = []
}
Queue.prototype.enqueue = function(ele){
this.queue.push(ele)
}
Queue.prototype.dequeue = function(){
return this.queue.shift()
}
Queue.prototype.front = function(){
return this.queue[this.size() -1]
}
Queue.prototype.size = function(){
return this.queue.length
}
Queue.prototype.front = function(){
return this.size === 0
}
Queue.prototype.toString = function(){
return this.queue.join('')
}
2.4 application of queue
Design cyclic queue,Design Dual Ended queue,Number of recent requests
3. Linked list
3.1 overview of linked list
Linked List: a Linked List is an abstract data type that consists of a set of memory structure nodes that do not have to be connected [do not have to be connected: can be continuous or discontinuous] and are linked together in a specific order.
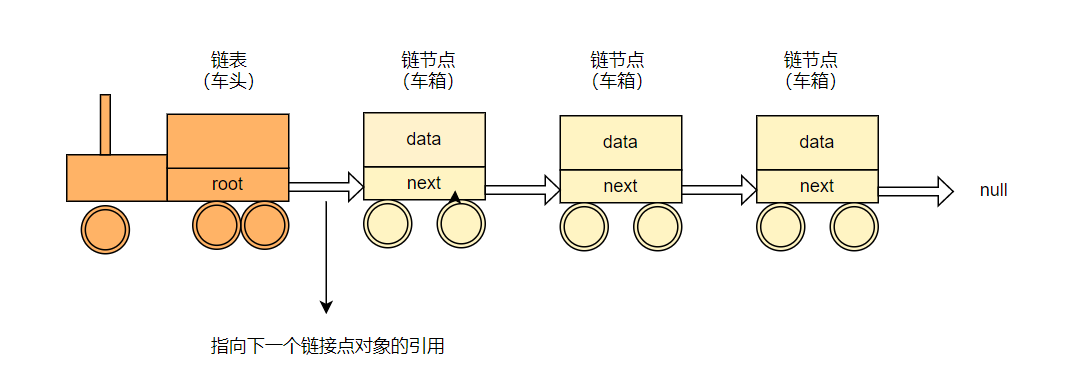
3.2 general operation of linked list
| method | effect |
|---|---|
| append(ele) | Add an element to the end of the linked list |
| insert(index,ele) | Insert a new item into a specific location in the linked list |
| get(index) | Get the element of the corresponding position |
| indexOf(ele) | Returns the index of the first matching element of the element in the linked list. If not, returns - 1 |
| update(index) | Modify an element at a location |
| removeAt(index) | Removes the current element from a specific location in the linked list |
| remove(ele) | Remove the element from the linked list |
| isEmpty() | If there are no elements in the linked list, return true; otherwise, return false |
| size() | Returns the number of elements contained in the linked list. Similar to the length attribute of an array |
| toString() | Because the linked list uses the Node class, you need to override the toString() method to output only the value of the element |
3.3 encapsulate linked list with js
function LinkedList (){
//Chain header
this.head = null
this.length = 0
}
// Create linked list node
function Node(data){
this.data = data
this.next = null
}
LinkedList.prototype.append = function(data){
let newNode = new Node(data)
if(this.length === 0){
this.head = newNode
}else{
let currentNode = this.head
while(currentNode.next){
currentNode = currentNode.next
}
currentNode.next = newNode
}
this.length += 1
}
LinkedList.prototype.insert = function(index, data){
let newNode = new Node(data)
if(index < 0 || index > this.length) return false
//The inserted node is the first
if(index === 0){
newNode.next = this.head
this.head = newNode
}else{
let currentNode = this.head,
curIndex = 0,
previous = null
while(curIndex ++ < index){
previous = currentNode
currentNode = currentNode.next
}
newNode.next = currentNode
previous.next = newNode
}
this.length ++
return true
}
LinkedList.prototype.get = function(index){
if(index < 0 || index > this.length) return null
let curNode = this.head,
curIndex = 0
while(curIndex++ < index){
curNode = curNode.next
}
return curNode.data
}
LinkedList.prototype.indexOf = function(item){
let curNode = this.head,
curIndex = 0
while(curNode){
curNode = curNode.next
if(curNode && curNode.data == item){
return curIndex
}
}
return -1
}
LinkedList.prototype.update = function(index, item){
if(index < 0 || index > this.length) return false
let curNode = this.head,
curIndex = 0
while(curIndex++ < index){
curNode = curNode.next
}
curNode.data = item
}
LinkedList.prototype.removeAt = function(index){
if(index < 0 || index > this.length) return null
if(index === 0){
this.head = null
}else{
let curNode = this.head,
previous = null,
curIndex = 0
while(curIndex++ < index){
previous = curNode
curNode = curNode.next
}
previous.next = curNode.next
}
this.length --
}
LinkedList.prototype.remove = function(data){
let index = this.indexOf(data)
this.removeAt(index)
}
LinkedList.prototype.isEmpty = function(){
return this.length > 0 ? true : false
}
LinkedList.prototype.toString = function() {
let res = '',
currentNode = this.head
while(currentNode){
res += currentNode.data
currentNode = currentNode.next
}
return res
}
3.4 application of linked list
Add two numbers,Merge k ascending linked lists,Rotating linked list,Separate linked list
4. Assemble
4.1 overview of collection
A collection is usually made up of a set of elements that are out of order and cannot be repeated. Cannot be accessed by subscript
4.2 general operation of collection
| method | effect |
|---|---|
| add(value) | Add an element to the collection |
| remove(value) | Remove an element from the collection |
| has(value) | Returns true if in the collection, false otherwise |
| clear() | Remove all items from the collection |
| size() | Returns the number of elements contained in a collection, similar to the length attribute of an array |
| values() | Returns an array containing all the values of the collection |
4.3 encapsulating collections with js
function Set(){
this.items = {}
}
Set.prototype.add = function(value){
if(this.has(value)) return false
this.items[value] = value
return true
}
Set.prototype.has = function(value){
return this.items.hasOwnProperty(value)
}
Set.prototype.remove = function(value){
if(!this.has(value)) return false
delete this.items[value]
return true
}
Set.prototype.clear = function(){
this.items = {}
}
Set.prototype.size = function(){
return Object.keys(this.items).length
}
Set.prototype.values = function(){
return Object.keys(this.items)
}
4.4 application of set
Delete duplicate elements in the array,There are duplicate elements,Intersection of two arrays
5. Hash table
5.1 overview of hash table
Hash table (Hash table, also known as Hash table) is accessed directly according to the key value data structure . That is, it accesses records by mapping key values to a location in the table to speed up the search. This mapping function is called Hash function , storage of records array be called Hash table.
5.2 general operation of hash table
| method | effect |
|---|---|
| hashFunc(str,size) | Hashing strings or numbers |
| put(key,value) | Add or update an element to the hash table |
| remove(key) | Remove an element from the hash table |
| get(key) | Query a value in the hash table |
| isEmpty() | Determine whether the hash table is empty |
5.3 encapsulating hash table with js
function HashTable(limit){
this.storage = []
this.count = 0
this.limit = limit
}
// hash function
HashTable.prototype.hashFunc = function(str, size){
let hashCode = 0
//Horner algorithm
for(let i=0;i< str.length;i++){
hashCode = hashCode * 37 + str.charCodeAt(i)
}
// Remainder & & bit operation
let index = hashCode % size
return index;
}
HashTable.prototype.put =function(key, value){
let index = this.hashFunc(key, this.limit)
if(!this.storage[index]){
this.storage[index] = []
}
// Judge whether to modify data
for (let i = 0;i < this.storage[index].length; i++){
let tuple = this.storage[index][i]
if(tuple[0] == key){
tuple[1] = value
return
}
}
// Add operation
this.storage[index].push([key,value])
this.count ++
}
HashTable.prototype.get = function(key){
// 1. Get the corresponding index according to the key
let index = this.hashFunc(key, this.limit)
// 2. Get the corresponding bucket according to the index
let bucket = this.storage[index]
// 3. Linear lookup value
if(!bucket){
return null
}
for(let i=0;i<bucket.length;i++){
let tuple = bucket[i]
if(tuple[0] === key){
return tuple[1]
}
}
// 4. If none is found, null is returned
return null
}
HashTable.prototype.remove = function(key){
let index = this.hashFunc(key, this.limit),
bucket = this.storage[index]
if(!bucket){
return null
}
for (let i = 0; i< bucket.length; i++) {
let tuple = bucket[i];
if(tuple[0] == key){
bucket.splice(i,1)
this.count --
return tuple[1]
}
}
return null
}
HashTable.prototype.isEmpty = function(){
return this.count == 0
}
5.4 application of hash table
Sum of four numbers,No duplicate digit longest string,Minimum coverage string,Alphabetic word grouping
6. Binary search tree
6.1 overview of binary tree
Binary tree is an important type of tree structure. The data structure abstracted from many practical problems is often in the form of binary tree. Even a general tree can be simply transformed into binary tree, and the storage structure and algorithm of binary tree are relatively simple, so binary tree is particularly important. The characteristic of binary tree is that each node can only have two subtrees at most, which can be divided into left and right.
6.2 general operation of binary tree
| method | effect |
|---|---|
| insert(key) | Insert a new value into the tree |
| search(key) | Find a key in the tree, and return true if the node exists; If it does not exist, false is returned |
| inOrderTraverse() | Traverse all nodes through the medium order traversal method |
| preOrderTraverse() | Traverse all nodes by pre order traversal |
| postOrderTraverse() | Traverse all nodes through post order traversal |
| min() | Returns the smallest value in the tree |
| max() | Returns the largest value in the tree |
| remove(key) | Remove a value from the tree |
6.3 encapsulating binary tree with js
function BinarySearchTree(){
this.root = null
}
function CreateNode(key){
this.left = null
this.right = null
this.key = key
}
BinarySearchTree.prototype.insert = function(key){
// 1. Create node
let node = new CreateNode(key)
// 2. Judge whether the root node has a value
if(this.root === null){
this.root = node
}else{
insertNode(this.root,node)
}
function insertNode(root, node){
if(node.key < root.key){
if(!root.left){
root.left = node
}else{
insertNode(root.left, node)
}
}else {
if(!root.right){
root.right = node
}else {
insertNode(root.right, node)
}
}
}
}
BinarySearchTree.prototype.inOrderTraverse = function(node){
if(!node) return
console.log(node.key)
this.inOrderTraverse(node.left)
this.inOrderTraverse(node.right)
}
BinarySearchTree.prototype.midOrderTraverse = function(node){
if(!node) return
this.midOrderTraverse(node.left)
console.log(node.key)
this.midOrderTraverse(node.right)
}
BinarySearchTree.prototype.postOrderTraverse = function(node){
if(!node) return
this.postOrderTraverse(node.left)
this.postOrderTraverse(node.right)
console.log(node.key)
}
BinarySearchTree.prototype.max = function(){
let node = this.root
while(node !== null && node.right){
node = node.right
}
return node.key
}
BinarySearchTree.prototype.min = function(){
let node = this.root
while(node !== null && node.left !== null){
node = node.left
}
return node.key
}
BinarySearchTree.prototype.search = function(key){
let node = this.root
while(node !== null){
if(key < node.key){
node = node.left
}else if(key > node.key){
node = node.right
}else{
return true
}
}
return false
}
BinarySearchTree.prototype.remove = function(key){
let current = this.root,
parent = null,
isLeftChild = true;
// Find this node
while(current.key !== key){
parent = current
if(key < current.key){
isLeftChild = true
current = current.left
}else{
isLeftChild = false
current = current.right
}
// I didn't find it after traversal
if(current === null) return false
}
// The deleted node is a leaf node (no child nodes)
if(current.left === null && current.right === null){
if(current === this.root){
this.roo = null
}else if(isLeftChild){
parent.left = null
}else{
parent.right = null
}
}
// The deleted node has a child node
else if(current.right === null){
if(this.root === current){
this.root = current.left
}else if(isLeftChild){
parent.left = current.left
}else{
parent.right = current.left
}
}else if(current.left === null){
if(current == this.root){
this.root = current.left
}else if(isLeftChild){
parent.left = current.right
}else{
parent.right = current.right
}
}
// The deleted node has two child nodes
else{
let successor = getSuccessor(current);
if(this.root === current){
this.root = successor
}else if(isLeftChild){
parent.left = successor
}else{
parent.right = successor
}
successor.left = current.left
function getSuccessor(delNode){
let successerParent = delNode,
successer = delNode,
current = delNode.right;
while(current !== null){
successerParent = successer
successer = current
current =current.left
}
if(successer != delNode.right){
successerParent.left = successer.right
successer.right = delNode.right
}
}
return true
}
return false
}
6.4 application of binary tree
Convert binary tree into cumulative tree,Balance the binary search tree,Maximum key sum of binary search tree
7. Red black tree
7.1 overview of red black tree
Red black tree is also a self balanced binary search tree. In the red black tree, each node follows the following rules:
- Each node is either red or black
- The root node of the tree is black
- All leaf nodes are black
- If a node is red, its two child nodes are black
- There cannot be two adjacent red nodes
- All paths from a given node to its descendants contain the same number of black nodes
8. Figure
8.1 overview of drawings
Graph is an abstract model of network structure. The main purpose of research is the relationship between things. The vertex represents things and the edge represents the relationship between two things.
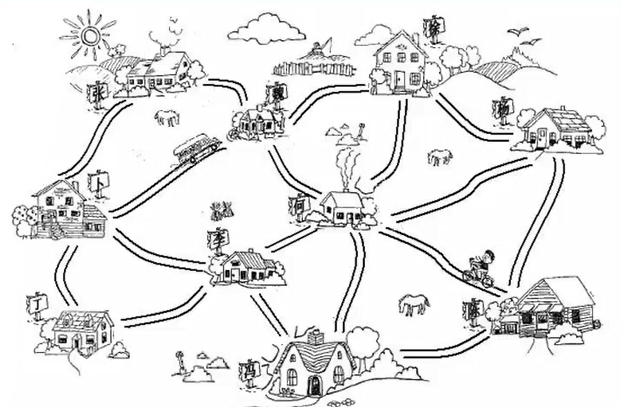
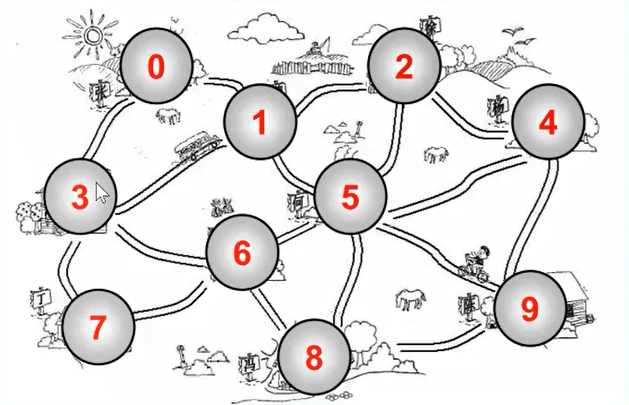
- Vertex: a node in the graph, such as a village in the graph
- Edge: the line between vertices. As shown in the figure, 0-1 has an edge, 1-2 has an edge, and 0-2 has no edge
- Adjacent vertex: the vertex with one edge connected together is called adjacent vertex, as shown in Figure 0-1 is adjacent, 0-2 is not adjacent
- Degree: the degree of a vertex is the number of adjacent vertices. As shown in figure 0, the number of vertices is 2
- Path: a path is a continuous sequence of vertices v1,v2,v3... vn
8.2 routine operation of drawing
| method | effect |
|---|---|
| addVertex(v) | add vertex |
| addEdge(v1,v2) | Add edge |
| toString() | |
| bfs() | Breadth traversal graph |
| dfs() | Depth traversal graph |
8.3 js packaging diagram
function Graph() {
//Attributes: vertices, edges
this.vertexes = []
this.edges = new Dictionay()
}
// add vertex
Graph.prototype.addVertex = function(v){
this.vertexes.push(v)
this.edges.set(v, [])
}
// Add edge
Graph.prototype.addEdge = function (v1,v2){
this.edges.get(v1).push(v2)
this.edges.get(v2).push(v1)
}
Graph.prototype.toString = function (){
let res = ''
for(let i=0;i< this.vertexes.length; i++){
res += this.vertexes[i] + '--->'
let vEdges = this.edges.get(this.vertexes[i])
for(let j=0;j < vEdges;j++){
res += vEdges
}
}
return res
}