published: true
date: 2022-1-22
tags: 'algorithm and data structure'

array

This chapter mainly introduces the basic concept and extension of array, and the storage decoupling of special matrices of two-dimensional array: symmetric matrix, triangular matrix, sparse matrix, cross linked list, etc; Then the fast transpose algorithm of sparse matrix is introduced and implemented.

Can be reproduced, but please state the source link: article source link justin3go.com (some latex formulas cannot be rendered on some platforms. You can view this website.)

array

characteristic:

• Structural fixation
• The elements in each dimension are isomorphic

Array operation:

• Access the corresponding data element at a given location.
• Modify the value of the data element at a given location.
• Arrays are generally not added or deleted.

Array sequential storage:

• Row order is the main order.

L o c ( a i j ) = L o c ( a 00 ) + ( i × n + j ) × L Loc(a_{ij}) = Loc(a_{00}) + (i\times n + j)\times L Loc(aij​)=Loc(a00​)+(i×n+j)×L

• Column order is the main order.

L o c ( a i j ) = L o c ( a 00 ) + ( j × m + i ) × L Loc(a_{ij}) = Loc(a_{00}) + (j\times m + i)\times L Loc(aij​)=Loc(a00​)+(j×m+i)×L

Special matrix

symmetric matrix

n = { i ( i + 1 ) / 2 + j , i > = j j ( j + 1 ) / 2 + i , i < j n = \begin{cases} & \text i(i+1)/2+j, i>=j \\ & \text j(j+1)/2+i, i<j \end{cases} n={​i(i+1)/2+j,i>=jj(j+1)/2+i,i<j​

Triangular matrix

n = { i ( i + 1 ) / 2 + j , i > = j n ( n + 1 ) 2 , i < j n = \begin{cases} & \text i(i+1)/2 + j, i>=j \\ & \text n(n+1)2, i<j \end{cases} n={​i(i+1)/2+j,i>=jn(n+1)2,i<j​

Tridiagonal matrix

(take the main line order as an example)

• Total length: 3n-2
• Known K (0 < = k < = 3n-3)
• i = (k+1)/3
• j = (k+1)%3+i-1

sparse matrix

definition

• Number of non-zero elements < < number of zero elements
• Irregular distribution
• For matrix M:
  • Density = total number of non-zero elements in M / total number of elements in M.
  • When density < = 5%, M is called sparse matrix.
  • Density is called the density of M.

Compressed storage

• Triple method
• Stores row, column subscripts and their values for non-zero elements.
• Store the row and column dimensions of the matrix.
• Triples: {0, 1, 12}, {0, 2, 9}, {3, 1, - 3}······
• Determinant dimension: (6, 7)
• Number of non-zero elements: 8

0	6	7	8
1	1	2	12
2	1	3	9
3	3	1	-3
4	3	6	14
5	4	3	24
6	5	2	18
7	6	1	15
8	6	4	-7

Fast transpose

General matrix transpose:

for(col = 0; col < n; col++){
    for(row = 0; row < m; row++){
        n[col][row] = m[row][col];
    }
}
//Time complexity: T(n) = O(mxn)

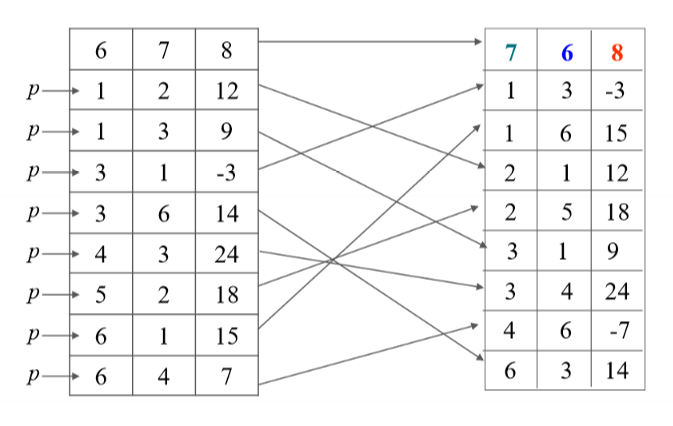
Quick transpose:

• Transpose in the order of triples in M, and put the transposed result in the appropriate position in N.
• Determine the position of the first non-zero element of each column in M in N.
  • To determine these positions, first calculate the number of non-zero elements in each column in M.
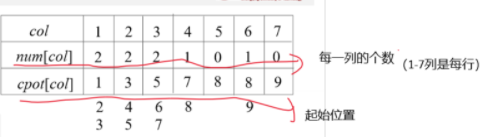
• Set two auxiliary arrays
  • num[col]: indicates the number of non-zero elements in col column in M.
  • cpot[col]: indicates the position of the first non-zero element in col column in M in N.
• Obviously
  • cpot[1] = 1
  • cpot[col] = cpot[col-1] + num[col-1]; (2<=col<=M[0])

get ready:

#include<iostream>
#include<vector>
#include<cstring>

using namespace std;

int num[5][5] = {
    {1,1,1,1,1},
    {0,0,0,1,0},
    {0,0,1,0,0},
    {0,1,0,0,0},
    {1,1,1,1,1},
};

Chained storage:

struct elements
{
    int col;
    int row;
    int val;
    elements* next;
    elements(int col, int row, int val):
    col(col),row(row),val(val),next(NULL){}
};
//If you are lazy here, you won't pass in the length. O(∩∩), the global variable defined by the array
void num2elements(elements* head){
    elements* temp = NULL;
    for(int i = 4; i >= 0; i--){
        for(int j = 4; j >= 0; j--){
            if(num[i][j] != 0){
                temp = new elements(i, j, num[i][j]);
                temp->next = head->next;
                head->next = temp;
            }
        }
    }
}

CIS storage:

vector<vector<int>> elements;
vector<int> temp;
void num2elements(){//Convert 3 tuples
    temp.push_back(5);
    temp.push_back(5);
    temp.push_back(13);
    elements.push_back(temp);
    temp.clear();
    for(int i = 0; i < 5; i++){
        for(int j = 0; j < 5; j++){
            if(num[i][j] != 0){
                temp.push_back(i);
                temp.push_back(j);
                temp.push_back(num[i][j]);
                elements.push_back(temp);
                temp.clear();
            }
        }
    }
}

Transpose operation:

int count[5];
int cpot[5];

int result[14][3];//Results after transposition;

void trans(){
    //init count
    for(int i = 0; i < elements.size(); i++){
        count[elements[i][1]]++;
    }
    //init cpot
    int sum = 0;
    for(int i = 0; i < 5; i++){
        cpot[i] = sum;
        sum += count[i];
    }
    int index = 0;
    for(int i = 1; i < 14; i++){
        index = ++cpot[elements[i][1]];

        result[index][0] = elements[i][1];
        result[index][1] = elements[i][0];
        result[index][2] = elements[i][2];
    }
    //Assign values to rows and columns and non-zero numbers
    result[0][0] = elements[0][1];
    result[0][1] = elements[0][0];
    result[0][2] = elements[0][2];
}

int T_num[5][5];
void print_result(){
    memset(T_num, 0, sizeof(T_num));
    for(int i = 1; i < 14; i++){
        T_num[result[i][0]][result[i][1]] = result[i][2];
    }
    for(int i = 0; i < 5; i++){
        for(int j = 0;j < 5; j++){
            cout << T_num[i][j] << ", ";
        }
        cout << endl;
    }
}

Main function:

int main(){
    //elements* head = new elements(5, 5, 13);
    //num2elements(head);
    num2elements();
    for(int i = 0; i < elements.size(); i++){
        for(int j = 0; j < 3; j++){
            cout << elements[i][j] << ", ";
        }
        cout << endl;
    }
    cout << "*************************" << endl;
    trans();
    for(int i = 0; i < 14; i++){
        for(int j = 0; j < 3; j++){
            cout << result[i][j] << ", ";
        }
        cout << endl;
    }
    cout << "*************************" << endl;
    print_result();
    return 0;
}

result:

/*
5, 5, 13, 
0, 0, 1,
0, 1, 1,
0, 2, 1,
0, 3, 1,
0, 4, 1,
1, 3, 1,
2, 2, 1,
3, 1, 1,
4, 0, 1,
4, 1, 1,
4, 2, 1,
4, 3, 1,
4, 4, 1, 
*************************
5, 5, 13,
0, 0, 1,
0, 4, 1,
1, 0, 1,
1, 3, 1,
1, 4, 1,
2, 0, 1,
2, 2, 1,
2, 4, 1,
3, 0, 1,
3, 1, 1,
3, 4, 1,
4, 0, 1,
4, 4, 1,
*/

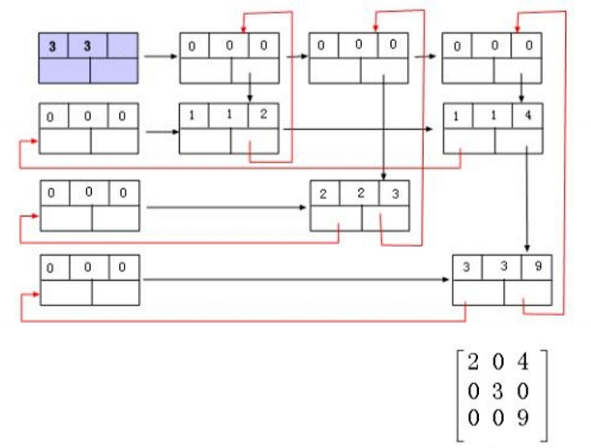
Orthogonal list

Cause: triplet table element moved

• For sequentially stored triple tables, the time overhead of moving elements is large
• In order to maintain the main row order and column order, more overhead may be incurred

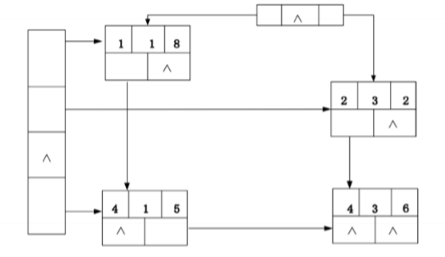
Cross linked list is another storage strategy of sparse matrix

• Each non-zero element is a node, and each node contains five fields.
  • Among them, row field i, column field j and value field v represent row subscript, column subscript and value of non-zero elements respectively.
  • The right field right links the next non-zero element in the same row.
  • The down field down links the next non-zero element in the same column.
• Cross linked list storage requires additional pointer fields, row and column pointers
  • Generally, when the number of non-zero elements does not exceed 20% of the total number of elements, it is suitable for cross linked list storage.