6, Levinstein edit distance

The previous several distance calculation methods are for words with the same length. Levinstein edit distance can calculate the distance between two words with different lengths; Levinstein edit distance is the minimum number of edits required to add, delete, or replace one character with another;

Assuming that the lengths of two words u and v are i and j respectively, they can be calculated in the following cases

When the length of a word is 0, edit the length of the word whose distance is not zero;

From the definition of editing distance, in the process of word change, the change of each character can be regarded as the deletion, addition and replacement of the current character based on the editing distance of its prefix substring;

name when the length of u and v is not 0, there are three possibilities of conversion

If the prefix of u that does not contain the last character is converted to v, this is the case of deleting the character;

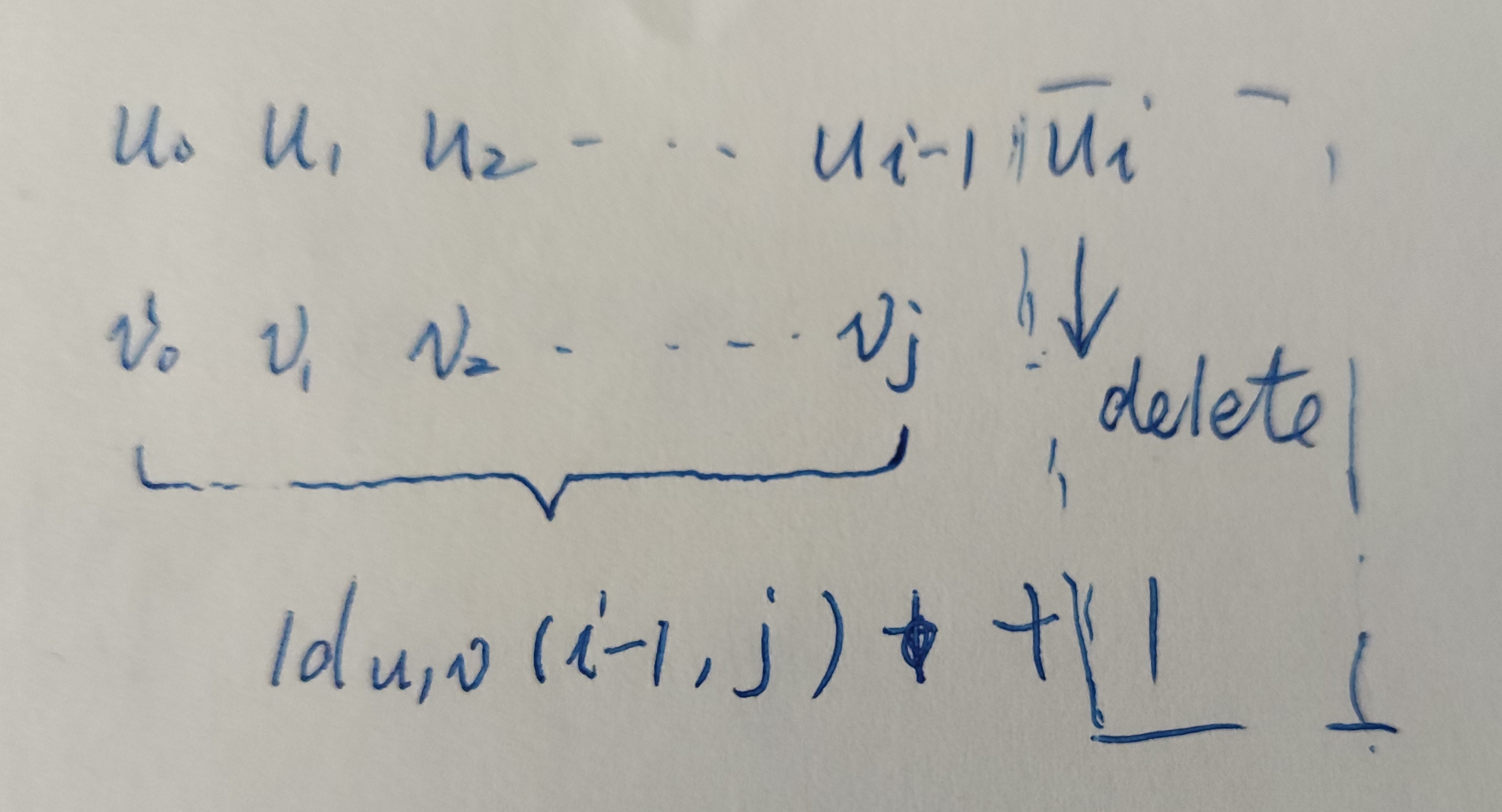
The mathematical formula is

u has been completely converted to v, which is the case of adding characters on the premise that it does not contain the prefix of the last character;

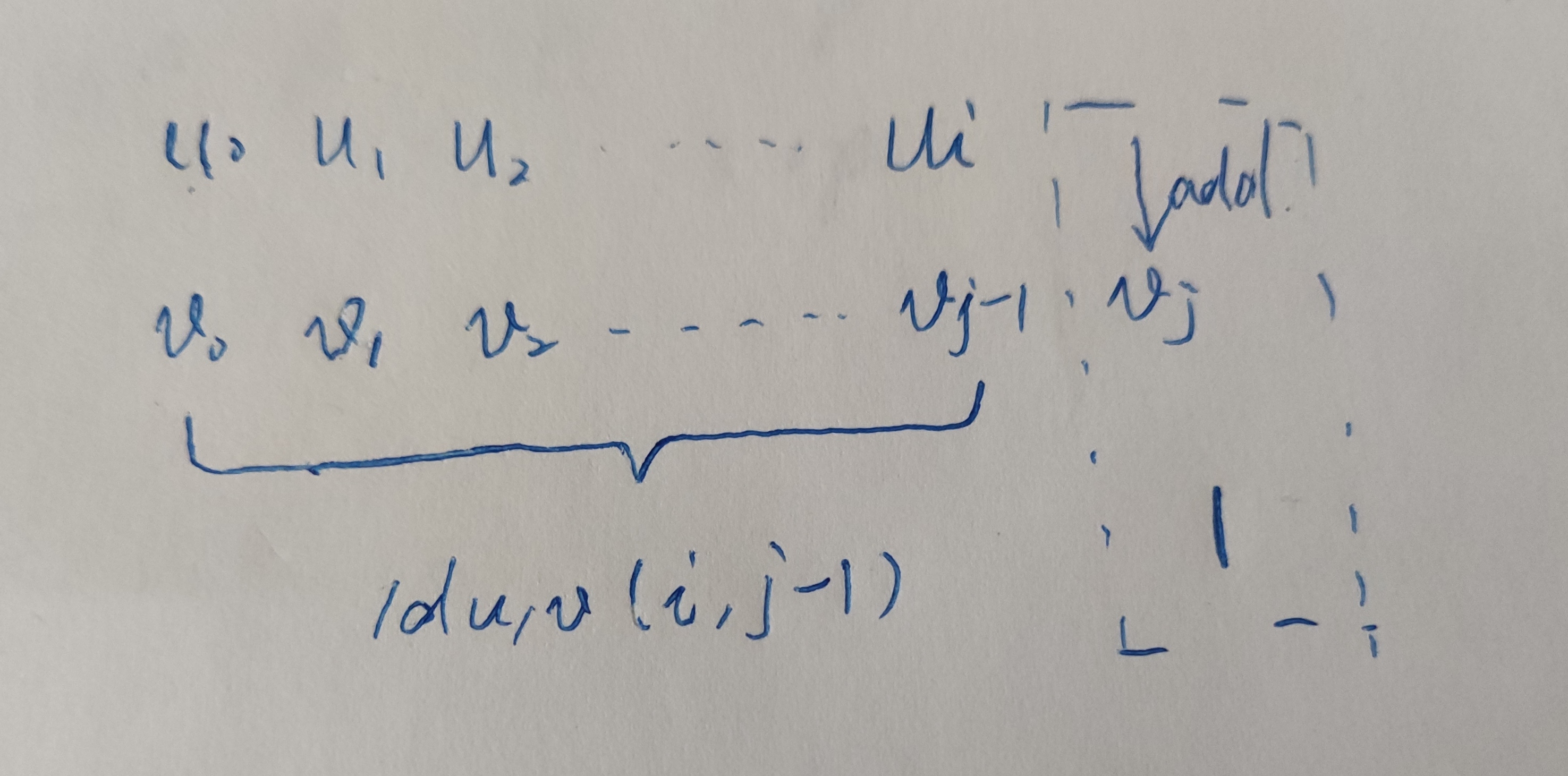
The mathematical formula is

On the premise that the u prefix has been converted to the v prefix, it needs to be replaced according to whether the last character of the two words is equal or not;

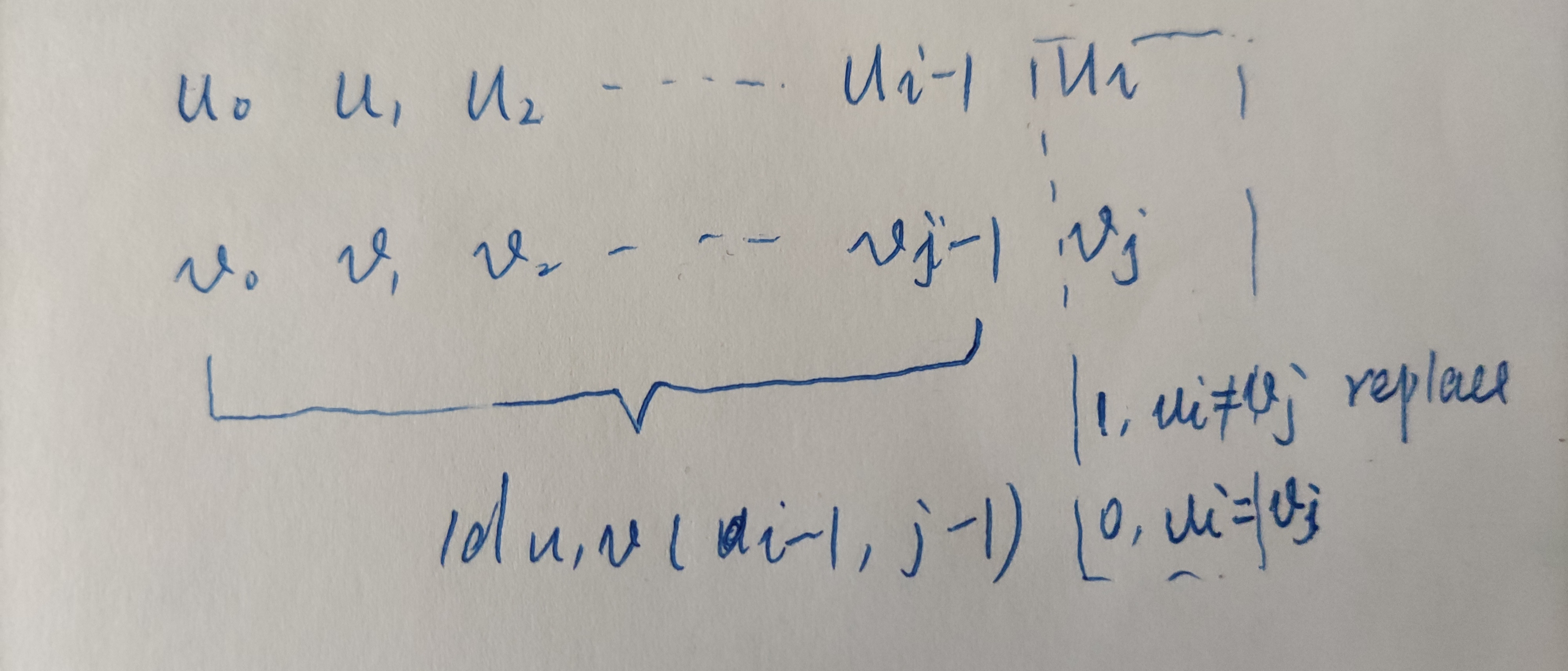
The mathematical formula is

Then take the smallest value in the three cases as the editing distance;

The above are abstract descriptions from the perspective of recursion, which may be a little difficult to understand directly; Let's take the transformation from vlna to vlan as an example and use the matrix to intuitively understand the algorithm;

The first row of the matrix can be understood as the prefix substring of vlna, which is transformed into the editing distance of v;

V = > V, edit distance is 0;

VL = > V, editing distance is 1;

In the same way, the first column of the matrix is the edit distance from the substring v of vlna to all prefix substrings of vlan;

Next, we can see how the edit distance of the second row and the second column is calculated;

The first column in the second row indicates that the editing distance of V = > VL is 1, i.e

At this time, you only need to delete l on this basis; This is the case of corresponding deleted characters. At this time, the editing distance is 2;

The first row and the second column indicate that the editing distance of VL = > V is 1, i.e

At this time, you only need to add the character l on this basis; This is the case corresponding to the newly added characters. At this time, the editing distance is 2;

The first row and the first column indicate that the editing distance of V = > V is 0, i.e

Since the characters in both words are l, the characters do not need to be replaced. This is the case of corresponding character replacement. At this time, the editing distance is 0;

Through the above analysis, we can know that the editing distance is 0; At the same time, we can also find that the editing distance of each position in the matrix is related to the editing distance of its left, upper left and upper. We only need to calculate the smallest of the three as the editing distance;

Through the above edit distance matrix, we finally only focus on the value of the last cell, and its calculation only needs to focus on the edit distance between the previous row and the current row;

For the convenience of calculation, we can add a blank placeholder in front of u and v respectively, so that there are editing distances in three directions for each character;

We use the following method to calculate the edit distance and edit distance matrix;

import copy
import pandas as pd

def levenshtein_edit_distance(u, v):
    u = u.lower()
    v = v.lower()
    distance = 0

    if len(u) == 0:
        distance = len(v)
    elif len(v) == 0:
        distance = len(u)
    else:
        edit_matrix = []
        pre_row = [0] * (len(v) + 1)
        current_row = [0] * (len(v) + 1)

        # Initializes the edit distance of the padding line
        for i in range(len(u) +1):
            pre_row[i] = i

        for i in range(len(u)):
            current_row[0] = i + 1
            for j in range(len(v)):
                cost = 0 if u[i] == v[j] else 1
                current_row[j+1] = min(current_row[j] + 1, pre_row[j+1] + 1, pre_row[j] + cost)

            for j in range(len(pre_row)):
                pre_row[j] = current_row[j]

            edit_matrix.append(copy.copy(current_row))

        distance = current_row[len(v)]
        edit_matrix = np.array(edit_matrix)
        edit_matrix = edit_matrix.T
        edit_matrix = edit_matrix[1:,]
        edit_matrix = pd.DataFrame(data = edit_matrix, index=list(v), columns=list(u))

    return distance,edit_matrix

We use the same keywords and use the following code to test

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]


input_word = 'vlna'
for word in words:
    distance, martrix = levenshtein_edit_distance(input_word, word)
    print(f"{input_word} and {word} levenshtein edit distance is  {distance}")
    print('the complate edit distance matrix')
    print(martrix)
    

vlna and vlan levenshtein edit distance is  2
the complate edit distance matrix
   v  l  n  a
v  0  1  2  3
l  1  0  1  2
a  2  1  1  1
n  3  2  1  2
vlna and vlna levenshtein edit distance is  0
the complate edit distance matrix
   v  l  n  a
v  0  1  2  3
l  1  0  1  2
n  2  1  0  1
a  3  2  1  0
vlna and http levenshtein edit distance is  4
the complate edit distance matrix
   v  l  n  a
h  1  2  3  4
t  2  2  3  4
t  3  3  3  4
p  4  4  4  4

7, Cosine distance

Cosine distance is a concept associated with cosine similarity; We can use vectors to represent different words, and the cosine value between two different word vectors is the cosine similarity; The smaller the angle between the two, the smaller the cosine value, and the two are approximately similar;

According to the inner product formula of the vector, the following cosine similarity formula can be obtained;

The greater the cosine similarity, the more similar the two words are, and the distance is just the opposite, so the cosine distance is

To calculate the cosine distance, we need to first convert the word into a vector. We can use SciPy stats. Itemfreq to vectorize words in character bag; We calculate the number of occurrences of each character in each word by the following method;

from scipy.stats import itemfreq

def boc_term_vectors(words):
    words = [word.lower() for word in words]
    unique_chars = np.unique(np.hstack([list(word) for word in words]))
    word_term_counts = [{char:count for char,count in itemfreq(list(word))} for word in words]


    boc_vectors = [np.array([
        int(word_term_count.get(char, 0)) for char in unique_chars])
        for   word_term_count in  word_term_counts
    ]

    return list(unique_chars), boc_vectors

Test it with the following code

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]

chars, (boc_vlan,boc_vlna,boc_http) = boc_term_vectors(words)
print(f'all chars {chars}')
print(f"vlan {boc_vlan}")
print(f"vlna {boc_vlna}")
print(f"http {boc_http}")


all chars ['a', 'h', 'l', 'n', 'p', 't', 'v']
vlan [1 0 1 1 0 0 1]
vlna [1 0 1 1 0 0 1]
http [0 1 0 0 1 2 0]

We can use the following method to calculate the cosine distance according to the formula;

def cosin_distance(u, v):
    distance = 1.0 - np.dot(u,v)/(np.sqrt(sum(np.square(u))) * np.sqrt(sum(np.square(v))))
    return distance

Using the same keyword, test the cosine distance with the following code;

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]

chars, boc_words = boc_term_vectors(words)
input_word =vlna
boc_input = boc_words[1]
for word, boc_word in zip(words, boc_words):
    print(f'{input_word} and {word} cosine distance id {cosin_distance(boc_input, boc_word)}')
    

vlna and vlan cosine distance id 0.0
vlna and vlna cosine distance id 0.0
vlna and http cosine distance id 1.0