📚 Reference book: data structure (C language) - edited by Yan Weimin, Tsinghua University Press.

📖 chart

Graph is a more complex data structure than linear table and tree. In the graph structure, the relationship between nodes can be arbitrary, and any two data elements in the graph can be related to each other.
The most representative graph in life is the map we use. Each city represents a vertex. There are various relationships between cities, and the graph can be divided into directed graph and undirected graph, as follows:

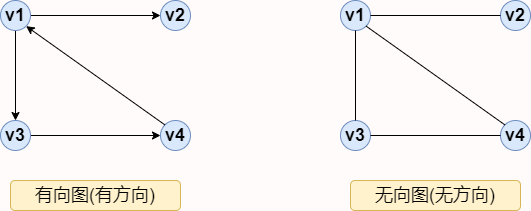
Terms related to drawings:
♥ Vertex: the data elements in the graph are called vertices;
♥ Arc:

• In a directed graph, V1 to V2 are called an arc: < V1, V2 >;
• In an undirected graph, V1 to V2 are called an edge: (v1,v2);

♥ Arc tail: v1 is called arc tail (or initial point);
♥ Arc head: v2 is called arc head (or terminal point);
♥ Complete graph: Yes 1 2 n ( n − 1 ) \bf\color{teal}\dfrac{1}{2}n\left( n-1\right) An undirected graph with 21 n(n − 1) edges is called a complete graph;
♥ Directed complete graph: n ( n − 1 ) \bf\color{teal}n\left( n-1\right) A directed graph with n(n − 1) arcs is called a directed complete graph;
♥ Sparse graph: having few edges or arcs (e.g e < n log ⁡ n \bf\color{teal}e<n\log{n} E < nlogn) is called sparse graph;
♥ Dense graph: sparse graph; otherwise, it is dense graph;
♥ Weight: sometimes the edge or arc of a graph has a number related to it. The number related to the edge or arc of this graph is called weight;
♥ Net: the graph with weight is called net;
♥ Degree of vertex: refers to the number of edges connected to the vertex. As above, the degree of vertex V1 of undirected graph is: 3
♥ Vertex exit: refers to the number of edges with this vertex as the tail. As above, the exit of vertex V1 of digraph is: 2
♥ Vertex penetration: refers to the number of edges with this vertex as the head. The penetration of vertex V1 of the above directed graph is: 1

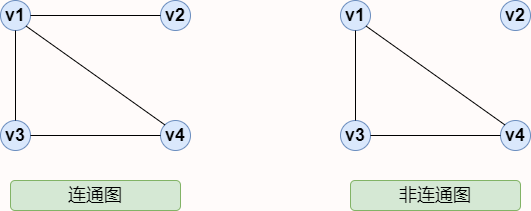
😄 In an undirected graph, if any two vertices are connected, it is called a connected graph (undirected graph). Unconnected graph and connected graph are distinguished as follows:

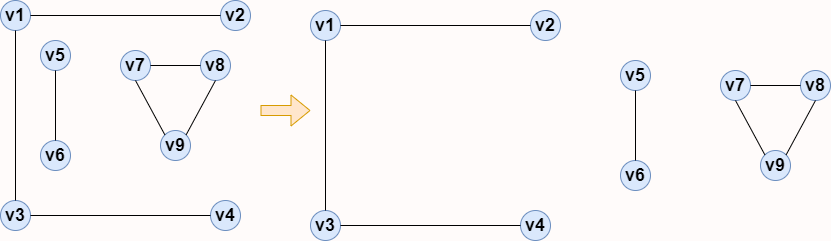
♥ Connected component: refers to the polar connected subgraph in an undirected graph. As follows, a non connected graph has three connected components:

😄 In a directed graph, for each pair of vi, vj (vi! = vj), there is a path force from vi to vj and vj to vi, which is called a strongly connected graph (directed graph), and the maximal strongly connected subgraph in a directed graph is called the strongly connected component of a directed graph.

🍵 Spanning tree: the spanning tree of a connected graph is a minimal connected subgraph, which contains all vertices, but only enough n-1 edges to form a tree.

🌔 a key:
🍊 A spanning tree with n vertices has only n-1 edges.
🍊 If there are more than n-1 edges, it must form a ring (loop).
🍊 A graph with n-1 edges is not necessarily a spanning tree.
🍊 A graph is unconnected if it has n vertices and less than n-1 edges

📖 Storage structure of graph

🍋 Array representation of graphs (adjacency matrix representation)

#define INFINITY 	 INT_MAX 	// Maximum ∞
#define MAX_VERTEX_NUM 20 / / maximum number of vertices
typedef enum {DG,DN,UDG,UDN} GraphKind; //Directed graph, directed net, undirected graph, undirected net
typedef struct ArcCell {
	VRType adj;	//VRType is a vertex relationship type. More than weighted graphs are represented by 1 or 0, indicating whether they are adjacent or not. For weighted graphs, it is a weight
	InfoType *info; //Pointer to the arc related information
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct {
	VertexType vexs[MAX_VERTEX_NUM];	//Vertex vector
	AdjMatrix arcs;	//adjacency matrix 
	int vexnum, arcnum;	//Current vertices and arcs
	GraphKind kind;	//Types of Graphs
}MGraph;

🍋 Adjacency matrix (array) represents the advantages of graph:
🍎 Intuitive, simple and easy to understand;
🍎 It is convenient to check whether any pair of vertices have edges;
🍎 It is convenient to find all "adjacency points" of any vertex;
🍎 It is convenient to calculate the degree of any vertex;

🍋 The adjacency matrix (array) represents the disadvantages of the graph:
🍎 Inconvenient to add and delete vertices;
🍎 Waste of space - there are a large number of 0 elements in sparse graphs;
🍎 Waste of time -- count the total number of edges of a sparse graph;

🔗 Relevant codes:

#include "stdio.h"
#include "stdlib.h"
#define TRUE     1
#define FALSE    0
#define OK       1
#define ERROR    0
#define OVERFLOW -2
#define INFINITY INT_MAX 	// Maximum 
#define MAX_VERTEX_NUM 20 	// max vertex  

typedef int Status;
typedef int VertexType;
typedef int ArcType;
typedef struct {
	VertexType	vexs[MAX_VERTEX_NUM];				//Vertex vector
	ArcType	arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];	//adjacency matrix 
	int vexnum,arcnum;		//Current vertex number and arc number of graph
} MGraph;

Status LocateVex(MGraph G,VertexType v);
//Position v in adjacency matrix
Status LocateVex(MGraph G,VertexType v) {
	int i;
	for(i=0; i<G.vexnum; i++) {
		if(G.vexs[i]==v) return i;
	}
	return -1;
}

Status CreateUDGraph(MGraph &G);
//Constructing undirected graph UDG represented by adjacency matrix
Status CreateUDGraph(MGraph &G) {
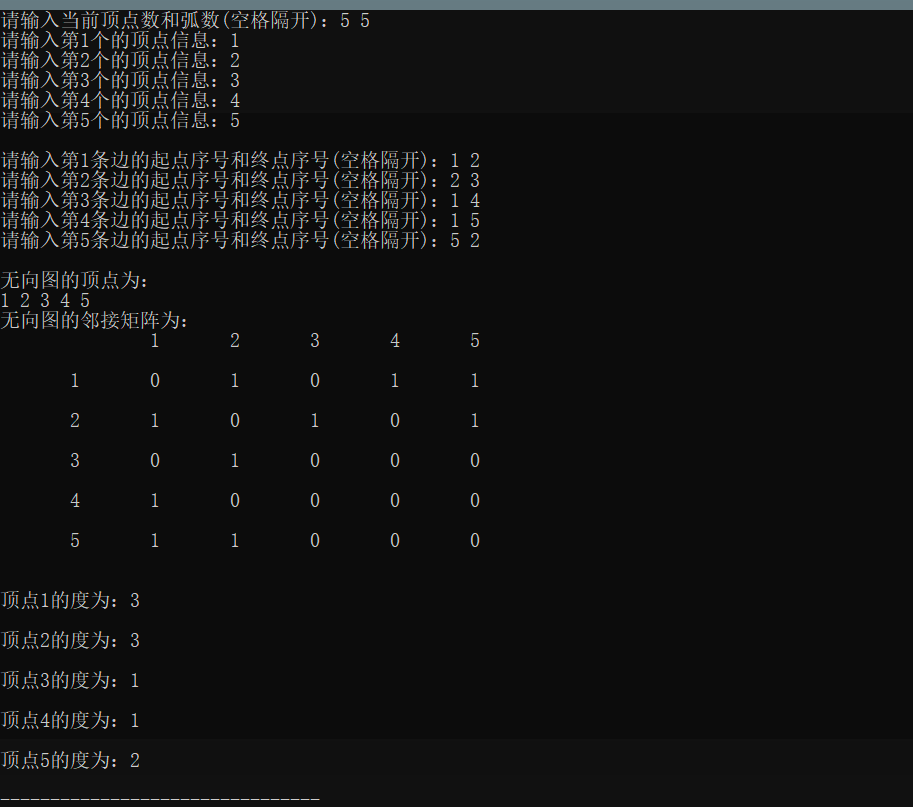
	printf("Please enter the current number of vertices and arcs(Space separated): ");
	scanf("%d %d",&G.vexnum,&G.arcnum);
	int i,j,k;
	int v1,v2;	//Arc tail and arc head 
	for(i=0; i<G.vexnum; i++) {
		printf("Please enter page%d Vertex information for:",i+1);
		scanf("%d",&G.vexs[i]);
	}
	printf("\n");
	for(i=0; i<G.vexnum; i++) 	//Initialize adjacency matrix
		for(j=0; j<G.vexnum; j++) {
			G.arcs[i][j]= {INFINITY};	
		}
	for(k=0; k<G.arcnum; k++) {
		printf("Please enter page%d Start sequence number and end sequence number of the edge(Space separated): ",k+1);
		scanf("%d %d",&v1,&v2);
		i=LocateVex(G,v1);
		j=LocateVex(G,v2);
		if(i==-1 || j==-1) return ERROR;
		else {
			G.arcs[i][j]=1;
			G.arcs[j][i]=1;
		}
	}
	return OK;
}

Status PrintUDGraph(MGraph G);
//Print map
Status PrintUDGraph(MGraph G) {
	int i,j;
	printf("\n The vertices of an undirected graph are:\n");
	for(i=0; i<G.vexnum; i++)
		printf("%d ",G.vexs[i]);
	printf("\n The adjacency matrix of undirected graph is:\n");
	printf("\t");
	for(i=0; i<G.vexnum; ++i)
		printf("%8d", G.vexs[i]);
	putchar('\n');
	for(i=0; i<G.vexnum; ++i) {
		printf("\n%8d", G.vexs[i]);
		for(j=0; j<G.vexnum; ++j) {
			if(G.arcs[i][j] == INT_MAX) printf("%8s", "0");
			else printf("%8d",G.arcs[i][j]);
		}
		printf("\n");
	}
	return OK;
}

Status Degree(MGraph G);
//Finding the degree of each vertex of undirected graph
Status Degree(MGraph G) {
	int i,j, deg;
	for(i=0; i<G.vexnum; i++) {
		deg=0;	//Initial 0
		for(j=0; j<G.vexnum; j++) {
			if(G.arcs[i][j]  != INT_MAX) {
				deg++;
			}
		}
		if(deg == 0)  printf("\n vertex%d No degree\n",G.vexs[i]);
		else printf("\n vertex%d The degree of is:%d\n",G.vexs[i],deg);
	}
}

int main(void) {
	MGraph G;
	CreateUDGraph(G);
	PrintUDGraph(G);
	putchar('\n');
	Degree(G);
	return 0;
}

realization: