Title Description

Given a tree, preorder and inorder are traversed sequentially. Please construct a binary tree and return its root node.

Example 1

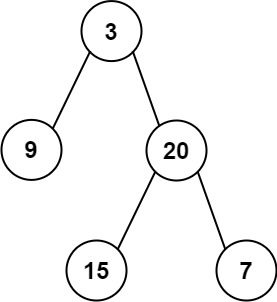
Input: preorder = [3,9,20,15,7], inorder=[9,3,15,20,7]
output:[3,9,20,null,null,15,7]

Example 2

Input: preorder=[-1], inorder=[-1]
output: [-1]

Tips

• 1 ≤ p r e o r d e r . l e n g t h ≤ 3000 1\le preorder.length \le 3000 1≤preorder.length≤3000
• i n o r d e r . l e n g t h = = p r e o r d e r . l e n g t h inorder.length == preorder.length inorder.length==preorder.length
• − 3000 ≤ p r e o r d e r [ i ] , i n o r d e r [ i ] ≤ 3000 -3000\le preorder[i], inorder[i]\le3000 −3000≤preorder[i],inorder[i]≤3000
• Neither preorder nor inorder has duplicate elements
• Inorders appear in preorder
• Preorder guarantees the sequence of preorder traversal of a binary tree
• inorder guarantees the ordered traversal sequence of a binary tree

Solving problems

This problem is solved recursively. First, for any tree, the prefix traversal always takes the form of [root node, [left subtree's prefix traversal result], [right subtree's prefix traversal result], that is, the root node is always the first node in the prefix traversal, and the intermediate traversal takes the form of [left subtree's middle traversal result], root node, [right subtree's middle traversal result].

As long as the root node is located in the middle traversal, the number of nodes in the left subtree and the right subtree can be known, respectively. Since the length of the prefix and median traversals of the same subtree are obviously the same, all the left and right parentheses in the above form can be located in the result of the prefix traversal.

In this way, you know the results of the left subtree's prefix and median traversal, and the right subtree's prefix and median traversal. Then you can construct the left subtree and the right subtree recursively, and then stitch the two subtrees to the left and right of the root node.

Note: To quickly locate the root node, a hash table is used where each key in the hash table represents an element (the value of the node) and the value represents its position in the middle traversal. During the construction of a binary tree, a hash table can be built by scanning the sequentially traversed list once. Time complexity is O(1) when searching.

Code Display

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @FileName  :BuildTree.py
# @Time      :2022/1/24 21:13
# @Author    :PangXZ
# Leetcode: 105 Construct Binary Tree from Pre-order and Medium-order Traversal Sequences

# Definition for a binary tree node.
from typing import List


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        n = len(preorder)
        # Construct a hash table to quickly locate the root node
        index_map = {element: i for i, element in enumerate(inorder)}

        # Define the Reconstructed Binary Tree Function
        def building(preorder_left: int, preorder_right: int, inorder_left: int, inorder_right: int):
            if preorder_left > preorder_right or inorder_left > inorder_right:
                return None
            # The first position in the prefix traversal is the root node
            preorder_root = preorder_left
            # Find Root Node in Ordered Traverse
            inorder_root = index_map[preorder[preorder_root]]

            # Build the root node of the binary tree first
            root = TreeNode(preorder[preorder_root])
            # Get the number of nodes in the left subtree
            size_left = inorder_root - inorder_left
            # Construct the left subtree recursively and link to the root node
            # The [size_left] elements from left boundary + 1 in a sequential traversal correspond to the elements from left boundary to root node positioning-1 in a sequential traversal
            root.left = building(preorder_left + 1, preorder_left + size_left, inorder_left, inorder_root - 1)
            # Recursively construct the right subtree and connect to the root node
            # Elements in a sequential traversal [starting with the number of left + 1 + left subtree nodes and going to the right boundary] correspond to elements in a sequential traversal [positioning + 1 from the root node, to the right boundary]
            root.right = building(preorder_left + 1 + size_left, preorder_right, inorder_root + 1, inorder_right)
            return root

        return building(0, n - 1, 0, n - 1)

Complexity analysis

• Time Complexity: O ( n ) O(n) O(n), where n is the number of nodes in the tree
• Spatial Complexity: O ( n ) O(n) O(n), in addition to requiring n spaces to return the answer, n spaces are needed to store the hash table, and O(h) (h is the height of the tree) is used to represent the stack space for recursion, where h<n, so the overall spatial complexity is O(n).