1 definition of binary sort tree:
If its left subtree is not empty, the value of all nodes on the left subtree is less than that of its root node
If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node
The left and right subtrees of the root node are binary sort trees
(binary sort tree may degenerate into a linked list, so there is the concept of balanced binary tree; the middle order traversal of binary sort tree is ordered from small to large)
2 binary sort tree structure and node creation function
typedef struct Tree //Binary tree
{
int data; //Data domain
struct Tree *left; //Left child node pointer
struct Tree *right; //Right child node pointer
} Tree;
Tree *createBinarySortTreeNode(int data)
{
Tree *node = (Tree *)malloc(sizeof(Tree));
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}3 node insertion of binary sort tree
Idea: compare the data of the node to be inserted with the data of the root node. If it is less than the data of the root node, insert the left subtree of the root node; If it is greater than the data of the root node, insert the right subtree of the root node;
Inserting a subtree is equivalent to inserting a smaller tree, so it can be implemented recursively until a node without a subtree is found, and the new node is inserted below it to become a leaf node.
void insertBinarySortTreeNode(Tree *dataNode, Tree **root) //The binary sort tree is inserted into the node. Because the root node may change, the secondary pointer is passed
{
if (*root == NULL || dataNode == NULL)
{
*root = dataNode;
return;
}
if (dataNode->data > (*root)->data)//If the inserted node is larger than the data of the original node, the inserted node needs to be placed in the right subtree of root
{
if ((*root)->right == NULL)//Find insertion location
{
(*root)->right = dataNode;
return;
}
if ((*root)->right)
insertBinarySortTreeNode(dataNode, &(*root)->right);//Recursively find the insertion position of dataNode
}
if (dataNode->data <= (*root)->data)//If the equals sign is removed, it means that nodes with the same data are not inserted
{
if ((*root)->left == NULL)//Find insertion location
{
(*root)->left = dataNode;
return;
}
if ((*root)->left)
insertBinarySortTreeNode(dataNode, &(*root)->left); //Recursively find the insertion position of dataNode
}
}4. Get the maximum key value node of binary sort tree
- Idea: since the key values of the nodes of the right subtree are greater than those of the root node of the binary sort tree, you need to start searching from the root node of the right subtree Until the right child node of the last right subtree is found, that is, the node corresponding to the maximum key value. This process can be implemented recursively.
Tree *maxValueOfBinaryTree(Tree *root)
{
if (root == NULL)//Null pointer judgment
return NULL;
Tree *pointer = root;
while (pointer->right)//After jumping out of the loop, the pointer points to the last right child node
pointer = pointer->right;
return pointer;
}5. Obtaining the minimum key value node of binary sort tree (the idea is the same as above and will not be repeated)
Tree *minValueOfBinaryTree(Tree *root)
{
if (root == NULL)
return NULL;
Tree *pointer = root;
while (pointer->left)
pointer = pointer->left;
return pointer;
}6 binary sort tree finds the parent node of the specified node
Tree *parentNodeOfBinaryTreeNode(Tree *dataNode, Tree *root) //Gets the parent node of the dataNode node
{
if (dataNode == NULL || root == NULL || root == dataNode) //Null pointer judgment, and root itself has no parent node
return NULL;
Tree *pointer = root;
Tree *parentNode = pointer;
while (pointer != NULL && pointer->data != dataNode->data)
{
parentNode = pointer;
if (dataNode->data > pointer->data)
pointer = pointer->right;
else
pointer = pointer->left;
} //After each cycle, the parentNode is always the parent node of the pointer
//After the loop jumps out, either the dataNode is found or the pointer is NULL
if (pointer == NULL)
{
printf("node dataNode non-existent\n");
return NULL;
}
return parentNode;
}7 delete node in binary sort tree
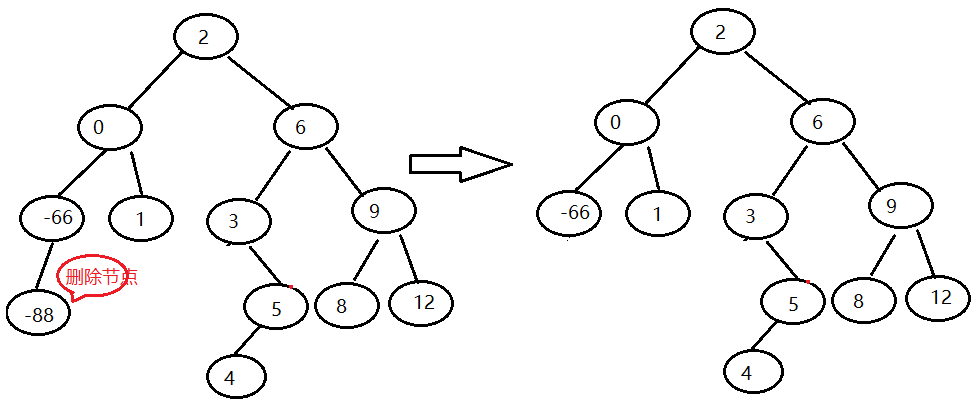
- 7.1 if the deleted node is a leaf node (no child node), set the deleted node to NULL (the parent node of the deleted node points to NULL); Special case: if the deleted node is the root node, set root to NULL
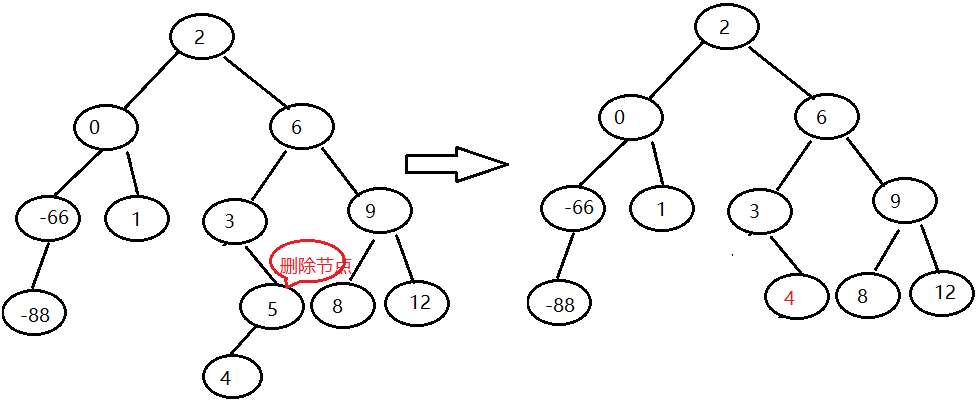
- 7.2 if the deleted node has a child node, point the parent node of the deleted node to the child node of the deleted node. Special case: if the deleted node is the root node, it can be considered to delete the head node of the linked list and take the second node as the header.
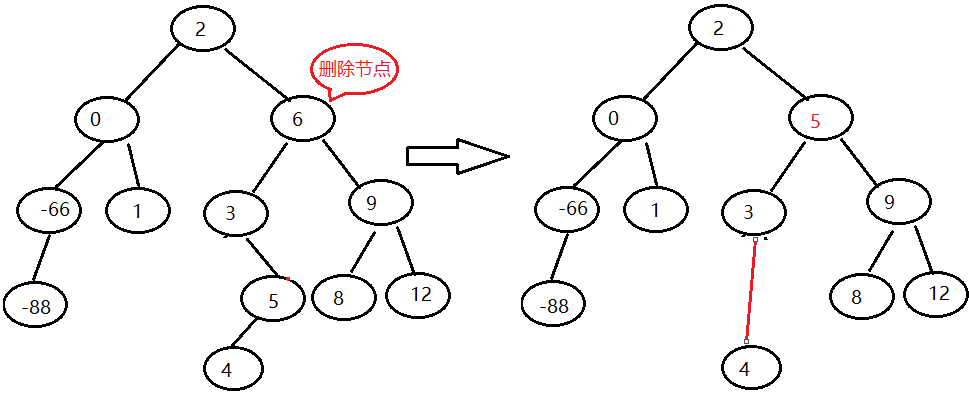
- 7.3 if the deleted node has two child nodes, in order to ensure the order of the binary sort tree, it is necessary to find the two nodes closest to the key value of the deleted node. According to the characteristics of the binary tree, these two nodes are located in the rightmost node of the left subtree and the leftmost node of the right subtree of the deleted node. Then point the parent node of the deleted node to any one of them (for example, the rightmost node of the left subtree, hereinafter referred to as the substitute node), and the right pointer of the substitute node points to the right subtree of the deleted node; If the parent node of the substitute node is not the deleted node, the left pointer of the substitute node points to the left subtree of the deleted node, and the parent node of the substitute node points to the left subtree of the substitute node (there is no left subtree when the substitute node is at the rightmost); Special case 1: when the deleted node is root, special case 2: when the parent node of the replacement node is the deleted node, the code analysis can be seen
- Finally, release the space for deleting nodes
The code is as follows
void deleteBinarySortTreeNode(Tree *deleteNode, Tree **root) //Delete a node in the binary tree
{
Tree *parentOfDeleteNode = parentNodeOfBinaryTreeNode(deleteNode, *root); //Delete parent node of node
if (deleteNode == NULL || root == NULL) //Null pointer judgment
return;
if (deleteNode != *root && parentOfDeleteNode == NULL) //If the deleted node is not root and parentOfDeleteNode==NULL, it means that the deleted node is not found or the root node of the tree is NULL, so it ends directly;
return;
if (deleteNode->left == NULL && deleteNode->right == NULL) // Case: 1 case where the deleted node is a leaf node
{
if (*root == deleteNode) //The deleted node is the root node
{
*root = NULL;
return;
}
if (parentOfDeleteNode->left == deleteNode)
parentOfDeleteNode->left = NULL;
if (parentOfDeleteNode->right == deleteNode)
parentOfDeleteNode->right = NULL;
}
else if (deleteNode->left == NULL || deleteNode->right == NULL) // case: 2 the deleted node has only one of the left subtree or the right subtree
{
if (*root == deleteNode)
{
if ((*root)->left != NULL) //The deleted node is the root node, and the root node has only the left subtree
(*root) = (*root)->left;
else if ((*root)->right != NULL)
(*root) = (*root)->right; //The deleted node is the root node, and the root node has only the right subtree
}
else if (deleteNode->left != NULL) //The deleted node has only the left subtree
{
if (parentOfDeleteNode->left == deleteNode) //The deleted node is the left child node of the parent node, and the deleted node has only the left child tree
parentOfDeleteNode->left = deleteNode->left; //Point the left of the parent node to the left child node of deleteNode
if (parentOfDeleteNode->right == deleteNode)
parentOfDeleteNode->right = deleteNode->left;
}
else if (deleteNode->right != NULL)
{
if (parentOfDeleteNode->left == deleteNode) //
parentOfDeleteNode->left = deleteNode->right;
if (parentOfDeleteNode->right == deleteNode)
parentOfDeleteNode->right = deleteNode->right;
}
}
else if (deleteNode->left != NULL || deleteNode->right != NULL) // case: 3 deleted nodes have left subtree and right subtree
{
Tree *replaceNode = maxValueOfBinaryTree(deleteNode->left);
//Find the rightmost node of the left subtree of the deleted node (corresponding to the maximum key value of the left subtree) as the substitute node. The key value of the substitute node is adjacent to the key value of the deleted node,
Tree *parentOfReplaceNode = parentNodeOfBinaryTreeNode(replaceNode, *root); //Gets the parent node of the substitute node
if (*root == deleteNode)
{
parentOfReplaceNode->right = replaceNode->left;
replaceNode->left = (*root)->left;
replaceNode->right = (*root)->right;
(*root) = replaceNode;
}
else if (parentOfDeleteNode->left == deleteNode) //The deleted node is the left child of its parent node
{
parentOfDeleteNode->left = replaceNode; //The parent node left of the deleted node points to the substitute node
replaceNode->left = deleteNode->left;
if (parentOfReplaceNode != deleteNode)
{
replaceNode->right = deleteNode->right;
//The right subtree of the substitute node points to the right subtree of the deleted node (if the parent node of the substitute node is the deleted node, deletenode - > right is the substitute node, resulting in the loss of the following subtree; parentofreplacenode - > right is meaningless)
parentOfReplaceNode->right = replaceNode->left;
}
else if (parentOfReplaceNode == deleteNode)
replaceNode->right = deleteNode->right->left; //The right subtree of the replacement node points to the left subtree of the replacement node. It is easy to understand from the tree diagram
}
else if (parentOfDeleteNode->right == deleteNode) //The deleted node is the right child node of the parent node
{
parentOfDeleteNode->right = replaceNode; //Delete the parent node of the node. right points to the node corresponding to the maximum key value of the left subtree
replaceNode->right = deleteNode->right;
if (parentOfReplaceNode != deleteNode)
{
replaceNode->left = replaceNode->left;
parentOfReplaceNode->right = replaceNode->left;
}
else if (parentOfReplaceNode == deleteNode)
replaceNode->left = replaceNode->left->left;
}
}
free(deleteNode);
}8 in order to traverse the code and find the specified node code
Tree *searchTreeNode(Tree *root, int value) //Searches for nodes in a binary sort tree that contain the specified data
{
if (root == NULL)
return NULL;
if (root->data > value)
return searchTreeNode(root->left, value);
if (root->data < value)
return searchTreeNode(root->right, value);
else
return root;
}
void inOrderList(Tree *root)//Middle order traversal
{
if (root == NULL)
return;
inOrderList(root->left);
printf("%d->", root->data);
inOrderList(root->right);
}9 function test and operation results
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main()
{
int array[] = {2, 6, 9, 8, 12, 3, 5, 4, 0, -66, 1, -88};
Tree root = {2, NULL, NULL};
Tree *pointer = &root;
for (int i = 1; i < sizeof(array) / sizeof(array[0]); i++)
{
Tree *node = createBinarySortTreeNode(array[i]);
insertBinarySortTreeNode(node, &pointer);//Insert node
}
inOrderList(&root); //Order traversal in binary sort tree
puts("");
Tree *maxNode = maxValueOfBinaryTree(&root);//Maximum key node lookup
printf("the maxValueNode:{data:%d left:%p right:%p}\n", maxNode->data, maxNode->left, maxNode->right);
Tree *minNode = minValueOfBinaryTree(&root);//Minimum key node lookup
printf("the minValueNode:{data:%d left:%p right:%p}\n", minNode->data, minNode->left, minNode->right);
Tree *searchNode = searchTreeNode(&root, 6);//Find the specified node
printf("searchNode->{data:%d left:%p right:%p}\n", searchNode->data, searchNode->left, searchNode->right);
Tree *parentNode = parentNodeOfBinaryTreeNode(searchNode, &root);//Specifies the parent node lookup for the node
printf("parentNode->{data:%d left:%p right:%p} searchNode:%p\n", parentNode->data, parentNode->left, parentNode->right, searchNode);
//If the test deletes the root node, you need to remove the data of the parent node in the uplink printf, because it is NULL and cannot be dereferenced
Tree *pointer2 = &root;
deleteBinarySortTreeNode(searchNode, &pointer2);//Delete the specified node
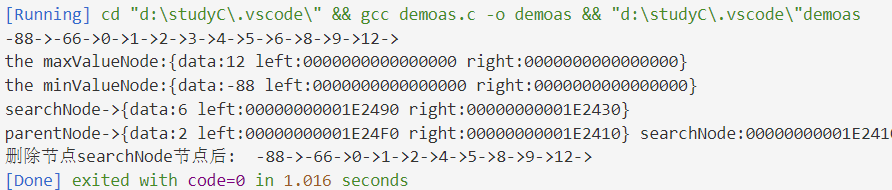
printf("Delete node searchNode After node: ");
inOrderList(pointer2);//Middle order traversal
return 0;
}The operation results are as follows: