preface
Originally, I just introduced the creation and use of red black tree from the aspects of application and simple ideological understanding. During this period of time, I want to deeply study the red black tree. I mainly refer to the content of Wikipedia and try to really realize this data structure with my own understanding and learning. Today, Koizumi will take you to roll the red and black trees! No more nonsense. Our red and black tree trip is about to start.
definition
The old rule is to tell you the definition of red black tree. Let's take a look at the introduction of red black tree on Wikipedia.
Wikipedia
Red black tree (English: red – black tree) is a self balancing binary search tree. It is a data structure used in computer science. Its typical purpose is to realize associative array. It was invented by Rudolph bell in 1972 and is called "symmetric binary B-tree". Its modern name comes from a paper written by Leo J. Guibas and Robert Sedgewick in 1978. The structure of red black tree is complex, but its operation has good worst-case running time and is efficient in practice: it can complete the search, insertion and deletion in O(log n) time, where n is the number of elements in the tree.
nature:
- Nodes are only red or black
- The root node must be black
- The leaf node must be a black empty node (NULL node)
- The left and right child nodes of the red node are black nodes
- The number of black nodes from any node to its leaf node is the same
The five properties of red black tree are the top priority, which must be kept in mind in the later process.
Algorithm departure
Next, Koizumi will take you to start our red and black tree trip. Sit down, sit down and start.
The first stop is our node. First, let's introduce the basic details of our red black tree operation.
Red black tree node
Node attribute
According to the nature of red black tree, we know that the nodes of red black tree must have at least attributes: stored value, left and right child nodes, node color and parent node.
From this point of view, it seems that it is only one more color than a general binary tree. In addition, we know that the most annoying thing of a binary tree is to record the nodes before the nodes (such as the parent node and uncle node of a node). Therefore, in order to achieve efficiency, the nodes of the red black tree also contain 5 \ Parent node.
- Stored value
- Left child node
- Right child node
- Node color
- Parent node
Find related nodes
- Find grandfather node
- Find uncle node
- Find sibling node
In fact, this wave of operation is easy to understand. It is mainly to prepare for various "rotation" operations, that is, three generations of "people" (nodes) will be involved in the rotation process. Therefore, these three operations to find relevant nodes are necessary.
For the sake of concise description, the nodes are named as follows:
Current node N, parent node P, grandfather node GP, uncle node U, brother node S, empty node NIL (note that it is not empty).
Code - node
class Node{
public Node parent = null;
public Node left = null, right = null;
public int val = 0;
public COLOR color = COLOR.RED;
public Node(){
}
public Node(Node parent, Node left, Node right, int val) {
this.parent = parent;
this.left = left;
this.right = right;
this.val = val;
}
Node grandParent() {
if (parent == null){
return null;
} else {
return parent.parent;
}
}
Node uncle() {
if (parent == grandParent().left) {
return grandParent().right;
} else {
return grandParent().left;
}
}
Node sibling() {
if (this == parent.left) {
return parent.right;
} else {
return parent.left;
}
}
}
First left-handed
Left rotation: node N floats, node P sinks, the left subtree of node N becomes the right subtree of node P, and node P becomes the left subtree of node N. Then N becomes the left child node (or right child node) of the GP node.
Here, only the case where the initial state P is the left sub node of GP is given, and the right sub tree is the same, so I won't repeat it.
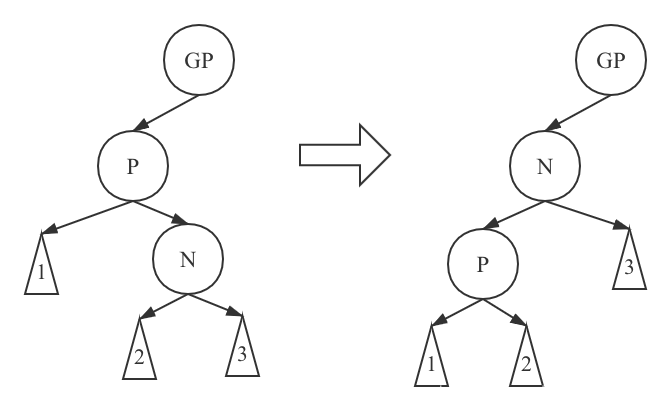
First right-handed
Right rotation: node N floats, node P sinks, the right subtree of node N becomes the left subtree of node P, and node P becomes the right subtree of node N. Then N becomes the left child node (or right child node) of the GP node.
Here, we also give the case where the initial state P is the left sub node of GP, and the right sub tree will not be repeated.
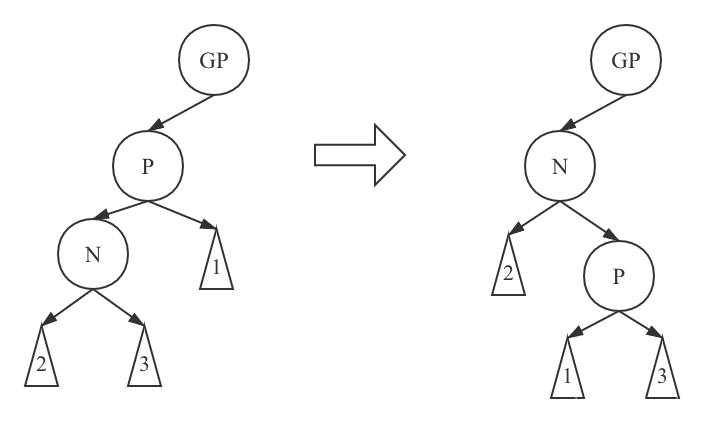
The above left-right rotation takes the deepest node as the reference n, and then there is another rotation with the above middle P node as the N node. The advantage of this is that there is no need to introduce a grandfather node (because you need to call the function to find it every time).
Second left-handed
Left rotation: the NR (right child node of n) node floats, the N node sinks, the right subtree of NR node becomes the left subtree of N node, and the N node becomes the right child node of NR node. Then NR becomes the left child node (or right child node) of P node.
Here, we also give the case where the initial state N is the left sub node of P, and the right sub tree will not be repeated.
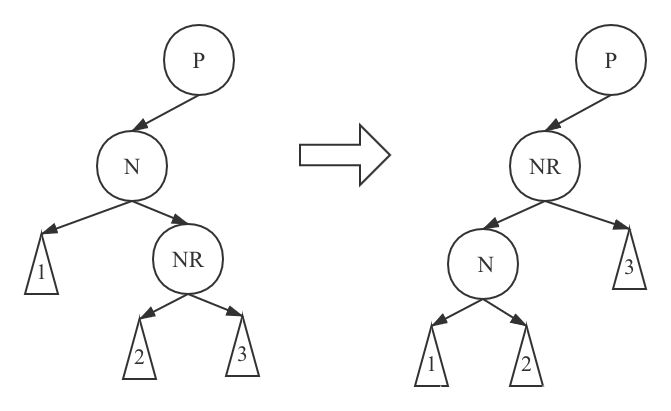
Second right-handed
Right rotation: NL node rises, N node sinks, the right subtree of NL node becomes the left subtree of N node, and N node becomes the right subtree of NL node. Then NL becomes the left child node (or right child node) of P node.
Here is also the case where the initial state N is the left child node of P.
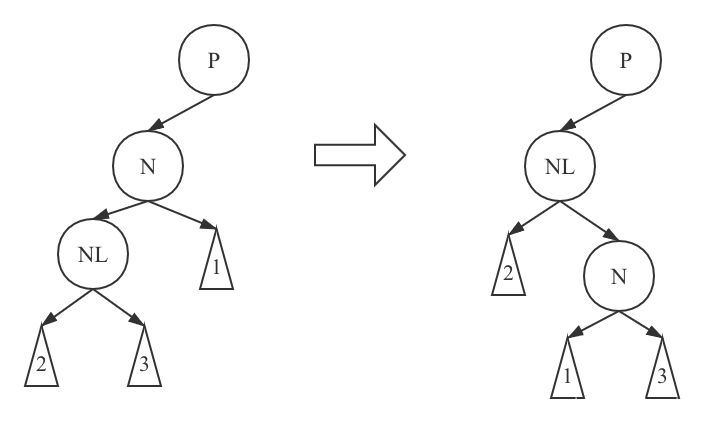
With regard to left-hand and right-hand rotation, Koizumi's principle takes the deepest node as the reference node N, that is, the first left-right rotation.
Code - rotation
public void rotate_right(Node n) {
Node gp = n.grandParent();
Node p = n.parent;
p.left = n.right;
if (n.right != NIL) {
n.right.parent = p;
}
n.right = p;
p.parent = n;
if (root == p) {
root = n;
}
n.parent = gp;
if (gp != null) {
if (gp.left == n.parent) {
gp.left = n;
} else {
gp.right = n;
}
}
}
public void rotate_left(Node n) {
Node gp = n.grandParent();
Node p = n.parent;
p.right = n.left;
if (n.left != NIL) {
n.left.parent = p;
}
n.left = p;
p.parent = n;
if (root == p) {
root = n;
}
n.parent = gp;
if (gp != null) {
if (gp.left == n.parent) {
gp.left = n;
} else {
gp.right = n;
}
}
}
Creation of red black tree
After introducing the basic operation of red black tree, we will continue to start to the creation of red black tree.
For a data structure, we mainly measure its efficiency from three aspects: query, insert and delete. Similarly, these three aspects are also the three inevitable operations of creating data structures.
query
In fact, the query process is relatively simple, which is to query according to the rules of binary search tree with time complexity O(logn). Query operations are not our main focus.
The following insertion and deletion operations need to consider whether the structure of the last tree still conforms to the five properties of red black tree, and then adjust the tree structure accordingly.
Sit still and speed up!
insert
- In order to ensure property 5 (the number of black nodes in the path from any node to leaf node is the same), the nodes inserted by default are red nodes.
- The inserted node replaces the NIL node, and the tree structure is adjusted later. (in this way, we can simplify the classification of insertion cases without considering the problem of self-contained nodes)
The two-point insertion rule is very important, and note that the subsequent situations are to adjust the tree structure after insertion, otherwise you will be confused about the classification of situations.
From simple to deep, there are many kinds of insertion operations. Let's start with the simplest.
Case 1 The inserted new node N is at the root node
Insert the position of the root node, assign the left and right child nodes as NIL nodes, and the parent node is empty.
Since the new nodes are all red, and according to property 1, the color of the root node must be black, a color change operation is also required to end the insertion operation.
Scenario 2 Insert a new node N whose parent node P is black
After the Black P node is inserted, because the inserted node is a red node, in this case, the insertion operation does not destroy any property and ends.
Scenario 3 For the inserted new node N, its parent node P is red and its tertiary node U is also red
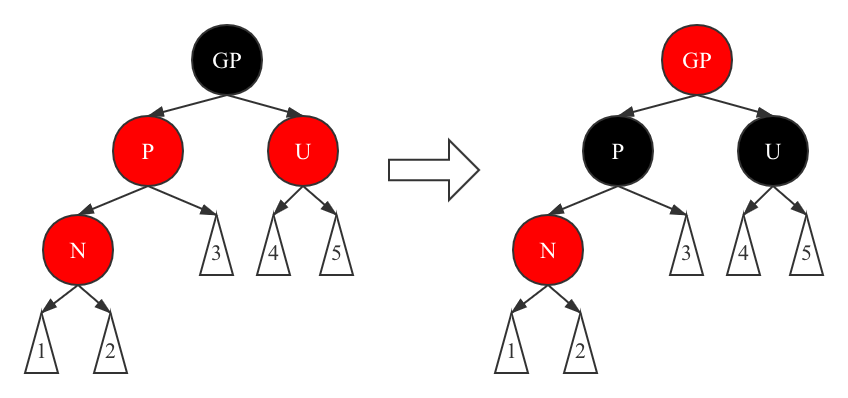
For the inserted N node, if its p node and u node are both red nodes, and the N node is also red, then it violates property 4. Because the U node is also red, then turn the GP node into red and the P and u nodes into black. This can make the tree structure conform to property 4 and the number of black nodes in the path remain the same, that is, it does not violate property 5.
However, this will lead to problems. The parent node of GP may be red or GP is the root node. At this time, you need to insert and adjust the GP node (equivalent to inserting a new red node).
Scenario 4 Insert new node n, whose parent node P is red, uncle node U is black, P is GP's left (right) child node, and N is p's right (left) child node
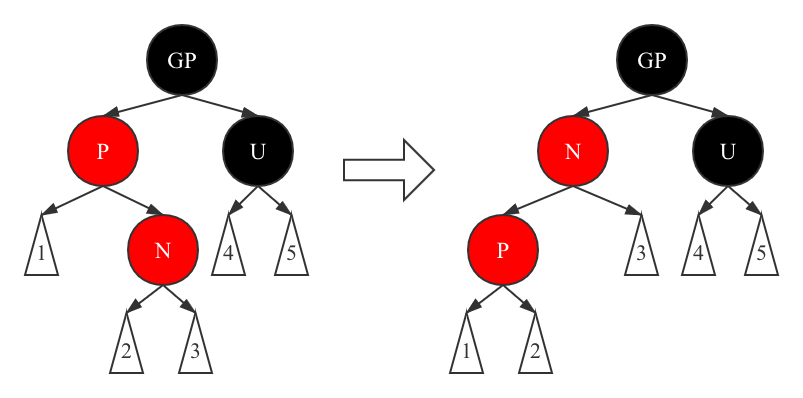
For case 4, we first make a left (right) rotation, adjust the position to the above position, and then go to case 5 to deal with it together. At this time, property 5 is still satisfied, but property 4 is not satisfied.
Scenario 5 Insert new node n, whose parent node P is red, uncle node U is black, P is GP's left (right) child node, and N is p's left (right) child node
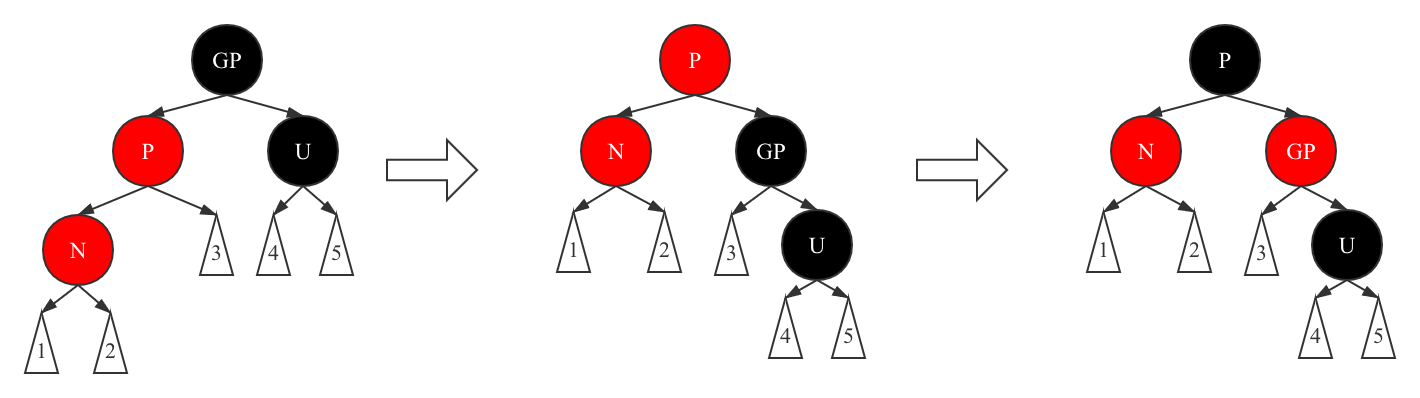
For case 5, we first rotate P right to make p float up and GP sink, which will make the number of black nodes on the left and right sides of the rotated P different (because the black GP node sinks, the left subtree of P will reach the leaf node one less black than the right subtree after rotation), so we can change the color, and P will change to black, If GP changes color to red, properties 4 and 5 can be met.
So far, the insertion operation has been explained. From the simplest insertion of the root node to the case by case discussion according to the color of the parent node and tertiary node, all cases have been covered. Now we are going to move forward at full speed. Fasten your seat belt. The relatively more complex deletion operation is about to begin.
Code - insert
private void insert(Node n, int data) {
if (n.val >= data) {
if (n.left != NIL)
insert(n.left, data);
else {
Node tmp = new Node();
tmp.val = data;
tmp.left = tmp.right = NIL;
tmp.parent = n;
n.left = tmp;
insertAdjust(tmp);
}
} else {
if (n.right != NIL)
insert(n.right, data);
else {
Node tmp = new Node();
tmp.val = data;
tmp.left = tmp.right = NIL;
tmp.parent = n;
n.right = tmp;
insertAdjust(tmp);
}
}
}
private void insertAdjust(Node n) {
//Case 1: the insertion point is the root node
if (n.parent == null){
root = n;
n.color = COLOR.BLACK;
return;
}
//Case 2: if the parent node is black, inserting a red node will not have an impact
if (n.parent.color == COLOR.RED) {
//Case 3: the parent node is red, and the uncle node is red = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
if (n.uncle().color == COLOR.RED) {//
n.grandParent().color = COLOR.RED;
n.parent.color = n.uncle().color = COLOR.BLACK;
insertAdjust(n.grandParent());
} else {
//Scenario 4: the parent node is red and the tertiary node is black. The parent node is a left subtree, and this node is a right subtree = = = = = = rotate left first and enter scenario 5
if (n.parent.right == n && n.grandParent().left == n.parent) {
rotate_left(n);
insertAdjust(n.left);
} else if (n.parent.left == n && n.grandParent().right == n.parent) {
//Case 4: the parent node is red and the tertiary node is black. The parent node is a right subtree, and the node is a left subtree = = = = = = rotate right first, and proceed to case 5
rotate_right(n);
insertAdjust(n.right);
}else if (n.parent.left == n && n.grandParent().right == n.parent) {
//Scenario 5: the parent node is red and the tertiary node is black. The parent node is the left subtree, and the node is the left subtree = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
n.grandParent().color = COLOR.RED;
n.parent.color = COLOR.BLACK;
rotate_right(n.parent);
} else {
n.grandParent().color = COLOR.RED;
n.parent.color = COLOR.BLACK;
rotate_left(n.parent);
}
}
}
}
delete
For the deletion operation, the red black tree adopts a small skill. If you want to delete a node, you need to replace the maximum value in the left subtree or the minimum value in the right subtree of the node with the node, and then delete the node used for replacement, That is, the node is equivalent to being transferred to a node with only one child (if the child node is an empty node NIL, it can also be considered as having only one child node).
In this paper, Koizumi adopts the minimum value of right subtree.
ok, then we'll know. In the end, it can be transformed into processing nodes with only one child node. Therefore, most of the following discussions are about how to adjust the structure of the tree according to the minimum position of the original right subtree after deletion.
As shown in the figure, the stored value of X is the value we want to delete (the replacement value work has been done in the early stage), and node N is the child node of this x node. Therefore, when we delete x, N will replace the position of X. the subsequent explanations are also based on such preconditions.
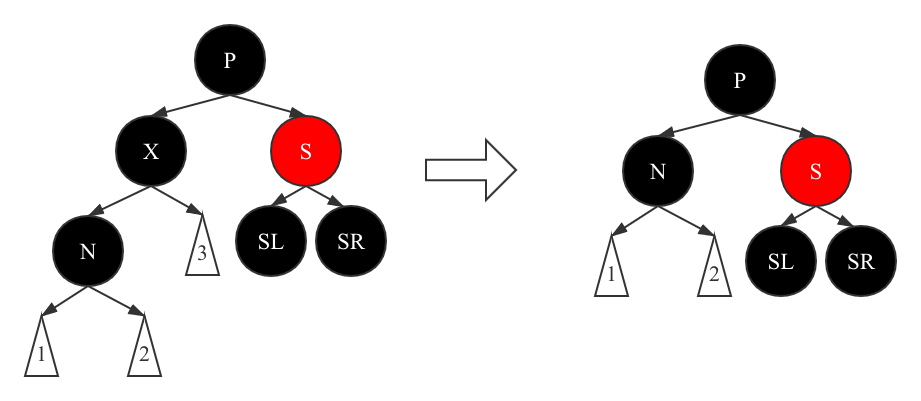
Then, when the deleted node is black, it is still discussed in several cases from simple to complex.
Case 1 Delete node X is the root node
Deleting the root is very simple. No additional operations are required. The above replacement work has been completed.
Scenario 2 Deleted node X is black and its child node N is red
Here, the five point property can be satisfied by directly changing the color of the child node to black.
Scenario 3 After deleting node x, the child node n of X, the S node of n is red, and N is the left (right) child node of parent node P
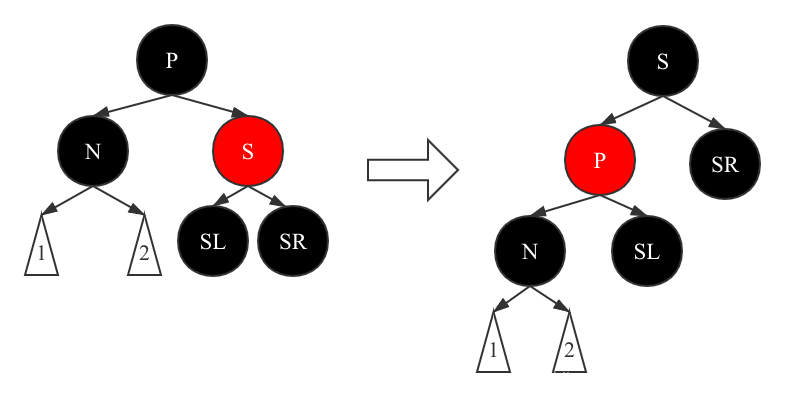
First perform a left-hand operation to make S become a new GP node of N, then the color of P node turns red and the color of S node turns black, so that the number of black nodes from S to each leaf node is the same.
However, there are still problems. There are inconsistencies in the number of paths from P to leaf nodes, that is, P-X-N is now P-N, that is, there is one less black node. At this stage, the situation continues to be pushed down and can be solved in the following situation.
Scenario 4 After deleting node x, the P node, S node, SL node and SR node of X child node n are black, and N is the left (right) child node of parent node P
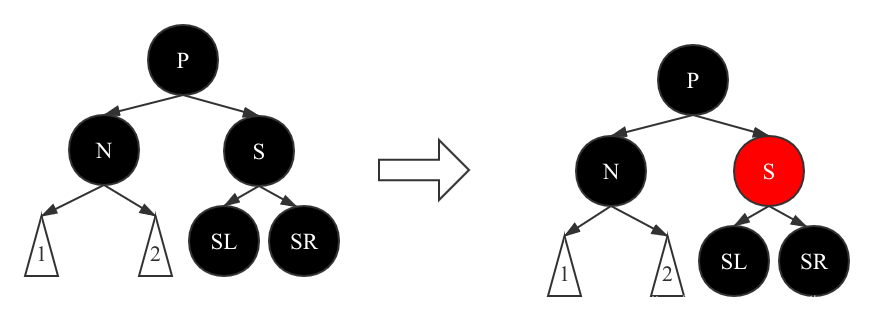
In this case, since there is less than one black node in the other paths of the P-N path, changing the S node to red can make the black nodes between the arriving paths passing through P the same.
However, the difference between the black nodes passing through P and not passing through P is still 1, so the structure of P node should be adjusted.
Scenario 5 After deleting node X, node P is red, nodes S, SL and SR are black, and N is the left (right) child node of parent node P
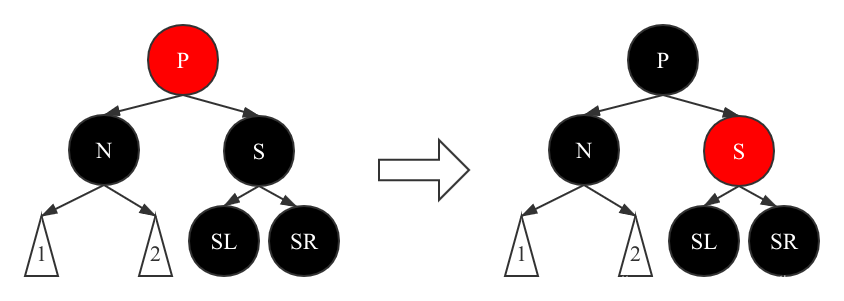
In this case, we directly choose to change color. The P node turns black to fill the missing X Black node on the N path, and the S node turns red to complement the P node.
Scenario 6 After deleting node X, S node is black, SL node is red, SR node is black, and N is the left (right) child node of parent node P
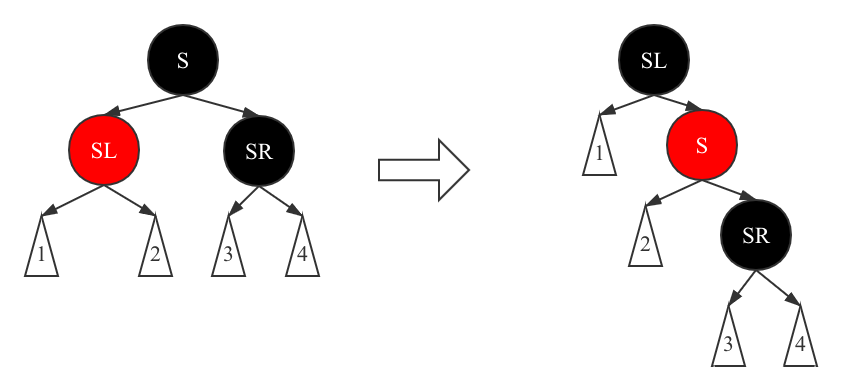
In this case, we rotate right, and then change the colors of SL and S to make this case proceed to case 6.
Scenario 7 After deleting node X, S node and SL node are black, SR node is red, and N is the left (right) child node of parent node P
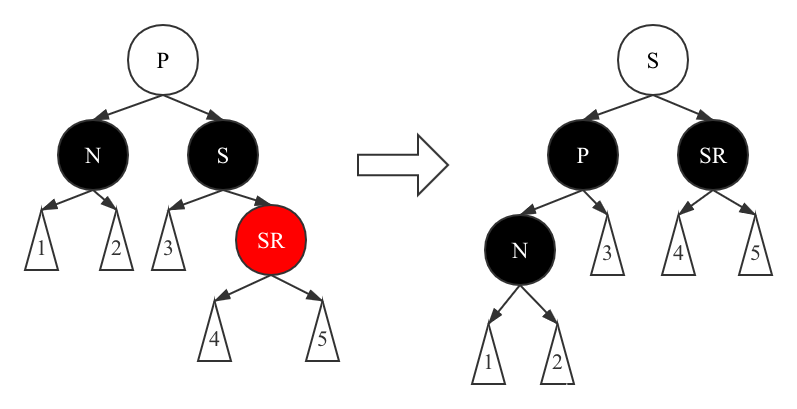
In case 7, turn S directly to the left, change the color of SR, then sink the color of P node, and keep the color of S node consistent with that of the original P node. In this way, the black nodes passing through the original P node path are fully filled, the number of black nodes in the right subtree does not change, and the property 5 is maintained.
So far, the construction of our red and black has come to an end. The article lists all the insertion and deletion operations as far as possible and restores the process. Some are easier to understand according to the basic operations of the red and black tree and pictures, so there is no too much explanation. For the insertion and deletion operations, we should consider the fourth and fifth properties, and then change color + rotate. Most of them can be solved.
Code - delete
private Node getSmallestChild(Node n) {
if (n.left== NIL) {
return n;
}
return getSmallestChild(n.left);
}
private boolean delete(Node n, int data) {
if (n.val > data) {
if(n.left == NIL) {
return false;
}
return delete(n.left, data);
} else if (n.val < data) {
if (n.right == NIL) {
return false;
}
return delete(n.right, data);
} else if (n.val == data){
if (n.right == NIL) {
deleteOneChild(n);
return true;
}
Node smallest = getSmallestChild(n.right);
int tmp = n.val;
n.val = smallest.val;
smallest.val = tmp;
deleteOneChild(smallest);
return true;
} else {
return false;
}
}
private void deleteOneChild(Node n) {
Node child = n.left == NIL ? n.right:n.left;//n node has only one subtree
if (n.parent == null && n.left == NIL && n.right == NIL) {
//Scenario 1: delete the root node without left and right child nodes;
n = null;
root = n;
return;
}
if (n.parent == null) {
//Scenario 1: delete the root node and have left or right child nodes (but only one child node).
child.parent = null;
root = child;
root.color = COLOR.BLACK;
return;
}
//Delete node X
if(n.parent.left == n) {
n.parent.left = child;
} else {
n.parent.right = child;
}
child.parent = n.parent;
if(n.color == COLOR.BLACK) {
// The deleted node X is red. In fact, no other operations are required. If it is black, it means that there will be one less black node in the path from this node to the leaf node
if (child.color == COLOR.RED) {
//Case 2: if the deleted node X is a black node and its child node is a red node, then the child node can become black.
child.color = COLOR.BLACK;
} else {
//Adjust tree structure
deleteAdjust(child);
}
}
}
private void deleteAdjust(Node n){
if (n.parent == null) {
n.color = COLOR.BLACK;
return;
}
//Scenario 3: after deleting node X, if its child node N is a black node, look at the color of its brother node S
//If it is red, you can rotate first and then change color. S turns black, P turns red, and N is still the child node of P.
// However, after that, starting from P, the path from N to leaf node will still differ by one node (the node we deleted) P-X-N = P-N
//Enter the subsequent situation
if (n.sibling().color == COLOR.RED){
n.parent.color = COLOR.RED;
n.sibling().color = COLOR.BLACK;
if (n == n.parent.left) {
rotate_left(n.sibling());
} else {
rotate_right(n.sibling());
}
}
//Case 4: after deleting node X, its child node n is a black node, and the color of the parent node, brother node S and child nodes of S are black. After changing color, adjust the parent node of n
if (n.parent.color == COLOR.BLACK && n.sibling().color == COLOR.BLACK
&& n.sibling().left.color == COLOR.BLACK && n.sibling().right.color == COLOR.BLACK) {
n.sibling().color = COLOR.RED;
deleteAdjust(n.parent);
} else if (n.parent.color == COLOR.RED && n.sibling().color == COLOR.BLACK
&& n.sibling().left.color == COLOR.BLACK && n.sibling().right.color == COLOR.BLACK){
//Case 5: after deleting node X, its child node N is a black node, the parent node is red, and the color of brother node S and its child nodes are black. Then change the color of P and S to supplement the black node in the P-N path.
n.sibling().color = COLOR.RED;
n.parent.color = COLOR.BLACK;
} else {
if (n.sibling().color == COLOR.BLACK) {
//Case 6: if N is the left child node of P, the left child node of S is red, and the right child node is black, then change color + left rotation, and then enter case 7
if (n == n.parent.left && n.sibling().left.color == COLOR.RED && n.sibling().right.color == COLOR.BLACK) {
n.sibling().color = COLOR.RED;
n.sibling().left.color = COLOR.BLACK;
rotate_left(n.sibling().left);
} else if (n == n.parent.right && n.sibling().right.color == COLOR.RED && n.sibling().left.color == COLOR.BLACK) {
n.sibling().color = COLOR.RED;
n.sibling().right.color = COLOR.BLACK;
rotate_left(n.sibling().right);
}
}
//Case 7: if N is the left child node of P, the left child node of S is black, and the right child node is red, then right rotation + color change
n.sibling().color = n.parent.color;
n.parent.color = COLOR.BLACK;
if (n == n.parent.left) {
n.sibling().right.color = COLOR.BLACK;
rotate_left(n.sibling());
} else {
n.sibling().left.color = COLOR.BLACK;
rotate_right(n.sibling());
}
}
}
Write at the end
After reading, you can leave a message below to discuss what you don't understand
Thank you for watching.
If you think the article is helpful to you, remember to pay attention to me and give me some praise and support!
Author: trickling clear spring
summary
The above knowledge points include the current mainstream application technology of Internet enterprises and the advanced architecture knowledge that can make you a "pastry". Almost every note contains actual combat content.
Many people worry that learning is easy to forget. Here is a way to teach you, that is, repeat learning.
For example, if you are learning spring annotation and suddenly find an annotation @ Aspect. You don't know what to do. You may check the source code or study through a blog. It takes half an hour to finally understand it. The next time you see @ Aspect, you are a little depressed. It seems that you studied where last time. You quickly opened the web page and learned it in five minutes.
Data collection method: stamp here for free
From the comparison between half an hour and five minutes, we can find that learning more once is one step closer to mastering knowledge.

Human nature is easy to forget. Only by constantly deepening the impression and repeated learning can we really master it. Therefore, I recommend you to read many books several times. How can there be so many geniuses? He just read books several times more than you.
Write at the end
After reading, you can leave a message below to discuss what you don't understand
Thank you for watching.
If you think the article is helpful to you, remember to pay attention to me and give me some praise and support!
Author: trickling clear spring
summary
The above knowledge points include the current mainstream application technology of Internet enterprises and the advanced architecture knowledge that can make you a "pastry". Almost every note contains actual combat content.
Many people worry that learning is easy to forget. Here is a way to teach you, that is, repeat learning.
For example, if you are learning spring annotation and suddenly find an annotation @ Aspect. You don't know what to do. You may check the source code or study through a blog. It takes half an hour to finally understand it. The next time you see @ Aspect, you are a little depressed. It seems that you studied where last time. You quickly opened the web page and learned it in five minutes.
Data collection method: stamp here for free
From the comparison between half an hour and five minutes, we can find that learning more once is one step closer to mastering knowledge.
[external chain picture transferring... (img-m1rqhjgr-16237735183)]
Human nature is easy to forget. Only by constantly deepening the impression and repeated learning can we really master it. Therefore, I recommend you to read many books several times. How can there be so many geniuses? He just read books several times more than you.