The so-called sorting is the operation of arranging a string of records in ascending or descending order according to the size of one or some keywords. Sorting algorithm is how to arrange records according to requirements. There are roughly eight commonly used sorting algorithms: insertion sort (direct insertion sort, Hill sort), selection sort (simple selection sort, heap sort), exchange sort (bubble sort, quick sort), merge sort and cardinal sort.
1, Direct insert sort
Algorithm idea: divide the array to be sorted into two parts. One part is the sorted elements and the other part is the elements to be inserted. If the selected elements are smaller than the sorted elements, exchange them until all elements are compared.
Sorting process:
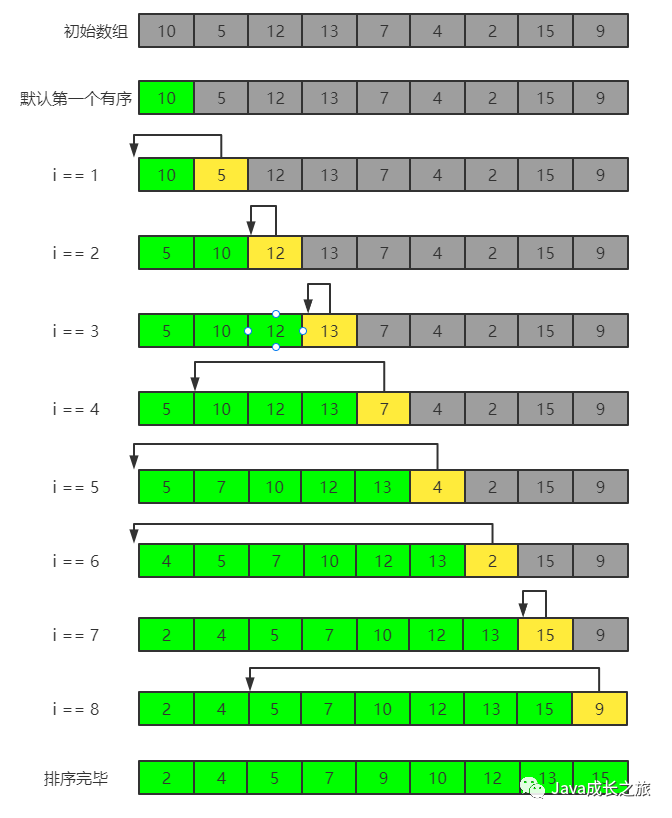
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
insertSort(arr);
}
public static void insertSort(int[] arr) {
//The first element is ordered by default
for (int i = 1; i < arr.length; i++) {
//Start with the second element
int temp = arr[i];
for (int j = i; j >= 0; j--) {
//If the current element is not the first and the current element is greater than temp, move backward
if (j > 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
} else {
arr[j] = temp;
break;
}
}
System.out.println(Arrays.toString(arr));
}
}Execution result:
[5, 10, 12, 13, 7, 4, 2, 15, 9] [5, 10, 12, 13, 7, 4, 2, 15, 9] [5, 10, 12, 13, 7, 4, 2, 15, 9] [5, 7, 10, 12, 13, 4, 2, 15, 9] [4, 5, 7, 10, 12, 13, 2, 15, 9] [2, 4, 5, 7, 10, 12, 13, 15, 9] [2, 4, 5, 7, 10, 12, 13, 15, 9] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: best case O(n), worst case O(n) ²), Average complexity O(n) ²)
Space complexity: only temp has one space, O(1)
2, Hill sort
Algorithm idea: first divide the whole sequence to be sorted into several subsequences for direct insertion sorting. When the records in the whole sequence are "basically orderly", then directly insert and sort all elements.
Sorting process:
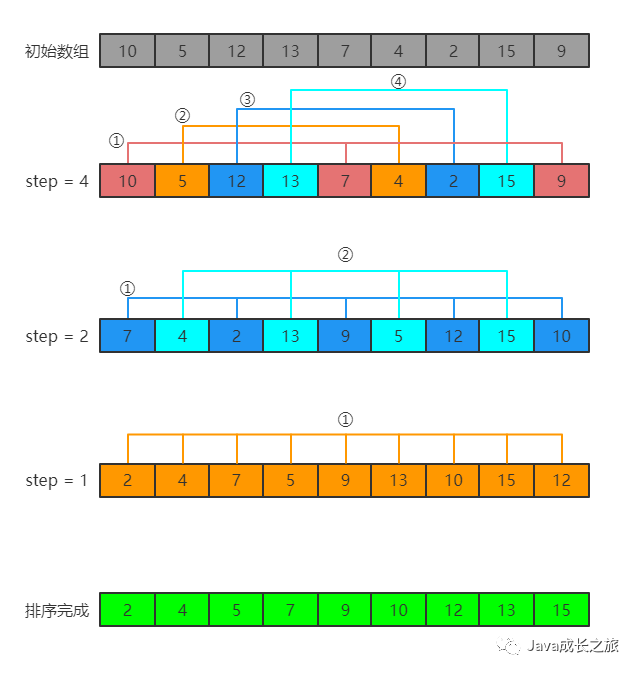
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
shellSort(arr);
}
public static void shellSort(int[] arr) {
//Find step
int step = arr.length / 2;
//When the step size is greater than 0 and equal to 1, it is equivalent to a direct insertion sort
while (step > 0) {
//Each sequence starts from the second, and now it is a direct insertion sort for each sequence
for (int i = step; i < arr.length; i++) {
//If the i-th element is larger than the i-step element, insert it directly. If it is less than, insert this if after moving the ordered table, which can be omitted
if (arr[i] < arr[i - step]) {
//Location of the previous element
int j = i - step;
//Temporarily stores the current element
int temp = arr[i];
//Element backward
arr[i] = arr[i - step];
//Find the location where the element is stored j + step
while (j >= 0 && arr[j] > temp) {
arr[j + step] = arr[j];
j = j - step;
}
arr[j + step] = temp;
}
}
step = step / 2;
System.out.println(Arrays.toString(arr));
}
}Execution result:
[7, 4, 2, 13, 9, 5, 12, 15, 10] [2, 4, 7, 5, 9, 13, 10, 15, 12] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity:
Best case O(nlogn), worst case O(n) ²), Average complexity O(n^1.5)
Space complexity: only temp has one space, O(1)
3, Simple selection sort
Algorithm idea: in a group of numbers to be sorted, select the smallest (or largest) number to exchange with the number at the first position; Then, among the remaining numbers, find the smallest (or largest) number to exchange with the number at the second position, and so on until the Nth-1 element (the penultimate number) is compared with the nth element (the last number).
Sorting process:
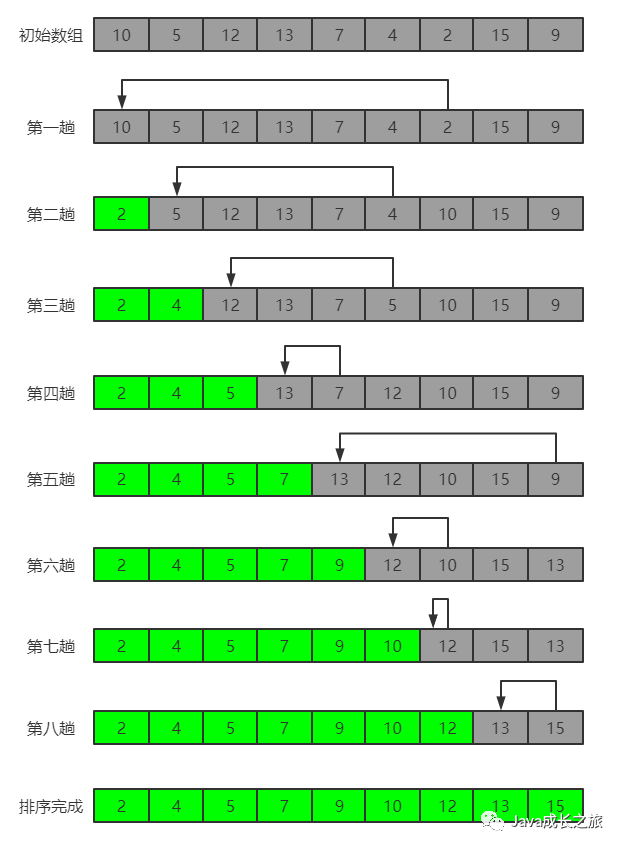
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
selectSort(arr);
}
public static void selectSort(int[] arr) {
//Each time, select the minimum value from the remaining elements and put it in the first position
for (int i = 0; i < arr.length - 1; i++) {
//Record the minimum coordinates of each trip
int min = i;
//Find the minimum value of each trip, find the coordinates first, and then exchange to reduce the number of exchanges
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//Element exchange
if (min != i) {
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
}Execution result:
[2, 5, 12, 13, 7, 4, 10, 15, 9] [2, 4, 12, 13, 7, 5, 10, 15, 9] [2, 4, 5, 13, 7, 12, 10, 15, 9] [2, 4, 5, 7, 13, 12, 10, 15, 9] [2, 4, 5, 7, 9, 12, 10, 15, 13] [2, 4, 5, 7, 9, 10, 12, 15, 13] [2, 4, 5, 7, 9, 10, 12, 15, 13] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: best case O(n) ²), Worst case O(n) ²), Average complexity O(n) ²)
Space complexity: only temp has one space, O(1)
Tips: selective sorting can be improved. Not only the maximum value can be found each time, but also the minimum value can be found and put to the end, so as to reduce the number of trips by half.
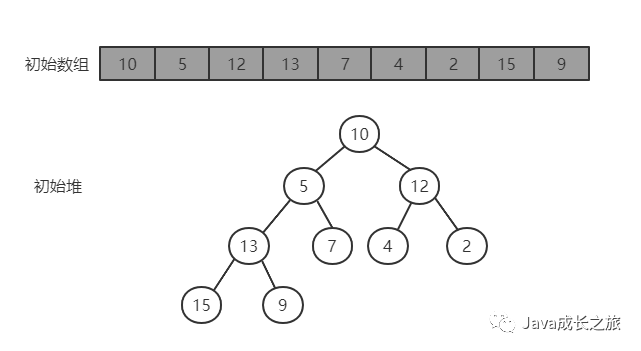
4, Heap sort
The definition of heap is as follows: the sequence {k1,k2, ···, kn} of n elements is called heap if and only if the following relationship is satisfied:
Ki < = K (2I) or ki > = K (2I)
Ki < = K (2I + 1) or ki > = K (2I + 1)
According to the characteristics of the reactor, the reactor can be divided into large top reactor and small top reactor
Large top heap: the value of each node is greater than or equal to the value of its left and right child nodes
Small top heap: the value of each node is less than or equal to the value of its left and right child nodes
Algorithm idea:
① Create minimum heap: reorder all data in the heap
② Maximum heap adjustment: adjust the end terminal node of the heap so that the child node is always greater than the parent node
③ Heap sorting: remove the root node of the first data and do the recursive operation of minimum heap adjustment
Sorting process:
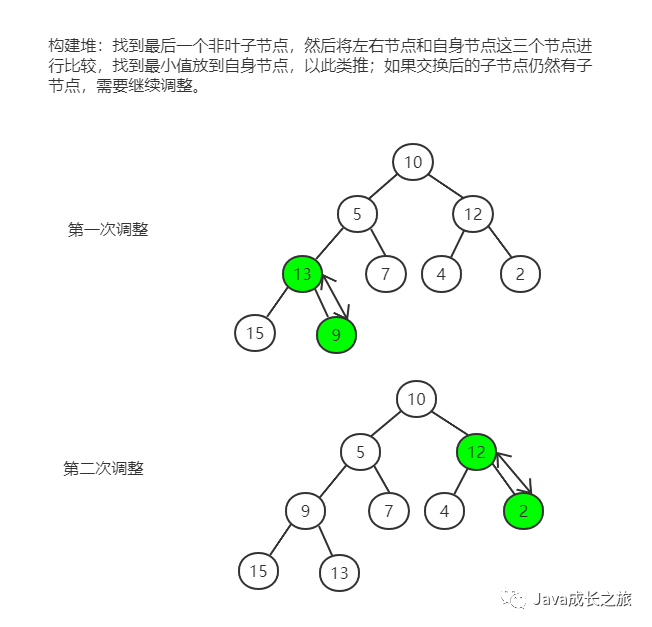
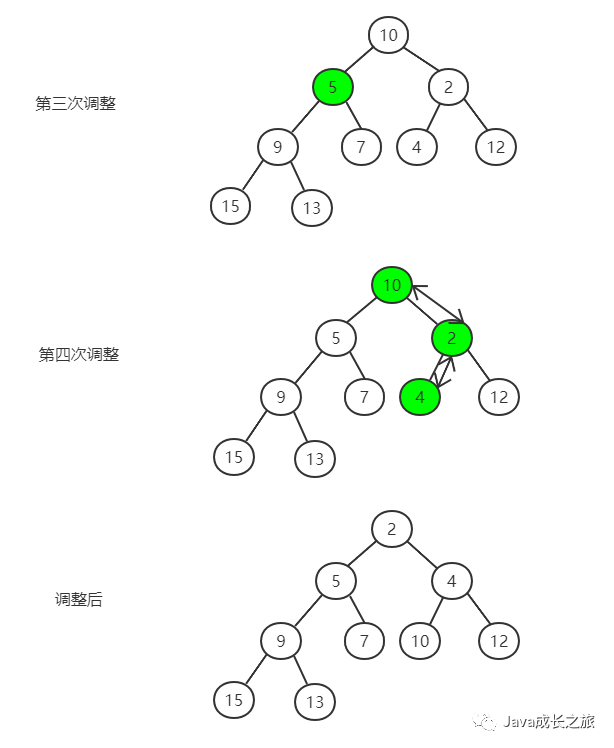
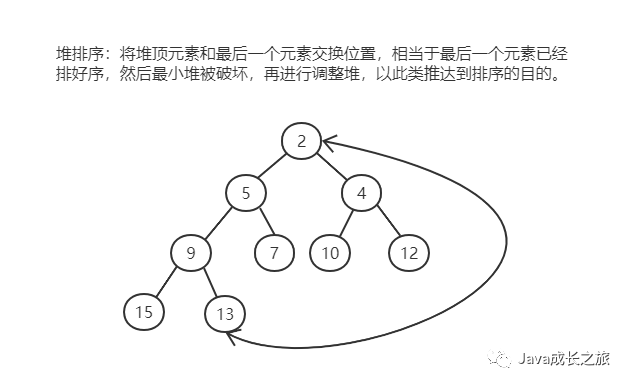
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
heapSort(arr);
}
public static void heapSort(int[] arr) {
//Initial heap
buildHeap(arr, arr.length);
//Adjust the sequence from the last element
System.out.println("Heap sort start");
for (int i = arr.length - 1; i > 0; i--) {
//Swap the top element arr[0] and the last element in the heap
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//Adjust the top of the heap every time you swap the top of the heap element with the last element in the heap
adjustHeap(arr, 0, i);
}
System.out.println("End of heap sort");
}
/**
* Build heap
*
* @param arr array
* @param len length
*/
private static void buildHeap(int[] arr, int len) {
System.out.println("Build heap start");
for (int i = (len - 1) / 2; i >= 0; i--) {
adjustHeap(arr, i, len);
}
System.out.println("End of build heap");
}Execution result:
Build heap start [10, 5, 12, 13, 7, 4, 2, 15, 9] [10, 5, 12, 9, 7, 4, 2, 15, 13] [10, 5, 2, 9, 7, 4, 12, 15, 13] [10, 5, 2, 9, 7, 4, 12, 15, 13] [2, 5, 4, 9, 7, 10, 12, 15, 13] End of build heap Heap sort start [4, 5, 10, 9, 7, 13, 12, 15, 2] [5, 7, 10, 9, 15, 13, 12, 4, 2] [7, 9, 10, 12, 15, 13, 5, 4, 2] [9, 12, 10, 13, 15, 7, 5, 4, 2] [10, 12, 15, 13, 9, 7, 5, 4, 2] [12, 13, 15, 10, 9, 7, 5, 4, 2] [13, 15, 12, 10, 9, 7, 5, 4, 2] [15, 13, 12, 10, 9, 7, 5, 4, 2] End of heap sort
Tips: the output of the smallest heap is in reverse order, and the largest heap can be constructed by arranging in positive order
Time complexity:
Best case O(nlogn), worst case O(nlogn), average complexity O(nlogn)
Space complexity: only temp has one space, O(1)
5, Bubble sorting
Algorithmic idea: in the sequence to be sorted, compare and adjust the two adjacent numbers from top to bottom for all elements that have not been sorted yet, so that the larger number sinks and the smaller one rises, just like bubbles floating up. If their order is wrong, exchange them.
Sorting process:
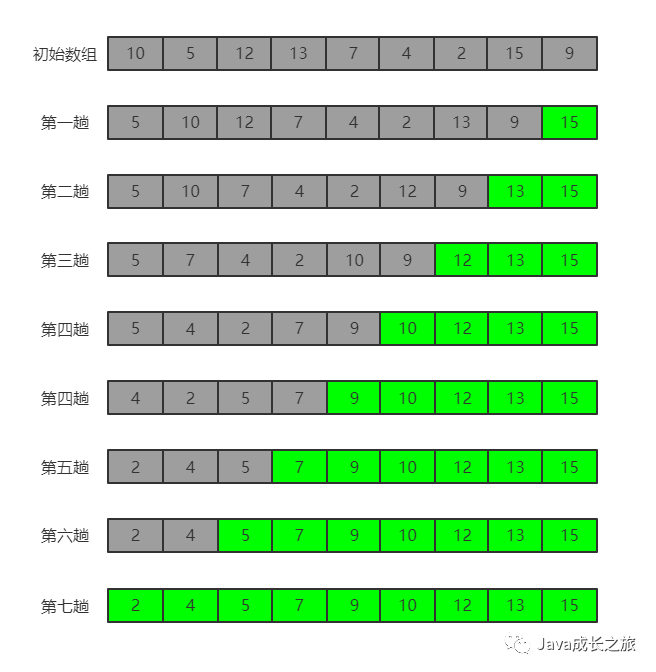
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
bubbleSort(arr);
}
public static void bubbleSort(int[] arr) {
//Outer loop control times
for (int i = arr.length - 1; i > 0; i--) {
//Node comparison can only compare to the ith element
for (int j = 0; j < i; j++) {
//Exchange element
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println(Arrays.toString(arr));
}
}Execution result:
[5, 10, 12, 7, 4, 2, 13, 9, 15] [5, 10, 7, 4, 2, 12, 9, 13, 15] [5, 7, 4, 2, 10, 9, 12, 13, 15] [5, 4, 2, 7, 9, 10, 12, 13, 15] [4, 2, 5, 7, 9, 10, 12, 13, 15] [2, 4, 5, 7, 9, 10, 12, 13, 15] [2, 4, 5, 7, 9, 10, 12, 13, 15] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: best case O(n), worst case O(n) ²), Average complexity O(n) ²)
Space complexity: only temp has one space, O(1)
Tips: we can see that the last few times are unnecessary, so we can stop sorting when there is no element exchange, so as to reduce the cycle comparison time.
6, Quick sort
Algorithm idea: select a benchmark and divide the elements to be arranged into two parts through one-time sorting. One part is larger than the benchmark value and the other part is smaller than the benchmark value. Then the records of these two parts can be sorted separately to achieve the order of the whole sequence. (the idea of divide and rule)
Sorting process:
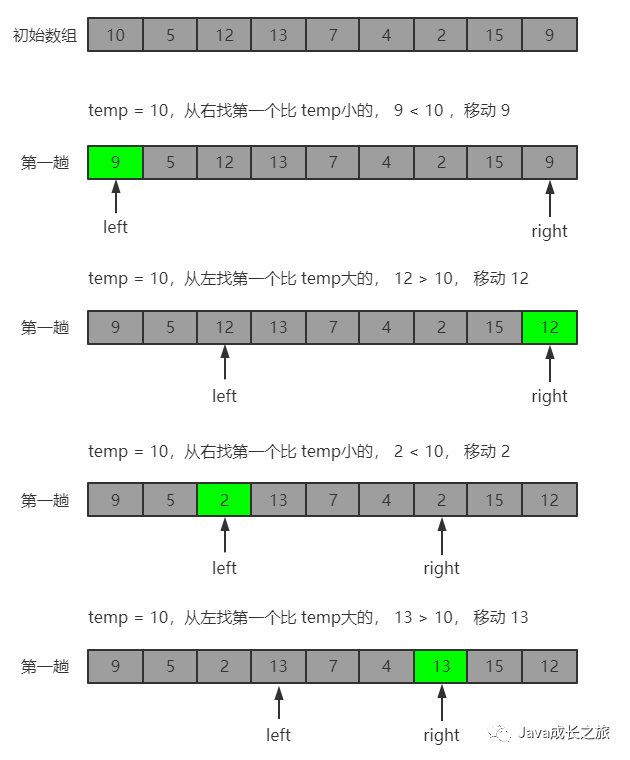
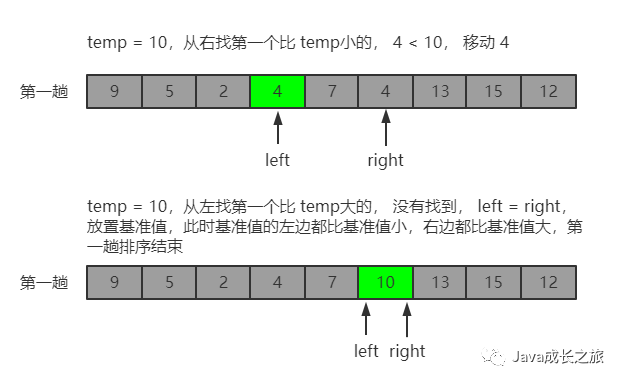
At this time, benchmark 10 finds its position. Then, by analogy, the recursive sorting of left sequence and right sequence can make the whole sequence orderly.
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int low, int high) {
//Stop condition of recursion
if (arr.length <= 0) {
return;
}
//Stop condition of recursion
if (low >= high) {
return;
}
int left = low;
int right = high;
//The datum is based on the first element of the sequence
int temp = arr[left];
while (left < right) {
//Find one smaller than the datum from the right
while (left < right && arr[right] >= temp) {
right--;
}
arr[left] = arr[right];
//Find one larger than the datum from the left
while (left < right && arr[left] <= temp) {
left++;
}
arr[right] = arr[left];
}
//Put in reference value
arr[left] = temp;
System.out.println(Arrays.toString(arr));
//Recursive sorting left sequence
quickSort(arr, low, left - 1);
//Recursive sort right sequence
quickSort(arr, left + 1, high);
}Execution result:
[9, 5, 2, 4, 7, 10, 13, 15, 12] [7, 5, 2, 4, 9, 10, 13, 15, 12] [4, 5, 2, 7, 9, 10, 13, 15, 12] [2, 4, 5, 7, 9, 10, 13, 15, 12] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: best case O(nlogn), worst case O(n) ²), Average complexity O(nlogn)
Spatial complexity: best case O(logn), worst case O(n)
7, Merge sort
Algorithm idea: merge sorting is to combine two (or more) ordered sequences into a new ordered sequence, that is, the sequence to be sorted is divided into several subsequences, and each subsequence is ordered. Then the ordered subsequences are combined into an overall ordered sequence.
Sorting process:
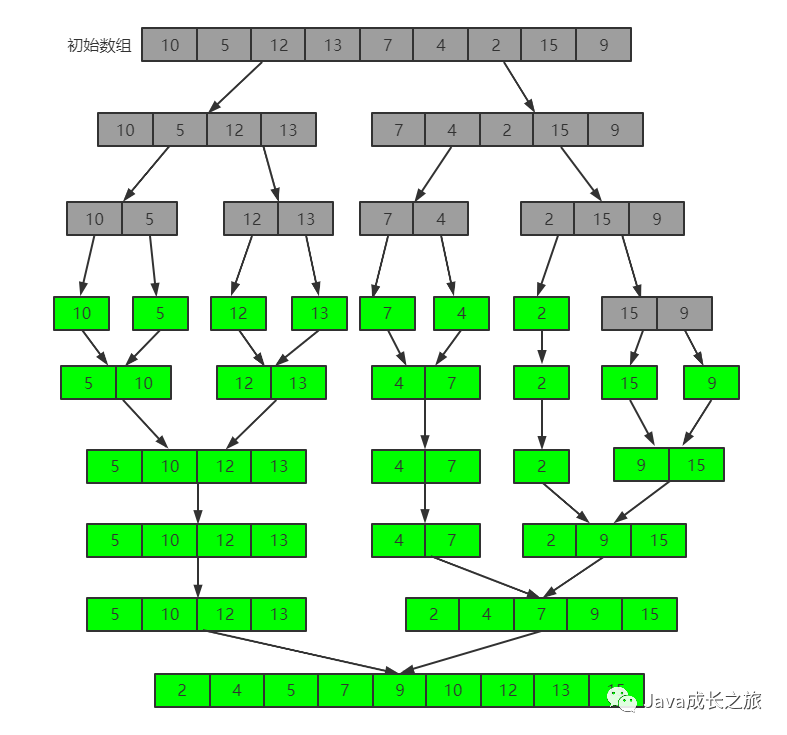
Tips: as like as two peas, we just did not move the same thing down.
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
mergeSort(arr);
}
public static int[] mergeSort(int[] arr) {
if (arr.length == 1) {
return arr;
}
int mid = arr.length / 2;
int[] left = Arrays.copyOfRange(arr, 0, mid);
int[] right = Arrays.copyOfRange(arr, mid, arr.length);
System.out.println("Consolidation:" + Arrays.toString(left) + "\t" + Arrays.toString(right));
return merge(mergeSort(left), mergeSort(right));
}
/**
* Merge two ordered arrays
*
* @param left Array 1
* @param right Array 2
* @return New array
*/
private static int[] merge(int[] left, int[] right) {
//Combined array size
int[] mergeArr = new int[left.length + right.length];
//i is the left coordinate, j is the right coordinate, and k is the new array coordinate
int i = 0, j = 0, k = 0;
//Below is the merging of two ordered arrays. At this time, the arrays left and right passed in must be ordered
while (i < left.length && j < right.length) {
mergeArr[k++] = left[i] <= right[j] ? left[i++] : right[j++];
}
//Merge the remaining elements of the left array
while (i < left.length) {
mergeArr[k++] = left[i++];
}
//Merge the remaining elements of the right array
while (j < right.length) {
mergeArr[k++] = right[j++];
}
System.out.println(Arrays.toString(mergeArr));
return mergeArr;
}Execution result:
Consolidation:[10, 5, 12, 13] [7, 4, 2, 15, 9] Consolidation:[10, 5] [12, 13] Consolidation:[10] [5] [5, 10] Consolidation:[12] [13] [12, 13] [5, 10, 12, 13] Consolidation:[7, 4] [2, 15, 9] Consolidation:[7] [4] [4, 7] Consolidation:[2] [15, 9] Consolidation:[15] [9] [9, 15] [2, 9, 15] [2, 4, 7, 9, 15] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: best case O(nlogn), worst case O(nlogn), average complexity O(nlogn)
Space complexity: O(n)
8, Cardinality sort
Algorithm idea: unify all values to be compared (positive integers) into the same digit length, and fill zero in front of the shorter digit. Then, start from the lowest order and sort once in turn. In this way, from the lowest order to the highest order, the sequence becomes an ordered sequence.
Sorting process:
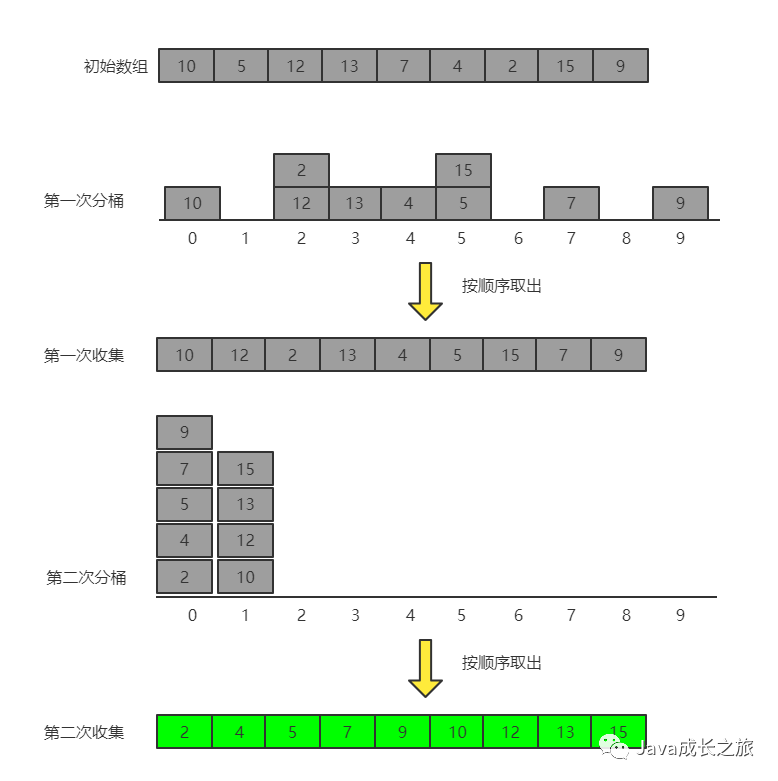
Code implementation:
public static void main(String[] args) {
int[] arr = new int[]{10, 5, 12, 13, 7, 4, 2, 15, 9};
radixSort(arr);
}
public static void radixSort(int[] arr) {
if (arr.length == 1) {
return;
}
//Find the maximum value in the array
int max = 0;
for (int item : arr) {
if (max < item) {
max = item;
}
}
//Get the maximum number of digits
int maxDigit = 1;
while (max / 10 > 0) {
maxDigit++;
max = max / 10;
}
//Apply for bucket space
int[][] buckets = new int[10][arr.length];
int divisor = 10;
for (int i = 0; i < maxDigit; i++) {
//There are only 10 numbers. key is the value of each position. Value stores the number of this value
int[] bucketLength = new int[10];
//Assign: assign all elements to the bucket
for (int value : arr) {
int whereBucket = (value % divisor) / (divisor / 10);
buckets[whereBucket][bucketLength[whereBucket]] = value;
//Number of this bit
bucketLength[whereBucket]++;
}
//Collection: take out the data in different barrels
int k = 0;
for (int j = 0; j < buckets.length; j++) {
for (int l = 0; l < bucketLength[j]; l++) {
arr[k++] = buckets[j][l];
}
}
System.out.println(Arrays.toString(arr));
divisor = divisor * 10;
}
}Execution result:
[10, 12, 2, 13, 4, 5, 15, 7, 9] [2, 4, 5, 7, 9, 10, 12, 13, 15]
Time complexity: d: number of digits, r: cardinality, n: number of sequences
Best case O(d*(n+r)), worst case O(d*(n+r)), average complexity O(d*(n+r))
Space complexity: O(n+r)
That's the end of today's sharing. Remember to praise your little friends.
Pay attention to the official account number JavaGrowUp. We won't get lost in the next stage to get more exciting content.
