Sum of K numbers
Title Description: give you an array composed of any N numbers. Given a target value target, it is required to find K numbers so that the sum of these K numbers is target. It is required to output the combination of all k digits that meet this condition, and the combination shall not be repeated
(take K=4 as an example)
Input: num = [1,0, - 1,0, - 2,2], target = 0 Output: [[- 2, - 1,1,2], [- 2,0,0,2], [- 1,0,0,1]]
As shown in the question, in the case of knowing K, we can set k-layer cycle for each possible N1 NK, making N1 + Save when NK = = target, but obviously, when k is not clear, we can't set the loop. In other words, this method is too redundant, and according to the data size requirements of the subject, this violent enumeration must timeout
Then we can complete this problem with recursion. We know that to solve the problem with scale N, we need to use the solution of scale N-1. Then, suppose that we need to add four numbers to target, and assume that a value has been determined to be I, then we only need to solve the problem with three numbers added to target-i, and the solution of the latter is homomorphic with that of the former. Therefore, We can write functions for recursion
For this problem, we can sort first to make the search process as short as possible. After sorting, we can mainly omit the following: when finding a target, use double pointers to point to the maximum and minimum values respectively (strictly speaking, it should be the starting value). When it is found that the sum is not equal to the target, we will make one party's pointer move. For the principle, please refer to "the first N large numbers", This will speed up the search
Starting from the simple method, the above method can be realized directly, but the focus is how to store the "results"?, We should use a vector array to store the answers. Before entering a layer, we first put them in, and then carry out the so-called recursion. No matter whether the recursion result is finally found or not, we should pop back the things put in this layer (if we don't find them, we have to retreat and continue to find them). When we keep pushing back, we reach a critical condition, It is found that the target is 0 at this time, indicating that the last number has been found. We put this vector array into a vecotr < vector < int > > array, which is specially used to store answers
The implementation code of the simple version is as follows
void ksum(int k, int start, int target, int num[])//K is the number of digits and start is the starting position
{
if (k == 0)
{
if (target == 0)
{
ans.push_back(tmp);
}
return;
}
else
{
for (int i = start;i <=len-k;i++) //If we need to find four digits, after we fix one, at least
//There are three digits in the remaining array that we can find
//Otherwise, after fixing one, the rest are less than three, how can we put together four?
//The number of K is the same.
{
if (i > start && num[i] == num[i - 1])continue;
tmp.push_back(num[i]);
ksum(k - 1, i + 1, target - num[i], num);
tmp.pop_back();
}
}
}Note if (I > Start & & num [i] = = num [I - 1]) continue here; Why do we do this? The answer is de duplication. It is found that the principle of de duplication is not particularly in-depth on the Internet. Here is a detailed explanation: Take - 2-1-101 as an example. When we fix the first - 1, we need to find target - (- 1) in - 101, but when we fix the second - 1, we need to find target - (- 1) in 0 1 and observe carefully, We found that if 0 1 is a subset of - 1 0 1, the subset has already been found in the process of finding the complete set! This is why the judgment condition will be repeated if it is not added! Suppose that the target value we need is 1, and the answer of - 1 0 1 is 0 1, and the answer of 0 1 is also 0 1, but the two search processes are fixed with - 1 in two different positions, but each time we search, we will throw in an element, which is the source of repetition. To be clear, we can find it in the subset and the whole set, but we must visit it shorter and shorter, When the complete set has been found, the subset does not have to be found. The key point is that the search values are the same.
The running results are as follows: (take the case of K==4,target=0,num.length=6 as an example)
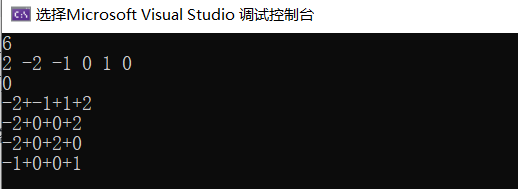
Of course, this simple version only solves the problem of fewer numbers. It will definitely time out on LeetCode. We found that when we find the last number, we can make a direct judgment without recursion. Therefore, we directly write the case of n==2
The advanced version code is as follows:
void kksum(int k, int start, int target, int num[])
{
if (k > 2)
{
for (int i = start;i <= len - k;i++)
{
if (i > start && num[i] == num[i - 1])continue;
else
{
tmp.push_back(num[i]);
kksum(k - 1, i + 1, target - num[i], num);
tmp.pop_back();
}
}
}
else if(k==2)
{
int left = start,right=len-1;
while (left < right)
{
if (num[left] + num[right] == target)
{
tmp.push_back(num[left]);
tmp.push_back(num[right]);
ans.push_back(tmp);
tmp.pop_back();
tmp.pop_back();
while (left < right && num[left] == num[left + 1])left++;
while (left < right && num[right] == num[right - 1])right--;
left++;
right++;
}
else if (num[left] + num[right] > target)
{
do
{
right--;
} while (left<right&&num[right]==num[right+1]);
}
else if (num[left] + num[right] < target)
{
do
{
left++;
} while (left < right && num[left] == num[left-1]);
}
}
return;
}
}It is worth noting that when our result is different from the target, the pointer does not have to move and ends immediately. We judge whether the value pointed by the pointer after moving is the same. If it is the same, even the next while judgment, the result is the same. Therefore, we need two do while loops to make the left and right pointers move continuously, Until the pointed value is not equal to the previously pointed value
Second, after we find the result, not only one side will be moved. If only one side is moved, because the array is orderly, one of the two addends must be smaller or larger than the previous one. No matter how one-way moving is not in line with the target, we can move at the same time, so as to ensure that one becomes larger and the other becomes smaller. Of course, you can move unilaterally and only do while once more, If there are n answers, conduct n more while.
The principle has been clear. The code is modified into leetcode and passed, but the efficiency is still a little low
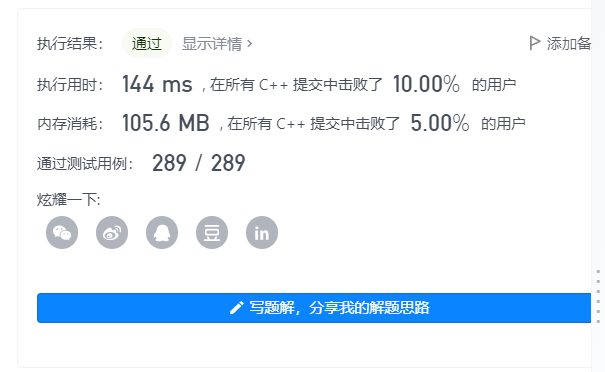
Of course, since we already know that K=4, we can directly write four layers of for or while loops
The code is shown in the figure below:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>>ans;
if (nums.size() < 4)return ans;
sort(nums.begin(), nums.end());
int len = nums.size();
for (int i = 0;i <= len - 4;i++)
{
if (i > 0 && nums[i] == nums[i - 1])continue;
tmp.push_back(nums[i]);
for (int j = i + 1;j <= len - 3;j++)
{
if (j > i+1 && nums[j] == nums[j - 1])continue;
tmp.push_back(nums[j]);
int left = j + 1, right = len - 1;
while (left < right)
{
if (nums[left] + nums[right] == (target-nums[i]-nums[j]))
{
tmp.push_back(nums[left]);
tmp.push_back(nums[right]);
ans.push_back(tmp);
tmp.pop_back();
tmp.pop_back();
while (left < right && nums[left] == nums[left + 1])left++;
while (left < right && nums[right] == nums[right - 1])right--;
left++;
right--;
}
else if (nums[left] + nums[right] > (target - nums[i] - nums[j]))
{
do
{
right--;
} while (left < right && nums[right] == nums[right + 1]);
}
else if (nums[left] + nums[right] < (target - nums[i] - nums[j]))
{
do
{
left++;
} while (left < right && nums[left] == nums[left - 1]);
}
}
tmp.pop_back();
}
tmp.pop_back();
}
return ans;
In this way, the subspace can be more open without entering the function step by step. The submitted results are as follows:
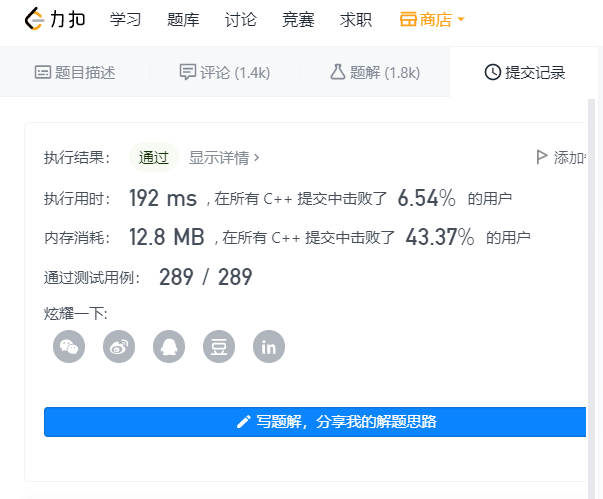
Optimization part
Because the array is ordered, some unnecessary judgment and recursion can be omitted directly. For example, in this problem, we need a fixed value, but not every number can be used as this fixed value. Assuming that this number is a fixed value, we have to choose three more numbers. If we add this number to the largest number in the first three digits, it is still less than target, Then you can continue directly to the next i, because even the largest three digits can't pull this number to the target, not to mention the numbers smaller than these numbers. On the contrary, if the target is divided into k parts on average, even the fixed value is greater than the average value, not to mention the ones larger than the fixed value, which will certainly be greater than the target. Therefore, there are the following two optimizations
1. When K numbers are taken to meet the target, if the sum of the current value and the previous K-1 is still less than the target, continue directly to start the next round
2. When the current value is less than the average K value of target, it means that the number added back must be greater than target. break this layer cycle directly.
Code part omitted
Optimized results: (recursive version)
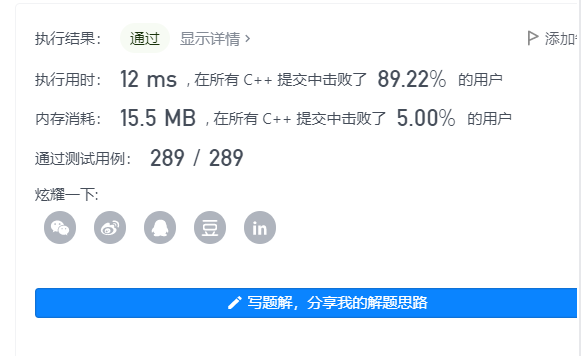
(for circular version)
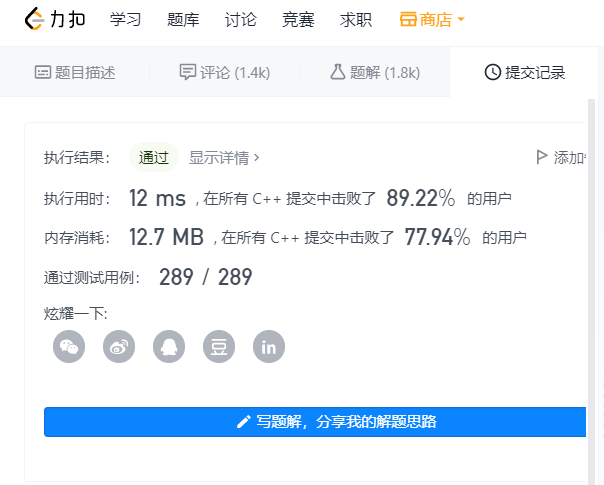
After the for loop is optimized, it is almost the best version of this solution. Of course, you can do it in more detail. return the abnormal behavior directly, which can improve the running efficiency of the program
I hope this article can help you. There are some inappropriate and wrong places in the article. Please don't hesitate to comment!