emmm,dp problem is really magical. If you want to get the equation of state, you can take off immediately. If you can't think of it and have no idea, then It is suggested to write after a good meal. It may be faster In fact, dp is more an experience. If you see more, you will write faster, because the state of this kind of questions means that you are already familiar with it. Well, without much gossip, continue the dp journey.

Digital triangle

Digital triangle is also a classical dp problem, which is as common as knapsack. If this problem is to be classified, it should belong to a kind of linear dp. The so-called linear dp means that our dp equation (equation of state) has an obvious linear relationship (linear when updated). So what can digital triangles do?

 

Given a digital triangle as shown in the figure below, starting from the top, at each node, you can choose to move to the node at the lower left or to the node at the lower right, and go all the way to the bottom. It is required to find a path to maximize the sum of numbers on the path.

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

Digital triangles can be made in two ways, from top to bottom or from bottom to top:

From top to bottom

 

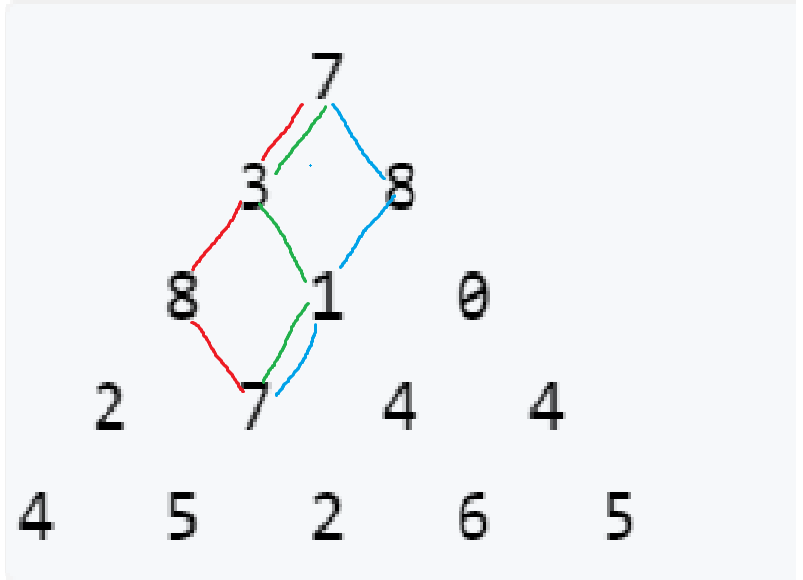
We can see that when we get to point 7, we can arrive from three paths: red, green, blue, so we can observe that the path to point 7 and either come from the top left or the top right. In this case, we can start writing our equation of state. Why can we write it directly, because dp - dynamic programming, In fact, it is a method to deal with sub problems with similar characteristics.

 

Equation of state: F [i] [J] = max (upper left + a [i] [J], upper right + a [i] [J])

State representation: the maximum value of the sum of the paths to i and j

Then this question is easy to write:

const int N = 510;
int f[N][N];
int a[N][N];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++) scanf("%d",&a[i][j]);
    
    for(int i=0;i<=n;i++)
        for(int j=0;j<=i+1;j++)//Considering the boundary problem, when initializing, pay attention to one more place to prevent the boundary problem when the rightmost number takes the number from the upper right corner
            f[i][j]=-10000;
   
    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++)
            f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
    
    int res=-10000;
    for(int i=1;i<=n;i++)res=max(res,f[n][i]);
    printf("%d",res);
    return 0;
}

From bottom to top

Compared with falling from the top, it is actually simpler and easy to think, because there is no need to consider the boundary problem.

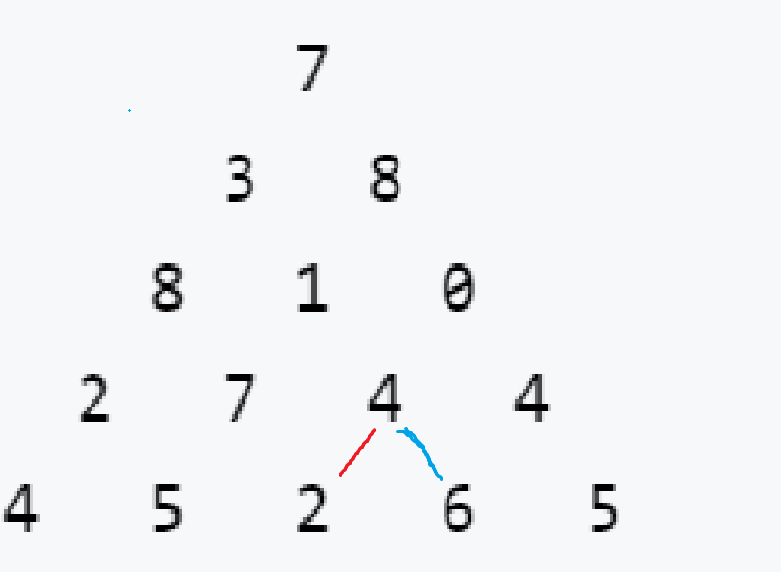
Because the general idea is similar to that from top to bottom, you can go directly to the code:

const int N = 510;
int f[N][N];
int a[N][N];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++) scanf("%d",&a[i][j]);
    for(int i=n;i>=1;i--)
        for(int j=1;j<=i;j++)
            f[i][j]=max(f[i+1][j]+a[i][j],f[i+1][j+1]+a[i][j]);
    printf("%d",f[1][1]);
    return 0;
}

 

Longest ascending subsequence

To tell you the truth, I feel the wonder of linear dp when I achieve the longest ascending subsequence. Linear dp just said that it is an equation of state with linear dp. The digital triangle just now may not be so obvious, so this problem can make us closer to the essence of linear dp.

Given a sequence of numbers with a length of ， N ， find the longest length of the subsequence with strictly monotonically increasing values.

When we see a dp problem, we must first think about its state representation. If we think in two dimensions: from ＾ i ＾ to ＾ j, the length of the ascending subsequence ending in j. If we think about it like this, we can find that ， i ， won't move, because even if you move, we find the longest, you still have to add the number in front of ， i ， so we can directly optimize it to one dimension and become the length of the ascending subsequence ending with ， j ，. With the status representation, how to update it? Because it is the longest, just take max directly.

int a[N],f[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];//Read in sequence
    for(int i=1;i<=n;i++)
    {
        f[i]=1;//Add only the number itself, which is a subsequence with length of 1
        for(int j=1;j<i;j++)
            if(a[i]>a[j])
            f[i]=max(f[i],f[j]+1);
    }
    int ans=0;
    for(int i=1;i<=n;i++)ans=max(ans,f[i]);
    cout<<ans;
    return 0;
}

However, if the data is a little larger, such as 100000, then our o (n^2) will run to the 10th power of 10 and must timeout. This kind of dp without optimization cannot pass. Is there any way to optimize? Indeed, there is. It can be optimized with dichotomy, but after optimization, it is not very like dp (the idea is changed from dp), so let it go for the time being, For the rising subsequence of big data, we'll talk about it later.

Longest common subsequence

Given two strings ＾ A ＾ and ＾ B with lengths ＾ N ＾ and ＾ M ＾ find the longest string length of both subsequences of ＾ A ＾ and ＾ B.

To tell you the truth, I haven't seen this kind of questions. The equation of state is really difficult to write, but recall the state representation of the longest ascending subsequence in the previous question: the length of the ascending subsequence ending in ， J ， is. Can we also write the state representation of this problem into two subsequences f [i] and f [J] ending with J and I respectively to represent its longest common subsequence? It may be possible, but if the two equations are written separately, it will be troublesome to update and difficult to compare. But our idea is right, so why not put them together? The state representation is still the longest common subsequence ending with J and ending with I, but the equation of state is no longer two one-dimensional, but becomes a two-dimensional f [i] [J]. In this way, it seems that there are a lot of cumbersome comparison steps, so that our focus falls on the two subsequences ending with I and j respectively.

After the state representation, the state calculation comes. Let's think about the state: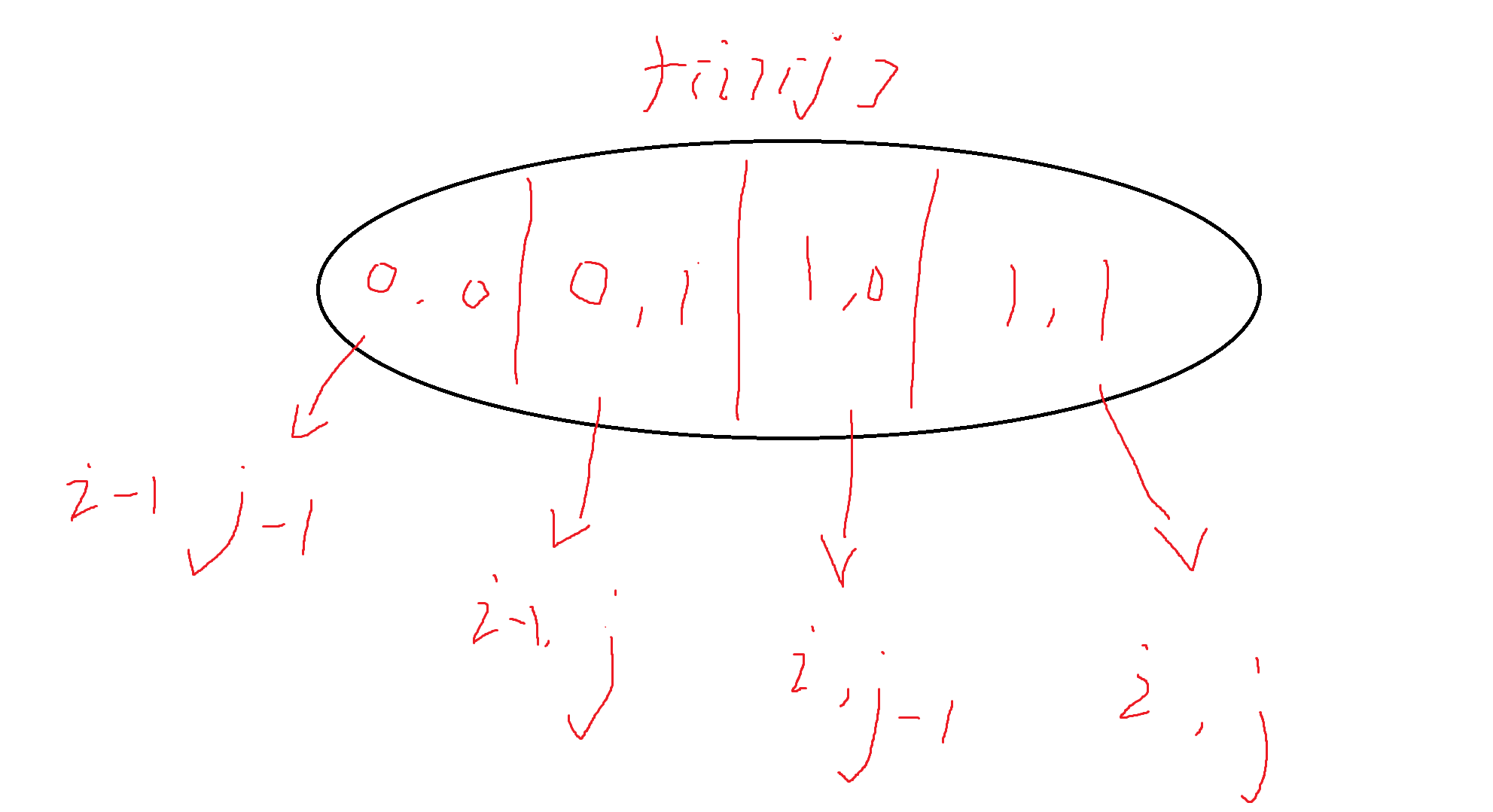

Here, 0 stands for no selection and 1 stands for selection - so we find that there are four states here, so we can take a max for these four states. In fact, it can be optimized here, because we still cover the first state when calculating the second and third States, so we can actually change to two or three, Four of these three states (state 4 exists only when I ending with and j ending with are equal, i.e. a[i]==b[j]):

const int N = 1010;

string a,b;
int f[N][N];
int n,m;

int main()
{
    cin>>n>>m>>a>>b;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);//2, Three states: max
            if(a[i-1]==b[j-1])f[i][j]=max(f[i][j],f[i-1][j-1]+1);//2, Max of three states and max of four states
        }
    cout<<f[n][m];
    return 0;
}

 

It y's too clear to sigh acwing Learn a little bit of experience, I hope it can help you (the set division of the longest common subsequence is learned from general y).