In my article a few days ago, I wrote about the operation and implementation of binary tree, but I haven't had the opportunity to brush OJ by myself. Today, he came and prepared several questions for your reference. Strengthen my knowledge and consolidate your understanding by the way. Do you kill two birds with one stone? Time is limited, I won't draw a picture to show it. You are so smart that you can understand it, right? I'll stay in the code for the general implementation idea. If necessary, friends can contact me for discussion!

Look down, the dry goods are all below~

1. Single valued binary tree

If each node of a binary tree has the same value, the binary tree is a single valued binary tree.
true is returned only when the given tree is a single valued binary tree; Otherwise, false is returned.

Tips:
The number of nodes in a given tree ranges from [1, 100].
The value of each node is an integer in the range of [0, 99].

//Realized by recursion
//If the val value is equal to the root - > val value, it is true
bool _isUnivalTree(struct TreeNode* root,int val){
    if(root == NULL)
        return true;
    if(val != root->val)
        return false;
    return _isUnivalTree(root->left,val) &&
           _isUnivalTree(root->right,val);
}
bool isUnivalTree(struct TreeNode* root){
    return _isUnivalTree(root,root->val);
}

2. Find the maximum depth of binary tree

Given a binary tree, find its maximum depth.
The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node.
Note: leaf nodes refer to nodes without child nodes

int maxDepth(struct TreeNode* root){
    //Air judgment
    if(root == NULL)
        return 0;
    //If it is not empty, the height is + 1 for the larger of the left and right subtrees
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return left > right ? left+1 : right+1;
}

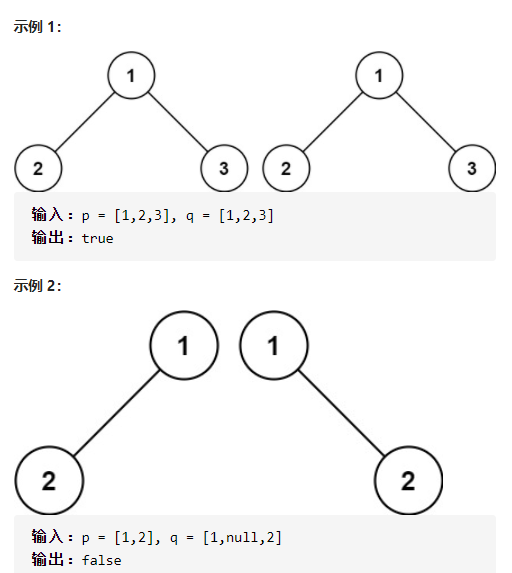
3. Judge whether it is the same tree

Give you the root nodes p and q of two binary trees and write a function to check whether the two trees are the same.
If two trees are structurally identical and the nodes have the same value, they are considered to be the same.

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    //Both trees are empty
    if(p == NULL && q == NULL)
        return true;
    //One tree is empty
    if(p == NULL || q == NULL)
        return false;
    //If none is empty, judge whether the node values at the same position of the two trees are equal and whether the nodes of the left and right children are the same
    return p->val ==q->val &&
    isSameTree(p->left,q->left) &&
    isSameTree(p->right,q->right);
}

4. Flip binary tree

Flip a binary tree.

struct TreeNode* invertTree(struct TreeNode* root){
    //Air judgment
    if(root == NULL)
        return NULL;
    //Swap the left and right child nodes of the root node
    struct TreeNode* tmp = root->left;
    root->left = root->right;
    root->right = tmp;
    //Recursion down until all are exchanged
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

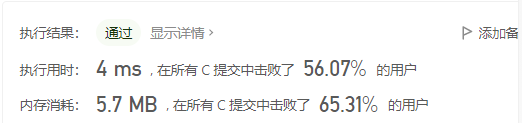
5. Symmetric binary tree

Given a binary tree, check whether it is mirror symmetric.

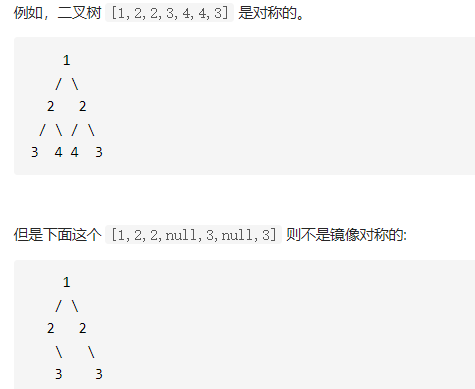
//This problem can be realized in this way
//You can copy this tree, and then recursively compare the root node and the left and right subtrees. If they are the same, they are symmetrical
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2)
{
	//If they are all empty, they are symmetrical
    if(root1 == NULL && root2 ==NULL)
    return true;
    //One is empty, asymmetric
    if(root1 == NULL || root2 ==NULL)
    return false;
    //Recursively compare the left subtree and the right subtree. If both meet the requirements, they will be symmetrical
    return root1->val==root2->val &&
     _isSymmetric(root1->right,root2->left) &&
    _isSymmetric(root1->left,root2->right);
}
bool isSymmetric(struct TreeNode* root){
    return _isSymmetric(root,root);
}

6. A subtree of another tree

Given two non empty binary trees s and T, check whether s contains subtrees with the same structure and node values as t. A subtree of s includes a node of S and all descendants of this node. S can also be regarded as a subtree of itself.

bool equal(struct TreeNode* s,struct TreeNode* t)
{
    //First, compare the root node. If the root node is empty at the same time, the two trees are equal.
    //If one of them is empty and the other is not empty, the two trees are unequal.
    //If the values on the nodes are not equal, the two trees are not equal.    
    if(!s &&!t)
        return true;
    if(s == NULL || t == NULL)
        return false;
    if(s->val != t->val)
        return false;
    //The values on the nodes are equal, and then compare whether their subtrees are equal downward. Use recursion to compare whether the left and right subtrees are equal. Note: they must be equal.
    return s->val == t->val &&
    equal(s->left,t->left) &&
    equal(s->right,t->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    //In the end of recursion, the root is empty, so there is no equality. return false;
    if(!root)
        return false;
    //Choose to go that way
    return equal(root,subRoot)||isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

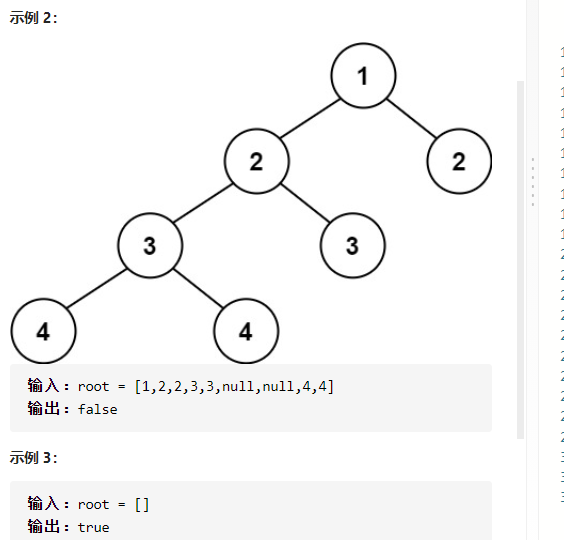
7. Judge whether it is a balanced binary tree

Given a binary tree, judge whether it is a highly balanced binary tree.
In this problem, a height balanced binary tree is defined as: the absolute value of the height difference between the left and right subtrees of each node of a binary tree does not exceed 1.

 //First find the depth (number of layers) of the tree
int height(struct TreeNode* root)
{
    if(root == NULL)
    { 
        return 0;
    }
    int left = height(root->left);
    int right =  height(root->right);
    return left > right ? left+1 : right+1;
}
//Top down, recursive
bool isBalanced(struct TreeNode* root){
    //An empty tree is a balanced binary tree
    if(root == NULL)
    {
        return true;
    }
    //All three conditions are met
    //The height difference between the left and right subtrees of the root node is no more than 1, and then go down recursively
    return fabs(height(root->left) - height(root->right)) <=1 &&
    isBalanced(root->left) &&isBalanced(root->right);
}

8. Traversal of binary tree

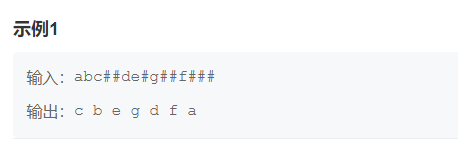
Make a program to read in a string of preorder traversal strings entered by the user, and establish a binary tree (stored in the form of pointer) according to this string. For example, the following pre order traversal string: ABC##DE#G##F#### where "#" represents a space, and the space character represents an empty tree. After the binary tree is established, the binary tree is traversed in middle order and the traversal result is output.

Enter Description:
The input includes 1 line of string, and the length does not exceed 100.
Output Description:
There may be multiple groups of test data. For each group of data, the output will be the sequence traversed in the middle order after the input string is established into a binary tree, and there is a space after each character. Each output result occupies one line.

#include<stdio.h>
#include<assert.h>
#include<malloc.h>
#include<string.h>
 
typedef struct TreeNode
{
    char data;
    struct TreeNode* left;
    struct TreeNode* right;
}TreeNode;
 
//Open up memory
TreeNode* BuyTreeNode(char ch)
{
    TreeNode* node=(TreeNode*) malloc(sizeof(TreeNode));
    if(node == NULL)
    {
        return NULL;
    }
 
    node->data = ch;
    node->left = node->right = NULL;
    return node;
}
 
//Create tree
TreeNode* TreeNodeCreate(char arr[],int size,int *index)
{
    TreeNode* root = NULL;
    if(*index < size && '#' != arr[*index])//Index is less than size and arr[*index] is not equal to ''#‘
    {
        root = BuyTreeNode(arr[*index]);//Create root node
        //Array goes back to create the left subtree
        (*index)++;
        root->left = TreeNodeCreate(arr, size, index);
        //Array goes back to create right subtree
        (*index)++;
        root->right = TreeNodeCreate(arr, size, index);
    }
    return root;
}
 
//Middle order traversal
void InorderTreeNode(TreeNode* root)
{
    if(root == NULL)
        return;
    InorderTreeNode(root->left);
    printf("%c ",root->data);
    InorderTreeNode(root->right);
}
 
//Destroy tree
void DestroyTree(TreeNode** root)
{
    if(*root)
    {
        DestroyTree(&(*root)->left);
        DestroyTree(&(*root)->right);
        free(*root);
        (*root) = NULL;
    }
  
}
 
int main()
{
    char arr[100];
    //Multi group input
    while(scanf("%s",arr) != EOF)
    {
        int index = 0;
        TreeNode* root = TreeNodeCreate(arr,strlen(arr),&index);
        InorderTreeNode(root);
        printf("\n");
        DestroyTree(&root);
    }
    return 0;
}

The above is the focus of this article. That's the end of today. Friends with different views or ideas are welcome to pay tribute to me. Based on the principle of mutual progress, I hope you can give me more opinions. Thank you~~