1. The concept of sorting
Sorting: the so-called sorting is the operation of arranging a series of records incrementally or decrementally according to the size of one or some keywords.
Stability: in the original sequence, r[i]=r[j], and r[i] is before r[j], but in the sorted sequence, r[i] is still before r[j], then this sorting algorithm is said to be stable; Otherwise, it is called unstable.

Internal sorting: load data into memory at one time.
External sorting: there are too many data elements to be placed in memory at the same time. According to the requirements of the sorting process, the sorting of data cannot be moved between internal and external memory.
2. Common sorting algorithms
2.1 insert sort – insert sort directly
Insertion of a single element
Given a group of elements [1, 2, 3, 4, 6, 7, 8, 9], insert 5 into this group of elements. First, insert it, which must meet that the original data has been arranged in sequence, and then compare it from back to front (in this way, the data can be moved back directly) for insertion. As shown below:
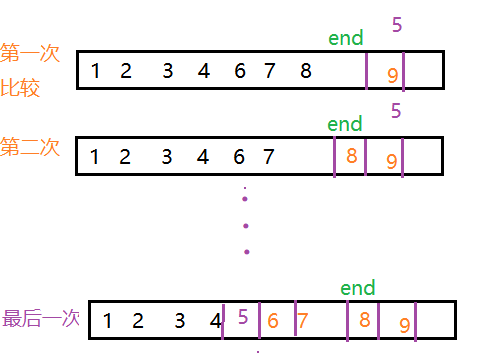
while(key<array[end]){
array[end+1]=array[end];
end--;
}
array[end+1]=key;
Now let's give a set of unordered data for quick sorting. The same principle as above, we can start from the second data of the data and compare it forward.
His time complexity is: O(N^2)
His stability: stable
Application scenario: the number of elements is small and close to order
for(int i=1;i<size;i++){
key=array[i];
int end=i-1;
while(end>=0&&key<array[end]){
array[end+1]=array[end];
end--;
}
array[end+1]=key;
}
Final realization:
void IsertSort(int array[], int size){
//Indicates the subscript of the current element to be inserted in the array. The element at i must be inserted before i
for (int i = 1; i < size; i++){
int key = array[i];//The element we want to insert starts with the i-th one
int end = i - 1;//end=i-1 of our array to be inserted
while (end>=0&&array[end]>key){
array[end + 1] = array[end];
end--;
}
array[end+1] = key;
}
}
2.2 insert sort – Hill sort
Now give a group of data, which is large and disordered. At that time, we still need to use the idea of insertion sorting. At this time, we can use Hill sorting.
Hill ranking method: also known as reduced incremental method. The basic idea of hill sorting method is to select an integer first, divide all records in the file to be sorted into groups, divide all records with distance into the same group, and sort the records in each group.
 How to group?
How to group?
At this time, we can group them at intervals. Suppose a mark gap=3 is given, and a subscript is divided into a group every 3 intervals for sorting.
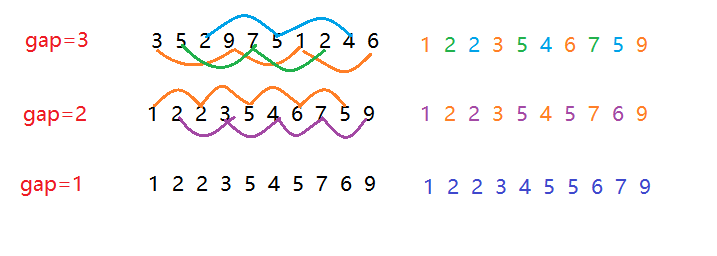
When gap > 1, it is pre sorted, which aims to make the array closer to order. When gap == 1, the array is close to ordered.
gap value:
int gap=size; gap=gap/3+1;
Complexity: O(N1.3-N2)
Stability: unstable
Application scenario: large amount of data and disorder.
void ShellSort(int array[], int size)
{
int gap = size;
while (gap > 0){
gap=gap/3+1;
for (int i = gap; i < size; i++){
int key = array[i];//The element we want to insert starts with the i-th one
int end = i - gap;//end=i-1 of our array to be inserted
while (end >= 0 && array[end]>key){
array[end + gap] = array[end];
end -= gap;
}
array[end + gap] = key;
}
}
}
2.3 select sort – select sort
Selective sorting: select the smallest (or largest) element from the data elements to be sorted each time and store it at the beginning of the sequence until all the data elements to be sorted are finished.
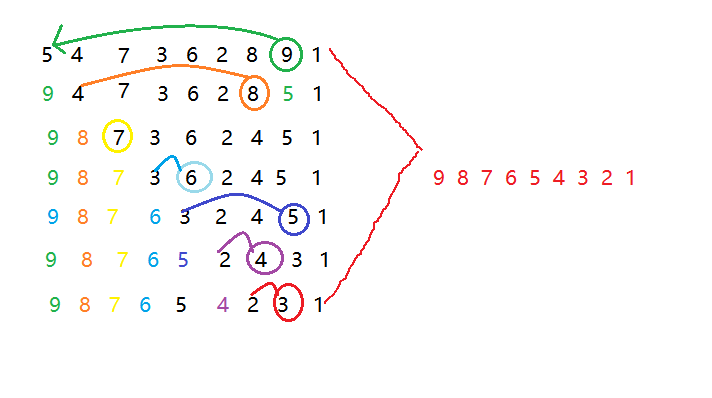
Time complexity: O(N^2)
Stability: unstable
//Descending sort
void SElectSort(int array[], int size){
for (int i = 0; i < size; i++){
int index = i;
int max = array[i];
for (int j = i; j < size; j++){
if (array[j]>max){
max = array[j];
index = j;
}
}
array[index] = array[i];
array[i] = max;
}
}
At the same time, the maximum and minimum values are arranged in descending order
//Adjust the maximum element and the minimum element at the same time
void SelectSorttogether(int array[], int size){
for (int i = 0; i < size; i++){
int max = array[i];
int min = array[size - i-1];
int index_max = i;
int index_min = size - 1 - i;
for (int j = i; j < size - i - 1; j++){
if (array[j]>max){
max = array[j];
index_max = j;
}
if (array[j] < min){
min = array[j];
index_min = j;
}
}
array[index_max] = array[i];
array[i] = max;
array[index_min] = array[size - i - 1];
array[size - i - 1] = min;
}
}
Defect in selecting sorting: duplicate comparison exists. – > How to optimize? Use heap sorting.
2.4 select sort – heap sort
(principle: My other blog)
void Heapadjustdown(int array[], int size, int parent){
int temp = 0;
int child = parent * 2 + 1;//Mark the left child first. There may not be another right child in a pile
while (child<size){//At this time, ensure that the parent node always has children
if (child + 1 < size&&array[child + 1] > array[child]){//At this time, first determine whether there is a right child and see whether the right child is larger than the left child
child += 1;//Mark child nodes
}
if (array[parent] < array[child]){
//If the parent node is smaller than the child node, then
temp=array[child] ;
array[child] = array[parent];
array[parent] = temp;
//At this time, after the exchange, adjust the position of its parent node and child node
parent = child;
child = parent * 2 + 1;
}
else{ break; }
}
}
//Heap sort
void Heapsort(int array[], int size){
int temp = 0;
//Build a pile, build a large pile in ascending order, and build a small pile in descending order
//Start from the penultimate non leaf node and adjust the position of the root node downward
int root = (size -1) / 2;
while (root >= 0)
{
Heapadjustdown(array, size, root);
root--;
}
//After downward adjustment, we can start to sort the heap by using heap deletion
int end = size-1;//Delete heap top element
while (end>0){
//1. Exchange heap top elements with heap tail elements
temp = array[0];
array[0]=array[end];
array[end] = temp;
//2. Delete the tail element
end--;
//3. Reorder the deleted heap downward
Heapadjustdown(array, end+1, 0);
}
}
2.5 swap sort – bubble sort
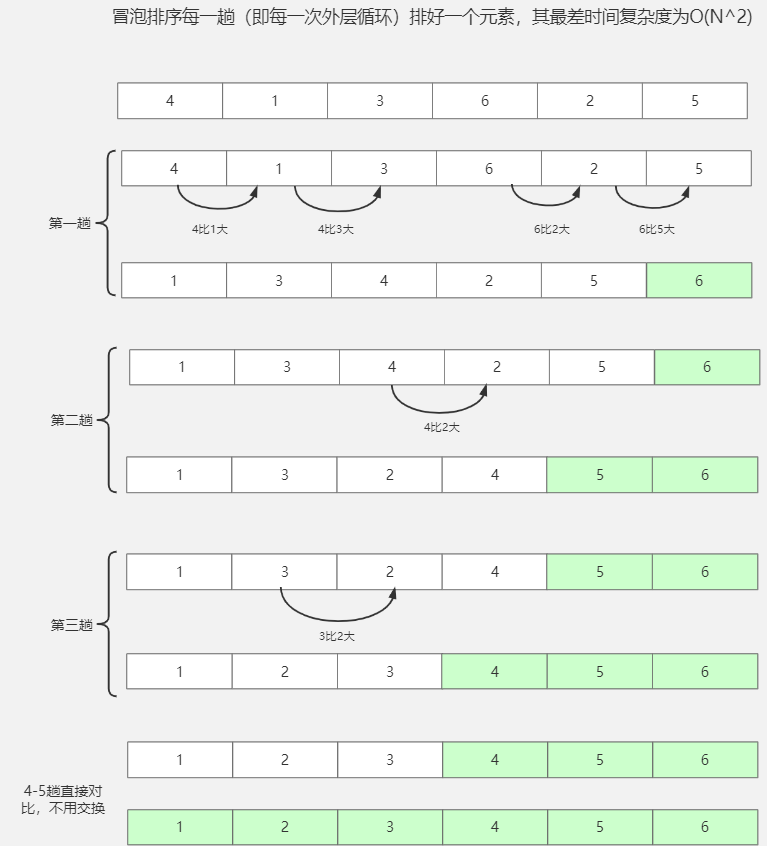
//Bubble sort
void BubbleSort(int array[], int size){
int swap = 0;
for(int i = 0; i < size-1; i++){
for (int j = 0; j < size - i-1; j++){
if (array[j]> array[j + 1]){
swap = array[j];
array[j] = array[j + 1];
array[j + 1] = swap;
}
}
}
}
2.6 exchange sort – quick sort
Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then repeat the process for the leftmost and leftmost subsequences until all elements are arranged in corresponding positions.

Now let's look at how to divide according to the benchmark value:
However, the selection of reference value is very important. In the selection of reference value, we should try to avoid selecting the maximum or minimum value in most cases. The following is the optimization of taking the reference value (three numbers take the middle method):
int middlenum(int array[], int left, int right){
int middle = (left + right) / 2;
if (array[left] < array[right]){
if (array[middle] < array[left])
return left;
else if (array[middle]>array[right])
return right;
else
return middle;
}
else{
if (array[middle]>array[left])
return left;
else if (array[middle] < array[right])
return right;
else
return middle;
}
}
Method 1: hoare
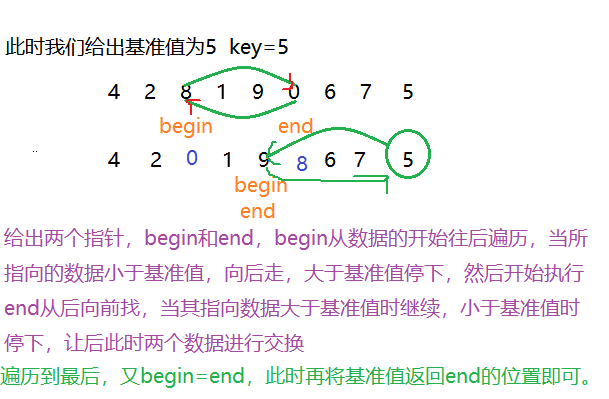
int partion1(int array[], int left1, int right1){
int left = left1;
int right = right1;
int temp = 0;
int key = middlenum(array,left,right);
//Exchange the positions of right and key, and put the reference value to the last position again
temp = array[right];
array[right] = array[key];
array[key] = temp;
while (right>left){
if (array[left]<array[right1]){
left++;
}
else{
if (array[right] >= array[right1]){
right--;
}
else{
temp = array[left];
array[left] = array[right];
array[right] = temp;
}
}
}
if (left < right1){
//Exchange the reference value at the left position
temp = array[right1];
array[right1] = array[left];
array[left] = temp;
}
return left;
}
Method 2: excavation method
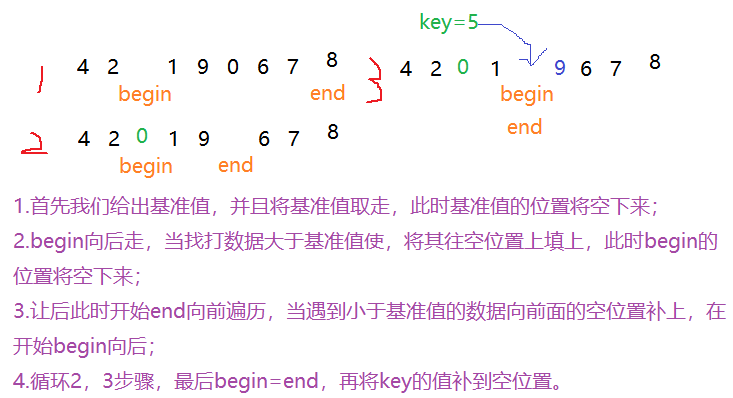
int partion2(int array[] , int left1, int right1){
//Excavation method
int left = left1;
int right = right1;
int temp = 0;
int key = middlenum(array, left, right);
//Exchange the positions of right and key, and put the reference value to the last position again
temp = array[right];
array[right] = array[key];
array[key] = temp;
int keynum = array[right1];//Save the key value
while (left < right){
while (left<right&&array[left] < keynum){
left++;
}
//If it is greater than, fill the pit with the data at this time
array[right] = array[left];
while (left<right&&array[right]>=keynum){
right--;
}
array[left] = array[right];
}
//Finally, the reference value is added to the empty position
array[left] = keynum;
return left;
}
Method 3: front and back pointer method

int partion3(int array[], int left, int right){
int cur = left;
int prve = cur - 1;
int key = middlenum(array, left, right);
//Exchange the positions of right and key, and put the reference value to the last position again
int temp = array[right];
array[right] = array[key];
array[key] = temp;
while (cur < right){
if (array[cur] < array[right] && ++prve != cur){
//Exchange the positions of right and key, and put the reference value to the last position again
temp = array[prve];
array[prve] = array[cur];
array[cur] = temp;
}
cur++;
}
if (++prve != right){
temp = array[prve];
array[prve] = array[right];
array[right] = temp;
}
return prve;
}
Implementation of quick sort:
1. Recursive method
void quickSort_hoare(int array[],int left,int right){
int div=0;
if (right - left < 1){
return;
}
//After that, we will sort the left side of the benchmark value and the right side
div = partion3(array, left, right);
//key left sorting
quickSort_hoare(array, left, div);
//Sort on the right of key
quickSort_hoare(array, div + 1, right);
}
2. Method of circulation
Because each recursion is equivalent to saving by pressing the stack layer by layer, we only need to define a stack structure and save the interval formed each time.
void QuicksortNor(int array[],int size){
stack s;
stackInit(&s);//Initialize stack
int left=0;
int right=size;
int div=0;
stackPush(&s,left);//Stack the left boundary
stackPush(&s,right);//Stack the right boundary
while(!StackEmpty(&s)){
right=stackTop(&s);//Take the right boundary element first
stackPop(&s);//remove
left=stackTop(&s);
stackPop(&s);
if(right-left>=1){
div=pation1(array,left,right);
//[div + 1, right], press the right half first
stackpush(&s,div+1);
stack(&s,right);
//[left,div]
stackpush(&s,left);
stackpush(&s,div);
}else{
break;
}
}
stackDestory(&s);//Stack destruction
}
Fast scheduling time complexity – O(Nlog2(N)) in the best case and – O(N^2) in the worst case.
The best space complexity is – O(log2N), and in the worst case – O(N).
2.7 merge sort
The quantity is too large to be loaded into memory at one time.
1. In learning merging and sorting, we need to know that given two groups of ordered data, we can combine them into one group of data.
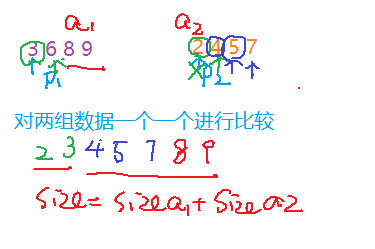
void meraedata(int array[],int left,int right,int temp[]){
//Now, we always use [left, mid] for one group of data and [mid right] for the other group of data
int i = 0;
int begin1 = left;
int end1 = left + (right - left) / 2;
int begin2 = end1+1;
int end2= right;
//Merge
while (begin1 <= end1&&begin2 <= end2){
if (array[begin1] < array[begin2]){
temp[i++] = array[begin1];
begin1++;
}else{
temp[i++] = array[begin2];
begin2++;
}
}
while (begin1 <= end1){
temp[i++] = array[begin1++];
}
while (begin2 < end2){
temp[i++] = array[begin2++];
}
}
2. Principle: first divide in return
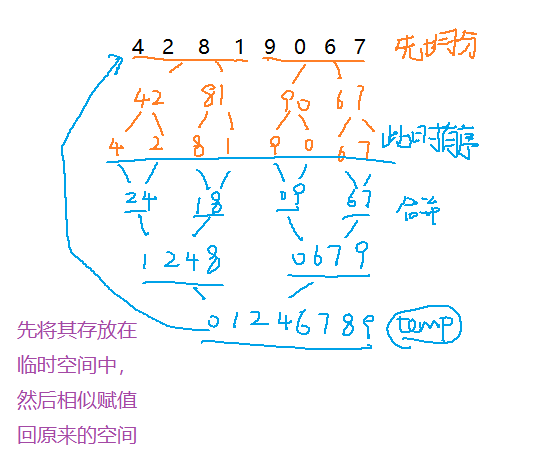
//Merge sort
void meraedata(int array[], int left, int mid, int right, int temp[]){
//Now, we always use [left, mid] for one group of data and [mid+1,right) for the other group of data
int begin1 = left;
int end1 = mid;
int begin2 = mid;
int end2 = right;
int i = left;
//Merge
while (begin1 < end1&&begin2 < end2){
if (array[begin1] <= array[begin2]){
temp[i++] = array[begin1++];
}
else{
temp[i++] = array[begin2++];
}
}
while (begin1 < end1){
temp[i++] = array[begin1++];
}
while (begin2 < end2){
temp[i++] = array[begin2++];
}
}
void _mergesort(int array[], int left, int right, int temp[]){
if (right - left <= 1)
return;
int mid = left + ((right - left)>>1);
//Advanced line classification
_mergesort(array, left, mid, temp);
_mergesort(array, mid, right, temp);
//Then sort and merge the divided data
meraedata(array, left, mid, right, temp);
//Then copy it back
memcpy(array + left, temp + left, sizeof(array[0] * (right - left)));
}
void mergesort(int array[], int size){
int *temp = (int *)malloc(sizeof(array[0])*size);
if (NULL == temp) return;
_mergesort(array, 0, size, temp);
free(temp);
}
2.8 non comparative sorting
Sequence: data intensive exists in the range of 0-9
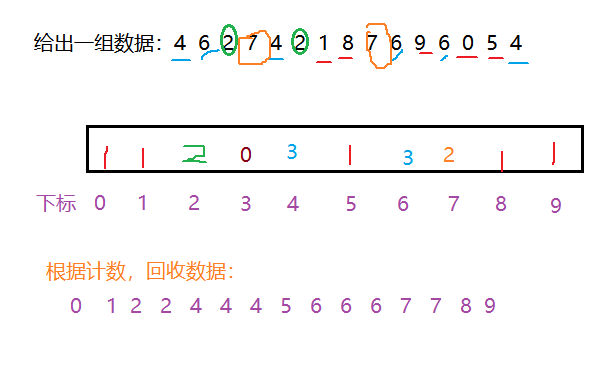
1. Count the number of occurrences of each element;
2. According to the counting results, recycle from small to large according to the subscript of the counting array;
//Suppose we don't tell the range of this set of data here
void countSort(int array[], int size){
//Therefore, we need to count the data range and traverse it once
int num = 0;
int max = array[0];
int min = array[0];
for (int i = 1; i < size; i++){
if (array[i]>max)
max = array[i];
if (array[i] < min)
min = array[i];
}
int range = max - min + 1;//Find the maximum space of the array
int* count = (int*)calloc(range, sizeof(int)*range);
for (int i = 0; i < size; i++){//Count each data in the original array
count[array[i] - min] += 1;
}
for (int i = 0; i < range; i++){//Then re output it
for (int j = 0; j < count[i]; j++){
array[num++] = i + min;
}
}
free(count);
}