catalogue
1. Mystery of the future
/**In 2022, Mike found two binary integers a and B with length n (both of which are only represented by the numbers 0 and 1), and the leading can have 0. In order not to forget them, he wants to construct the integer d in the following way:
He creates an integer c as the result of the bit sum of a and b. there is no carry transfer, so c may have one or more 2's. For example, the result of bitwise summation of 0110 and 1101 is 1211, or the sum of 011000 and 011000 is 022000;
Mike replaces the equal consecutive numbers in c with 1 bit to get d. In the above case, after this operation, 1211 becomes 121022000 and 020 (so d has no equal continuous number).
Unfortunately, Mike lost the integer a before he calculated d himself. Now, to cheer him up, you have to find any binary integer of length n, a, with D as the maximum value of the integer.
The maximum possible integer indicates 102 > 21012 < 101021 = 21, and so on.
input
The first line contains a single integer t(1 ≤ t ≤ 1000) - the number of test cases.
The first line of each test case contains the length of integers n(1 ≤ n ≤ 10^5) a and b.
The second line of each test case contains a binary integer b of length n. The integer b consists only of the numbers 0 and 1.
It ensures that the sum of n to all t test cases does not exceed 10 ^ 5.
output
For each test case, output a binary integer a with length n. Note that a or b can have a leading 0, but must have the same length n.
Please note that
In the first test case, b=0, select a=1, and the result is d=1.
In the second test case, b=011, so:
If a=000, c = 011, then d=01;
If a=111, c = 122, then d=12;
If you choose a=010, you get d=021.
If you choose a=110, you will get d=121.
We can prove that the answer a=110 is optimal and d=121 is the most possible.
In the third test case, b=110. If you choose a=100, you get d=210, which is the maximum value of D.
In the fourth test case, b=111000. If you choose a=101101, you will get d=212101, which is the most possible D.
In the fifth test case, b=001011. If you choose a=101110, you will get d=102121, which is the most possible D*/
thinking
Pay attention to the combined numbers. If the adjacent two numbers are the same, they will be merged, and each digit of A is composed of 0 or 1. To make C the largest, the first digit is taken as 1, and the following digits are taken as large as possible, and ensure that they are not repeated with the previous digit.
Code display
#include<stdio.h>
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
getchar();
int i,b=0,a[100005]={0};
while((a[b]=getchar())!='\n')
b+=1;
printf("1");
a[0]++;
for(i=1;i<b;i++)
{
if(a[i-1]=='2')
{
if(a[i]=='1')
printf("0");
else{
printf("1");
a[i]++;
}
}
else if(a[i-1]=='1')
{
if(a[i]=='1')
{
a[i]++;
printf("1");
}
else
printf("0");
}
else
{
printf("1");
a[i]++;
}
}printf("\n");
}
return 0;
}2. Don't be distracted
/*Polycarp has 26 tasks. Each task is designated by a capital letter of the Latin alphabet.
The teacher asked Polycarp to solve tasks in the following way: if Polycarp began to solve some task, then he must solve it to the end, without being distracted by another task. After switching to another task, Polycarp cannot return to the previous task.
Polycarp can only solve one task during the day. Every day he wrote down what task he solved. Now the teacher wants to know if Polycarp followed his advice.
For example, if Polycarp solved tasks in the following order: "DDBBCCCBBEZ", then the teacher will see that on the third day Polycarp began to solve the task 'B', then on the fifth day he got distracted and began to solve the task 'C', on the eighth day Polycarp returned to the task 'B'. Other examples of when the teacher is suspicious: "BAB", "AABBCCDDEEBZZ" and "AAAAZAAAAA".
If Polycarp solved the tasks as follows: "FFGZZZY", then the teacher cannot have any suspicions. Please note that Polycarp is not obligated to solve all tasks. Other examples of when the teacher doesn't have any suspicious: "BA", "AFFFCC" and "YYYYY".
Help Polycarp find out if his teacher might be suspicious.
Input
The first line contains an integer t (1≤t≤1000). Then t test cases follow.
The first line of each test case contains one integer n (1≤n≤50) — the number of days during which Polycarp solved tasks.
The second line contains a string of length n, consisting of uppercase Latin letters, which is the order in which Polycarp solved the tasks.
Output
For each test case output:
"YES", if the teacher cannot be suspicious;
"NO", otherwise.
You may print every letter in any case you want (so, for example, the strings yEs, yes, Yes and YES are all recognized as positive answer).
Example
input
5
3
ABA
11
DDBBCCCBBEZ
7
FFGZZZY
1
Z
2
AB
output
NO
NO
YES
YES
YES*/
thinking
It is needless to say whether the string appears repeatedly
Code display
#include <stdio.h>
#include <string.h>
int main()
{
char a[1001];
int b[1001] = {0};
int n, i, j, k, len;
scanf("%d", &n);
for (i = 0; i < n; i++) {
scanf("%d", &len);
scanf("%s", a);
for (j = 0; j < len; j++) {
if (a[j] != a[j - 1]) {
for (k = 0; k < j; k++) {
if (a[k] == a[j]) {
b[i] = 1;
break;
}
}
}
if (b[i] == 1)
break;
}
}
for (i = 0; i < n; i++) {
if (b[i] == 0)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}3. River crossing pawn

thinking
Mark the horse and the place where the horse can reach, then update the coordinates in order, a[x,y]=a[x-1,y]+a[x,y-1], and finally output the value of a[x,y].
Code display
#include<stdio.h>
int main()
{
int x1,x2,y1,y2;
long long int a[30][30];
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
//All positions that cannot be passed
a[x2][y2]=-1;
if(y2-2>=0 && x2+1<=x1)
a[x2+1][y2-2]=-1;
if(y2-2>=0 && x2-1>=0)
a[x2-1][y2-2]=-1;
if(y2-1>=0 && x2+2<=x1)
a[x2+2][y2-1]=-1;
if(y2-1>=0 && x2-2>=0)
a[x2-2][y2-1]=-1;
if(y2+1<=y1 && x2+2<=x1)
a[x2+2][y2+1]=-1;
if(y2+1<=y1 && x2-2>=0)
a[x2-2][y2+1]=-1;
if(y2+2<=y1 && x2+1<=x1)
a[x2+1][y2+2]=-1;
if(y2+2<=y1 && x2-1>=0)
a[x2-1][y2+2]=-1;
for(int i=1;i<=x1;i++)
{
if(a[0][i]==-1)
{
for(int j=i+1;j<=y1;j++)
{
if(a[0][j]!=-1)
a[0][j]=0;
}
break;
}else{
a[0][i]=1;
}
}
for(int i=1;i<=y1;i++)
{
if(a[i][0]==-1)
{
for(int j=i+1;j<=x1;j++)
{
if(a[j][0]!=-1)
a[j][0]=0;
}
break;
}else{
a[i][0]=1;
}
}
for(int i=1;i<=x1;i++)
for(int j=1;j<=y1;j++)
{
if(a[i][j]!=-1)
{
if(a[i-1][j]==-1&&a[i][j-1]==-1){
a[i][j]=0;
}else if(a[i-1][j]==-1&&a[i][j-1]!=-1){
a[i][j]=a[i][j-1];
}else if(a[i-1][j]!=-1&&a[i][j-1]==-1){
a[i][j]=a[i-1][j];
}else if(a[i-1][j]!=-1&&a[i][j-1]!=-1){
a[i][j]=a[i][j-1]+a[i-1][j];
}
}
}
printf("%lld\n",a[x1][y1]);
return 0;
}#include<stdio.h>
long long dp[30][30];
int main()
{
int n,m,a,b,i,j;
scanf("%d%d%d%d",&a,&b,&n,&m);
m++;n++;a++;b++;
for(i=1;i<=a;i++)
for(j=1;j<=b;j++)
{
if(i==1 && j==1)
dp[i][j] = 1;
else if((i==n&&j==m) || (i==n-1&&j==m-2) || (i==n-2&&j==m-1) || (i==n-2&&j==m+1) || (i==n-1&&j==m+2) || (i==n+1&&j==m+2) || (i==n+2&&j==m+1) || (i==n+2&&j==m-1) || (i==n+1&&j==m-2))
dp[i][j]=0;
else if(i!=1 || j!=1)
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
printf("%lld\n",dp[a][b]);
return 0;
} 4. Carpet
thinking
1. Three cycles of brute force cracking, in the covered area + 1
2. First two-dimensional difference, then two-dimensional prefix and
Code display
Three cycles of brute force cracking (timeout if there is no accident)
#include <stdio.h>
int a[1001][1001] = {0};
int main() {
int x1, y1, x2, y2;
int n, m;
scanf("%d %d", &n, &m);
for (int i=1;i<=m;i++) {
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
for(int j=x1;j<=x2;j++)
for(int k=y1;k<=y2;k++)
{
a[j][k]++;
}
}
for (int i=1;i<=n;i++) {
for (int j=1;j<=n;j++) {
printf("%d ",a[i][j]);
}
printf("\n");
}
return 0;
}Prefix and
#include<stdio.h>
int a[1005][1005]={0};
int main()
{
int n,m,x1,x2,y1,y2;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
for(int j=x1;j<=x2;j++)
{
a[j][y1]+=1;
a[j][y2+1]-=1;
}
}
for(int i=1;i<=n;i++)//Each line
{
for(int j=1;j<=n;j++)//Each column
{
a[i][j]+=a[i][j-1];//Prefix and
}
}
//Output operation
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
-printf("%d ",a[i][j]);
}
printf("\n");
}
return 0;
}5. Minimum new integer
/*Given a decimal positive integer n (0 < n < 1000000000), the number on each digit is not 0. The number of digits of n is m.
Now delete the k-bit (0 < K < m) (0 < K < m) from the m-bit, and find the minimum value of the generated new integer?
For example: n=9128456,k=2, the minimum new integer generated is 12456.
Input format
The first row, t, indicates that there are t groups of data;
Next, line t, each line represents a set of test data, and each set of test data contains two numbers n,k.
Output format
Line t, one number per line, represents the smallest integer obtained after deleting k bits from n.
Sample Input
2
9128456 2
1444 3
Sample Output
12456
1*/
thinking
Note: delete the number that is higher and greater than or equal to the number behind it
To delete the number larger than the latter, rather than the largest number, for example, 1329 1, 132 must be larger than 129. If the number has grown from small to large, delete it from back to front until k bits are deleted
Code display
#include <stdio.h>
#include <string.h>
int main()
{
char n[50];
int t,k,len,flag=1;
scanf("%d",&t);
while(t--){
scanf("%s %d",n,&k);
len=strlen(n);
for(int i=0;i<k;i++){
for(int j=0;j<len-1;j++){
if(n[j]>n[j+1]){
for(int l=j;l<len-1;l++){//Move forward and overwrite the large ones, which is equivalent to deletion
n[l]=n[l+1];
}
break;
}
}
len--;//The length is reduced by 1 each time. If it grows from small to large, the last digit is deleted directly
}
for(int i=0;i<len;i++){
printf("%c",n[i]);
}
printf("\n");
}
}
6. Astronauts
Problem Description:
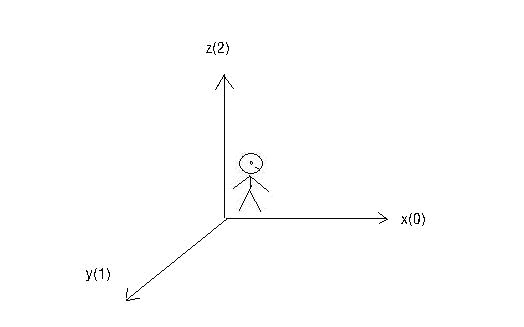
The astronaut lost his way in space. Now a virtual xyz coordinate system is established at his starting position, which is called the absolute coordinate system. The direction of the front of the astronaut is the positive direction of the x-axis and the direction of the top of the head is the positive direction of the z-axis. The initial state of the astronaut is shown in the following figure:
Now the six directions are labeled respectively. The positive directions of x, y and z are 0, 1 and 2 respectively, and the negative directions are 3, 4 and 5 respectively; Call them absolute directions. An astronaut walks in the universe only in a direction parallel to the xyz axis of the absolute coordinate system, but he does not know his current absolute coordinate and the absolute direction he faces.
Task description:
Please determine the final absolute coordinates and the absolute direction of the astronauts according to the astronauts' description of their movement in the relative direction. The description and significance of moving in the relative direction are as follows:
Forward x go forward x meters.
back x turn first and then walk x meters.
left x turn left first and then walk x meters.
right x turn right first and then walk x meters.
up x face up first, then walk x meters.
down x face down first, then walk x meters.
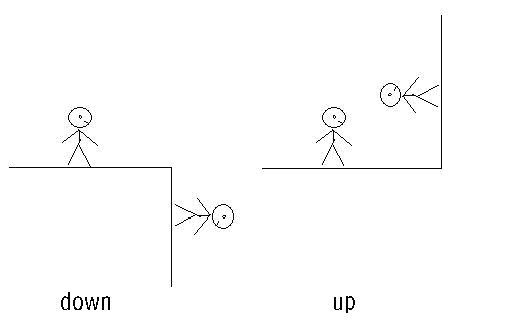
Up and down are shown in the figure below:
Input
The first line is a positive integer m, which represents the number of groups of test data. The first row of each group of test data is a positive integer, n (1 < = n < = 10000) represents the number of astronauts walking, and the following n rows enter a relative walk for each row, with the format as described above, where (1 < = x < = 10000 is a positive integer).
Output
For each set of input data, output a line, x y z p, separated by a space, x y z is the absolute coordinate of the astronaut's position, and p is the absolute direction number facing the astronaut (0 < = p < = 5).
Sample
| Inputcopy | Outputcopy |
|---|---|
1 6 left 10 right 11 up 12 down 13 forward 14 back 15 | 23 -10 12 3 |
thinking
When climbing up, the direction of the face is the same as that of the original head, so lian=tou. At this time, the direction of the head is (the direction of the original lian + 3)% 6;
When climbing down, the direction of the head is the direction of the original lian, so tou=lian. At this time, the direction of lian is (the direction of the original tou + 3)% 6;
When climbing to the left, lian's direction is the direction of the original zuo's hand, so lian=zuo. At this time, Zu's direction is (original lian's direction + 3)% 6;
When climbing to the right, the direction of zuo is the direction of the original lian, so zuo=lian. At this time, the direction of lian is (the direction of the original Zu + 3)% 6;
When returning, the direction of the Zu is (original Zu + 3)% 6. At this time, the direction of lian is (the original direction of lian + 3)% 6;
Code display
#include<stdio.h>
#include<string.h>
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
char s[10];
int a;
int x=0,y=0,z=0;
int lian=0,zuo=4,tou=2;//Original direction
int t;
for(int i=0;i<n;i++)
{
scanf("%s%d",s,&a);
if(s[0]=='l')
{
t=lian;
lian=zuo;
zuo=(t+3)%6;
}
else if(s[0]=='r')
{
t=zuo;
zuo=lian;
lian=(t+3)%6;
}
else if(s[0]=='u')
{
t=lian;
lian=tou;
tou=(t+3)%6;
}
else if(s[0]=='d')
{
t=tou;
tou=lian;
lian=(t+3)%6;
}
else if(s[0]=='b')
{
zuo=(zuo+3)%6;
lian=(lian+3)%6;
}
if(lian==0)
{
x+=a;
}
else if(lian==1)
{
y+=a;
}
else if(lian==2)
{
z+=a;
}
else if(lian==3)
{
x-=a;
}
else if(lian==4)
{
y-=a;
}
else if(lian==5)
{
z-=a;
}
}
printf("%d %d %d %d\n",x,y,z,lian);
}
}