I Title Description

Give you a binary matrix grid of size m x n.
Islands are a combination of adjacent ones (representing land). The "adjacent" here requires that two ones must be adjacent in four horizontal or vertical directions. You can assume that all four edges of the grid are surrounded by 0 (representing water).
The area of an island is the number of cells on the island with a value of 1.
Calculate and return the largest island area in the grid. If there are no islands, the return area is 0.

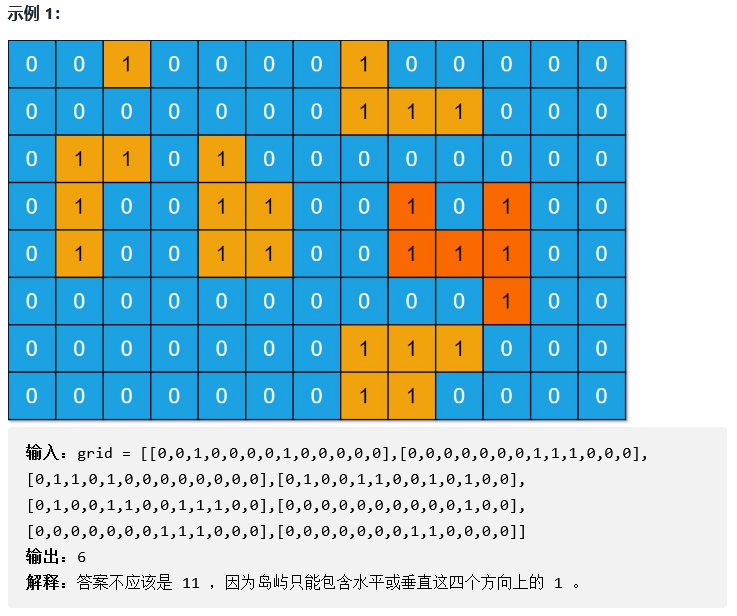
II Detailed explanation of depth first search and breadth first search

1. Depth first search

First, let's learn about depth first search, that is, starting from a head node, access the next node connected to the head node according to a certain data structure, and then access a node connected to the current node from the next node. Cycle back until the accessed current node has no next connected node, and start to trace back to the previous node of the current node, Repeat the access operation on the premise that the above node is the starting node, and keep backtracking until all nodes are accessed.
Note: after visiting a land node, be sure to set the visited node to 0, otherwise the land area will be calculated repeatedly because each block of the map will be used as a starting node
If we explore each land connected to it in four directions on a land (and the land connected to these lands), the total amount of land explored will be the area of the connected shape.

//Traverse every piece of the map
	 public static int maxAreaOfIsland(int[][] grid) {
		 int area=0;    //The initial area is set to 0
		 //Visit each grid. Take each grid as a starting node and visit in four directions up, down, left and right. The sum of all connected nodes in four directions is 1, which is the area of the small island
		 for(int i=0;i<grid.length;i++) {
			 for(int j=0;j<grid[0].length;j++) {
				 area=Math.max(area, maxArea(i,j,grid));  //The largest island area is obtained by recursive comparison
			 }
		 }
		 return area;
	 }

	public static int maxArea(int x, int y,int[][] grid) {
		//Ensure that the node is legal to prevent the array from crossing the boundary, and if the node is 1, it is land
		if(x>=0&&x<grid.length&&y>=0&&y<grid[0].length&&grid[x][y]==1) {
			grid[x][y]=0;   //Set the visited land to 0 to prevent repeated visits
			//Return all land areas in the four directions up, down, left and right of the node
			return 1+maxArea(x+1, y, grid)+maxArea(x-1, y, grid)+
					maxArea(x, y-1, grid)+maxArea(x, y+1, grid);
		}else{
			return 0;
		}
	}

2. Breadth first search

The simple understanding of breadth first search is that starting from the starting node, first put all the nodes connected to the starting node into the queue, then take out the head node of the queue, add all the unreachable nodes connected to the node to the tail of the queue, and then take out the current head node of the queue, and repeat until the queue is empty, that is, all nodes have been accessed.
Visit the starting land and add the land to be traversed next (i.e. the land connected with the four directions of the starting land) to the tail of the team. Each time the land is taken out from the head of the team, the breadth first search algorithm is realized.

public static int maxAreaOfIsland(int[][] grid) {
		int area=0;
		for(int i=0;i<grid.length;i++) {
			for(int j=0;j<grid[0].length;j++) {
				if(grid[i][j]==1) {
					area=Math.max(area, bfs(grid,i,j));
				}
			}
		}
		return area;
	}
	
	public static int bfs(int grid[][],int i,int j) {
		Queue<int[]> queue=new LinkedList<int[]>();  //Create queue
		queue.offer(new int[] {i,j});  //Adds an array of locations to the queue as the starting node
		grid[i][j]=0; //The queued node (accessed) is marked as 0
		int area=1;  //Because there is at least one piece of land, the initial value of area is set to 1	
		int[] queuei= {0,0,1,-1};
		int[] queuej= {1,-1,0,0};
		
		while(!queue.isEmpty()) {
			int[] tem=queue.poll(); //First element out of queue
			int x=tem[0],y=tem[1]; //Starting node location
			//Add all land nodes connected with {x,y} nodes to the tail of the team
			for(int k=0;k<4;k++) {
				int nx=x+queuei[k],ny=y+queuej[k];
				if(nx>0&&nx<grid.length&&ny>0&&ny<grid[0].length&&grid[nx][ny]==1) {
					queue.offer(new int[] {nx,ny});
					grid[nx][ny]=0;
					area++;
				}
			}	
		}
		return area;
	}