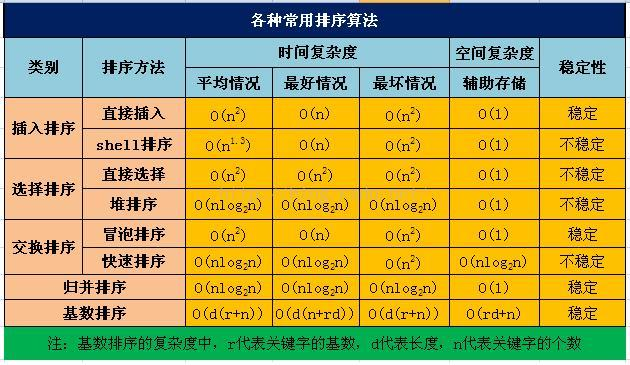
Sorting can be divided into two categories: internal sorting and external sorting. In the sorting process, all records are stored in memory, which is called internal sorting. If external memory needs to be used in the sorting process, it is called external sorting. The sorting mentioned below belongs to internal sorting.  

1, Insert sort

(1) , direct insert sort

public class Sort {
    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = insertionSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    /**
     * Use a temporary variable to store the value to be inserted. Look from the back to the front. If an element larger than this value is found, move the elements in front of it back in turn,
     * After that, put the value with insertion into the position of the insertion, subtracting many unnecessary exchange operations
     * @param arr
     * @return
     */
    public static int[] insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            //Element to be inserted
            int insertValue = arr[i];
            int preIndex = i - 1;
            while (preIndex >= 0 && insertValue < arr[preIndex]) {
                arr[preIndex + 1] = arr[preIndex];
                preIndex--;
            }
            arr[preIndex + 1] = insertValue;
        }
        return arr;
    }
}

(2) , Hill sort (shell sort)

public class Sort {
    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = shellSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    /**
     * Shell Sort 
     * Insert an upgraded version of sorting, set the step size to half the length of the array, and divide by two each time until the step size is 1
     * @param arr
     * @return
     */
    public static int[] shellSort(int[] arr) {
        int len = arr.length;
        for (int k = len / 2; k > 0; k /= 2) {
            for (int i = k; i < len; i++) {
                int temp = arr[i];
                int j = i - k;
                while (j >= 0 && temp < arr[j]) {
                    arr[j + k] = arr[j];
                    j -= k;
                }
                arr[j + k] = temp;
            }
        }
        return arr;
    }
}

2, Select sort

(1) . simple selection sorting (direct sorting)

public class Sort {
    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = selectionSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    /**
     * Traverse the array, find the smallest element every time, record its subscript, and exchange it with the array header element according to the subscript after the inner loop
     * Unlike bubbling sort, bubbling sort may be exchanged multiple times per cycle, while selective sort can be exchanged at most once
     * @param arr Array to be sorted
     * @return
     */
    public static int[] selectionSort(int[] arr) {
        int temp, minIndex;
        for (int i = 0; i < arr.length - 1; i++) {
            minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
        return arr;
    }
}

(2) , heap sort

public class HeapSort {

    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = heapSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    public static int[] heapSort(int[] arr) {
        //Build a large top heap with the last non leaf node
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            adjustHeap(arr, i, arr.length);
        }
        //At this time, the top element is the largest, and the top element and end element are exchanged
        for (int i = arr.length - 1; i > 0; i--) {
            swap(arr, 0, i);
            //The end element is already the largest, and there is no need to consider sorting
            adjustHeap(arr, 0, i);
        }
        return arr;
    }

    /**
     * Form a large top pile
     *
     * @param arr Array element
     * @param i   Current node location
     * @param len Number of nodes
     */
    public static void adjustHeap(int[] arr, int i, int len) {
        //Save current node
        int temp = arr[i];
        //Traverse the left child node of the current node
        for (int k = 2 * i + 1; k < len; k = 2 * k + 1) {
            //If the right node exists and the right node is larger than the left node, point to the right node
            if (k + 1 < len && arr[k] < arr[k + 1]) {
                k++;
            }
            //Judge which node is larger than the current node and the left (right) node
            if (temp < arr[k]) {
                //exchange
                swap(arr, k, i);
                //After the exchange, the next traversal of the subtree with this child node as the root node will be affected, so it is necessary to reassign the next root node
                i = k;
            } else {
                //No exchange, just terminate the loop
                break;
            }
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

3, Exchange sort

(1) Bubble sort

/**
 * Traverse the array, compare and exchange adjacent elements in turn, and put the largest element (determined according to positive or reverse order) at the end of the array each time
 * @param arr Array to be sorted
 * @return
 */
public static int[] bubbleSort(int[] arr) {
    int temp;

    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j + 1];
                arr[j + 1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

Bubble sorting optimization I:

//Bubble sorting: optimization I
public static int[] bubbleSort1(int[] arr) {
    int temp;
    //Is the record array ordered
    boolean isSorted;

    for (int i = 0; i < arr.length - 1; i++) {
        isSorted = true;
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j + 1];
                arr[j + 1] = arr[j];
                arr[j] = temp;
                //Record whether the elements have been exchanged in this round of sorting. If so, set to false
                isSorted = false;
            }
        }
        //No exchange proves that it is already ordered. Directly terminate the loop
        if (isSorted) {
            break;
        }
    }
    return arr;
}

Bubble sorting optimization II:

//Bubble sorting: optimization II
public static int[] bubbleSort2(int[] arr) {
    int temp;
    boolean isSorted;
    //First cycle boundary
    int sortBorder = arr.length - 1;
    //Record the position of the last exchange in each round of sorting
    int lastSwapIndex = 0;

    for (int i = 0; i < arr.length - 1; i++) {
        isSorted = true;
        for (int j = 0; j < sortBorder; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j + 1];
                arr[j + 1] = arr[j];
                arr[j] = temp;
                isSorted = false;
                lastSwapIndex = j;
            }
        }
        sortBorder = lastSwapIndex;
        if (isSorted) {
            break;
        }
    }
    return arr;
}

(2) , quick sort

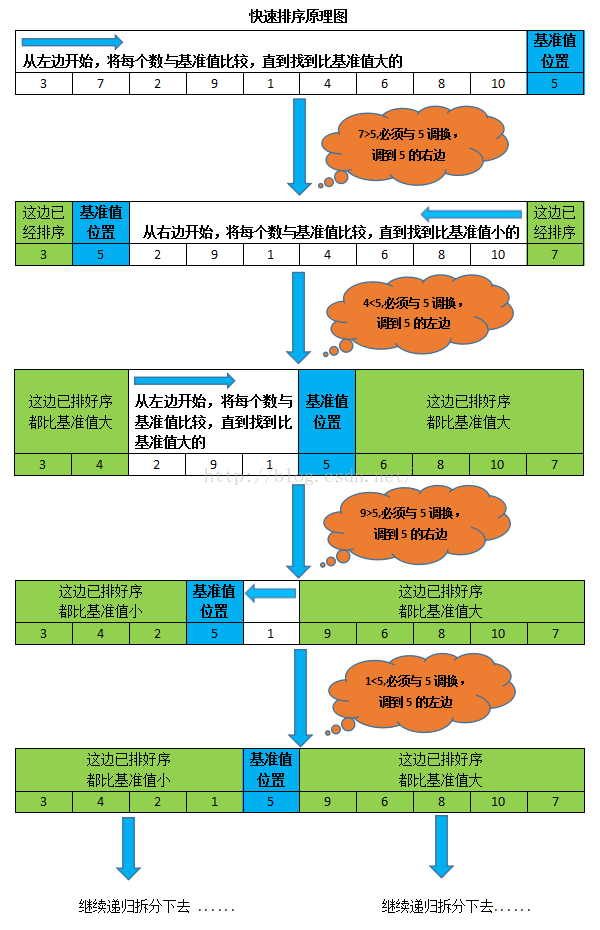
Algorithm principle: first select a number in the array, and divide the data to be sorted into two independent parts through one sorting: the numbers smaller than the selected number are moved to the left of the array, and the numbers larger than the selected number are moved to the right of the array. Then quickly sort the two parts of data according to this method, and the whole sorting process can be recursive, so as to turn the whole data into an ordered sequence.

Benchmark selection in quick sort:
1. The first element or the last element, but when the elements in the array are originally in reverse order, the ascending sorting will only determine the position of the reference element at one time, which can not give full play to the advantage of fast sorting
2. Random selection
3. Three numbers take the middle method, that is, take the left, middle and right numbers, and then sort them, taking the middle number as the hub value.

Take chestnuts for example:

Original array: {3, 7, 2, 9, 1, 4, 6, 8, 10, 5}
Expected results: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Quick sort diagram:

Code implementation:

public class QuickSort {
    
    public static int divide(int[] a, int start, int end){
        //The rightmost element is used as the reference value each time
        int base = a[end];
        //start Once equal to end，It means that the left and right pointers are merged to the same position, which can end this cycle.
        while(start < end){
            while(start < end && a[start] <= base)
                //Start traversing from the left. If it is smaller than the benchmark value, continue to walk to the right
                start++;
            //above while At the end of the cycle, the current a[start]The value of is larger than the reference value and should be exchanged with the reference value
            if(start < end){
                //exchange
                int temp = a[start];
                a[start] = a[end];
                a[end] = temp;
                //After the exchange, the exchanged value is also adjusted to the correct position at the same time(Right of reference value)，Therefore, the right side should also move forward one bit at the same time
                end--;
            }    
            while(start < end && a[end] >= base)
                //Start traversing from the right. If it is larger than the benchmark value, continue to walk to the left
                end--;
            //above while At the end of the cycle, the current a[end]The value of is smaller than the reference value and should be exchanged with the reference value
            if(start < end){
                //exchange
                int temp = a[start];
                a[start] = a[end];
                a[end] = temp;
                //After the exchange, the exchanged value is also adjusted to the correct position at the same time(Left of reference value)，Therefore, the left side should also move one bit backward at the same time
                start++;
            }    
            
        }
        //Return here start perhaps end Yes, at this time start and end Is the position of the reference value
        return end;
    }
 
    /**
     * sort
     * @param a
     * @param start
     * @param end
     */
    public static void sort(int[] a, int start, int end){
        if(start > end){ //start >= end ?
            //If there is only one element, there is no need to row down
            return;
        } 
        else{
            //If there is more than one element, continue to divide and sort recursively on both sides
            int partition = divide(a, start, end);
            sort(a, start, partition-1);
            sort(a, partition+1, end);
        }
            
    }


    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a = new int[]{2,7,4,5,10,1,9,3,8,6};
        int[] b = new int[]{1,2,3,4,5,6,7,8,9,10};
        int[] c = new int[]{10,9,8,7,6,5,4,3,2,1};
        int[] d = new int[]{1,10,2,9,3,2,4,7,5,6};
        int[] e = {3};
            
        sort(b, 0, b.length-1);
            
        System.out.println("Sorted results:");
        for(int x : b){
            System.out.print(x+" ");
        }

    }

}

4, Merge sort

public class Sort {
    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = mergeSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    //Merge sort
    public static int[] mergeSort(int[] arr) {
        return mergeSort(arr, 0, arr.length - 1, new int[arr.length]);
    }

    /**
     * Merge sort decomposes the array into only two elements recursively, and puts them into a temporary array according to their size until they are all merged
     *
     * @param arr   Array to be sorted
     * @param left  Left index
     * @param right Right index
     * @param temp  A temporary array that stores the elements after each merge
     * @return
     */
    public static int[] mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) >> 1;
            //Left decomposition
            mergeSort(arr, left, mid, temp);
            //Right decomposition
            mergeSort(arr, mid + 1, right, temp);
            //merge
            merge(arr, left, mid, right, temp);
        }
        return arr;
    }

    //merge
    public static int[] merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left, j = mid + 1, k = 0;
        //Put into temporary array by size
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                temp[k] = arr[i];
                k++;
                i++;
            } else {
                temp[k] = arr[j];
                k++;
                j++;
            }
        }

        //Put the remaining elements into temp Remaining position
        while (i <= mid) {
            temp[k] = arr[i];
            k++;
            i++;
        }
        while (j <= right) {
            temp[k] = arr[j];
            k++;
            j++;
        }

        //Put in order temp The array element is assigned to the original array
        k = 0;
        int l = left;
        while (l <= right) {
            arr[l] = temp[k];
            k++;
            l++;
        }

        return arr;
    }

}

5, Cardinality sort

public class RadixSort {

    public static void main(String[] args) {
        int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56};
        int[] sortResult = radixSort(arr);
        System.out.println(Arrays.toString(sortResult));
    }

    /**
     * Cardinality sorting:
     * According to the bits, tens and hundreds of each number The value of (0 ~ 9) is put into the bucket (the rule and count sorting are the same), so 10 buckets are required
     *
     * @param arr
     * @return
     */
    public static int[] radixSort(int[] arr) {
        //Create and initialize 10 buckets
        ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(10);
        for (int i = 0; i < 10; i++) {
            bucketList.add(new LinkedList<>());
        }

        //Find the maximum value in the data
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (max < arr[i]) {
                max = arr[i];
            }
        }

        //Gets the number of digits of the maximum value
        int maxRadix = (max + "").length();
        //Start with a bit
        for (int i = 0; i < maxRadix; i++) {
            //Put the elements to be sorted into the bucket
            for (int j = 0; j < arr.length; j++) {
                //Gets the value on the corresponding bit of the number
                int radix = arr[j] / (int) Math.pow(10, i) % 10;
                //Put it into the corresponding bucket
                bucketList.get(radix).add(arr[j]);
            }
            //Put the elements in the bucket back into the original array
            int k = 0;
            for (int j = 0; j < 10; j++) {
                for (Integer number : bucketList.get(j)) {
                    arr[k++] = number;
                }
                bucketList.get(j).clear();
            }
        }
        return arr;
    }
}

Another: the stability of sorting algorithm

1. Definition of stability
Assuming that there are multiple records with the same keyword in the record sequence to be sorted, if they are sorted, the relative order of these records remains unchanged, that is, in the original sequence, ri=rj, and ri is before rj, while in the sorted sequence, ri is still before rj, then this sort of sorting algorithm is said to be stable; Otherwise, it is called unstable.

Take chestnuts for example: take {6,2,4,6,1}

a[0]	a[1]	a[2]	a[3]	a[4]
6	2	4	6	1

There are two [0, a] and [3]. There are two possibilities for sorting results:

1	2	4	6	6
Original a[4]	Original a[1]	Original a[2]	Original a[0]	Original a[3]
Original a[4]	Original a[1]	Original a[2]	Original a[3]	Original a[0]

If after sorting, a[0] can be guaranteed to be ahead of a[3], that is, their original order remains unchanged, then this sorting algorithm is stable. On the contrary, if the original order cannot be guaranteed, this algorithm is unstable.

2. Stability of common algorithms
Heap sort, quick sort, Hill sort and direct selection sort are not stable sorting algorithms, while cardinal sort, bubble sort, direct insertion sort, half insertion sort and merge sort are stable sorting algorithms.

3. Significance of stability
1. If you simply sort numbers, then stability will be meaningless.
2. If the sorting content is only a digital attribute of a complex object, the stability will still be meaningless (the cost of the so-called exchange operation has been included in the cost of the algorithm. If you dislike this cost, you might as well change the algorithm?)
3. If the content to be sorted is multiple numeric attributes of a complex object, but its original initial order is meaningless, then the stability will still be meaningless.
4. Unless the content to be sorted is multiple digital attributes of a complex object, and its original initial order has meaning, we need to maintain the meaning of the original sorting on the basis of secondary sorting, so we need to use a stable algorithm. For example, the content to be sorted is a group of objects that were originally sorted according to the price. Now they need to be sorted according to the sales volume. Using the stability algorithm, the objects that want the same sales volume can still maintain the sorting display of the price. Only those with different sales volume will be reordered. (of course, if the requirements do not need to maintain the initial sorting significance, it will still be meaningless to use the stability algorithm).

reference resources:

https://www.cnblogs.com/songjilong/p/12234856.html

https://blog.csdn.net/sunxianghuang/article/details/51872360

https://blog.csdn.net/it_zjyang/article/details/53406764

https://www.cnblogs.com/hydor/p/3530593.html

https://blog.csdn.net/chenliguan/article/details/53037482