1, Title Requirements

• The n queen problem studies how to place n queens in n × N's chessboard, and the Queens can't attack each other.
• Give you an integer n and return the solution of all different queen n problems.
• Each solution contains a different chess placement scheme for the n-queen problem, in which 'Q' and ' They represent the queen and the vacant seat respectively.
• Example 1:

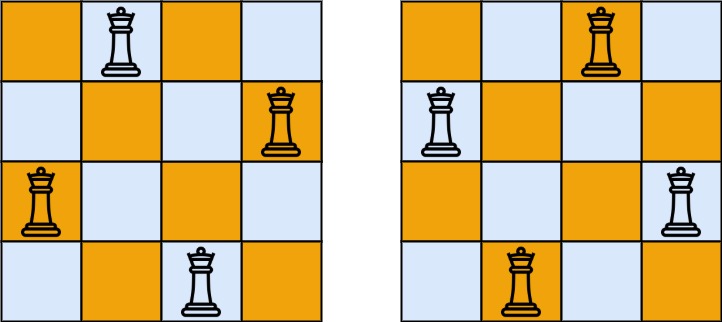
Input: n = 4
 Output:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: as shown in the figure above, there are two different solutions to the 4 queen problem.

• Example 2:

Input: n = 1
 Output:[["Q"]]

• Tip: 1 < = n < = 9.

2, Solution idea

• "N queens problem" studies how to place n queens in n × N's chessboard, and the Queens can't attack each other. The Queen's walking method is: she can walk horizontally and diagonally, and the number of squares is unlimited. Therefore, requiring queens not to attack each other is equivalent to requiring any two queens not to be on the same row, column and slash.
• The intuitive approach is to place n queens in n × All possible situations on the chessboard of N, and judge whether the queen does not attack each other for each situation. The time complexity of violence enumeration is very high, so it must be optimized by using constraints.
• Obviously, each queen must be in different rows and columns, so put n queens in n × On the chessboard of N, there must be only one queen in each row and only one queen in each column, and any two queens cannot be on the same slash. Based on the above findings, possible solutions can be found by backtracking.
• The specific method of backtracking is to use an array to record the column subscript of the queen placed in each row, and place a queen in each row in turn. Every time a newly placed queen cannot attack an already placed Queen: that is, the newly placed queen cannot be in the same column and on the same slash as any already placed queen, and update the queen column subscript of the current row in the array. When all N queens are placed, a possible solution is found. When a possible solution is found, the array is converted into a list representing the state of the chessboard, and the list of the state of the chessboard is added to the return list.
• Since each queen must be in a different column, no other queen can be placed in the column where the queen has been placed. The first queen has N columns to choose from, the second queen has at most N − 1 columns to choose from, and the third queen has at most N − 2 columns to choose from (if you consider that you can't be on the same slash, there are fewer possible choices), so all possible situations will not exceed N! The time complexity of traversing these cases is O(N!).
• In order to reduce the total time complexity, it is necessary to quickly judge whether a queen can be placed in each position every time when placing a queen. Obviously, the best situation is to judge whether there is a queen in the column where the position is located and on the two slashes within the time of O(1).

3, Solving algorithm

① Set based backtracking

• In order to judge whether there is a queen on the column where a position is located and on the two slashes, three sets of columns, diagonals1 and diagonals2 are used to record whether there is a queen on each column and each slash in both directions.
• The representation of columns is very intuitive. There are N columns in total. The subscript of each column ranges from 0 to N − 1. Each column can be clearly represented by using the subscript of the column.
• How to represent slashes in two directions? For slashes in each direction, you need to find the relationship between row and column subscripts at each position on the slash.
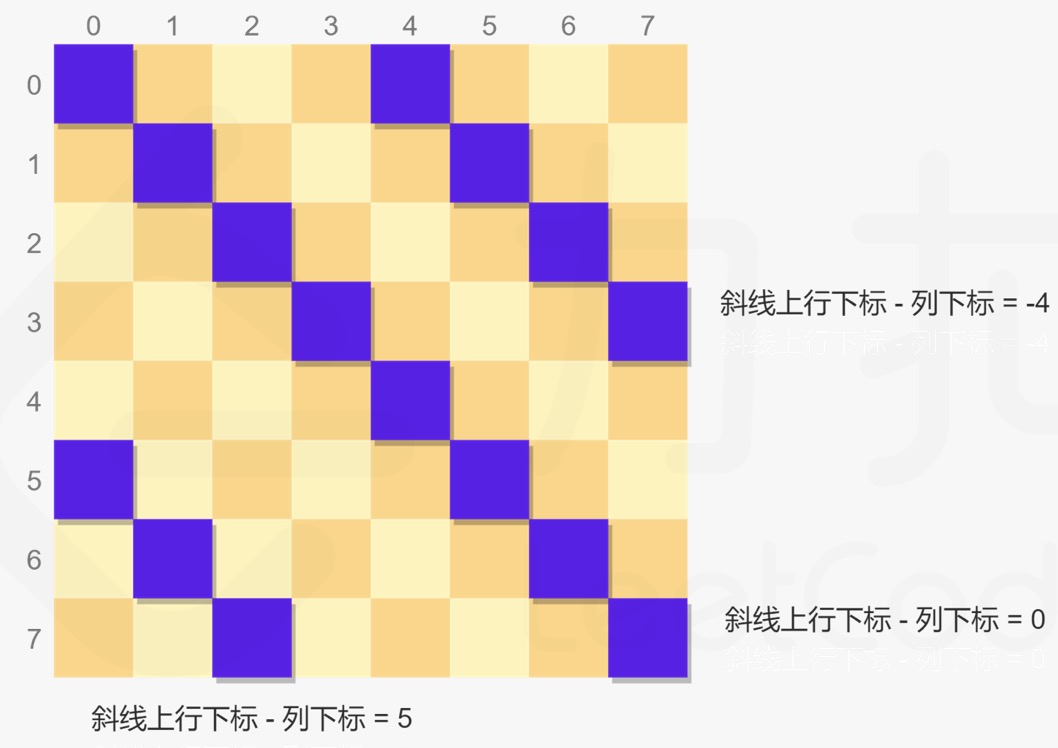
• The slash in direction 1 is from top left to bottom right. Each position on the same slash satisfies that the difference between row subscript and column subscript is equal, for example, (0,0) and (3,3) are on the slash in the same direction. Therefore, using the difference between row subscript and column subscript can clearly indicate the slash in each direction.

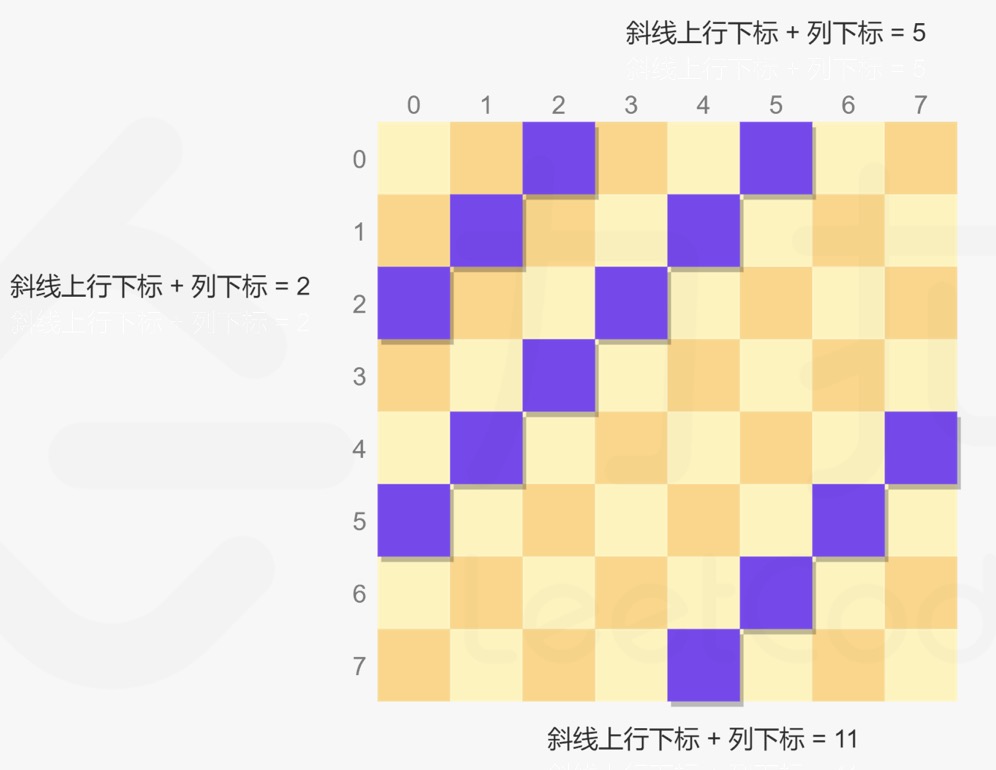
• The slash in direction 2 is from top right to bottom left. Each position on the same slash satisfies that the sum of row subscript and column subscript is equal, for example, (3,0) and (1,2) are on the slash in direction 2. Therefore, using the sum of row subscripts and column subscripts can clearly represent the slash in each direction.

• Each time the queen is placed, judge whether each position is in three sets. If none of the three sets contains the current position, the current position is the position where the queen can be placed.
• Java example:

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> solutions = new ArrayList<List<String>>();
        int[] queens = new int[n];
        Arrays.fill(queens, -1);
        Set<Integer> columns = new HashSet<Integer>();
        Set<Integer> diagonals1 = new HashSet<Integer>();
        Set<Integer> diagonals2 = new HashSet<Integer>();
        backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
        return solutions;
    }

    public void backtrack(List<List<String>> solutions, int[] queens, int n, int row, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {
        if (row == n) {
            List<String> board = generateBoard(queens, n);
            solutions.add(board);
        } else {
            for (int i = 0; i < n; i++) {
                if (columns.contains(i)) {
                    continue;
                }
                int diagonal1 = row - i;
                if (diagonals1.contains(diagonal1)) {
                    continue;
                }
                int diagonal2 = row + i;
                if (diagonals2.contains(diagonal2)) {
                    continue;
                }
                queens[row] = i;
                columns.add(i);
                diagonals1.add(diagonal1);
                diagonals2.add(diagonal2);
                backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
                queens[row] = -1;
                columns.remove(i);
                diagonals1.remove(diagonal1);
                diagonals2.remove(diagonal2);
            }
        }
    }

    public List<String> generateBoard(int[] queens, int n) {
        List<String> board = new ArrayList<String>();
        for (int i = 0; i < n; i++) {
            char[] row = new char[n];
            Arrays.fill(row, '.');
            row[queens[i]] = 'Q';
            board.add(new String(row));
        }
        return board;
    }
}

• C + + example:

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        auto solutions = vector<vector<string>>();
        auto queens = vector<int>(n, -1);
        auto columns = unordered_set<int>();
        auto diagonals1 = unordered_set<int>();
        auto diagonals2 = unordered_set<int>();
        backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
        return solutions;
    }

    void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
        if (row == n) {
            vector<string> board = generateBoard(queens, n);
            solutions.push_back(board);
        } else {
            for (int i = 0; i < n; i++) {
                if (columns.find(i) != columns.end()) {
                    continue;
                }
                int diagonal1 = row - i;
                if (diagonals1.find(diagonal1) != diagonals1.end()) {
                    continue;
                }
                int diagonal2 = row + i;
                if (diagonals2.find(diagonal2) != diagonals2.end()) {
                    continue;
                }
                queens[row] = i;
                columns.insert(i);
                diagonals1.insert(diagonal1);
                diagonals2.insert(diagonal2);
                backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
                queens[row] = -1;
                columns.erase(i);
                diagonals1.erase(diagonal1);
                diagonals2.erase(diagonal2);
            }
        }
    }

    vector<string> generateBoard(vector<int> &queens, int n) {
        auto board = vector<string>();
        for (int i = 0; i < n; i++) {
            string row = string(n, '.');
            row[queens[i]] = 'Q';
            board.push_back(row);
        }
        return board;
    }
};

② Backtracking based on bit operation

• Method ① use three set records to record whether there is a queen on each column and each slash in two directions respectively. Each set contains at most N elements, so the spatial complexity of the set is O(N). If the Queen's information is recorded by bit operation, the spatial complexity of recording Queen's information can be reduced from O(N) to O(1).
• Specifically, use three integers columns, diagonals1 and diagonals2 to record whether there is a queen on each column and each slash in both directions, and each integer has N binary bits. Each column of the chessboard corresponds to a digit in the binary representation of each integer. The leftmost column of the chessboard corresponds to the lowest binary bit of each integer, and the rightmost column corresponds to the highest binary bit of each integer.
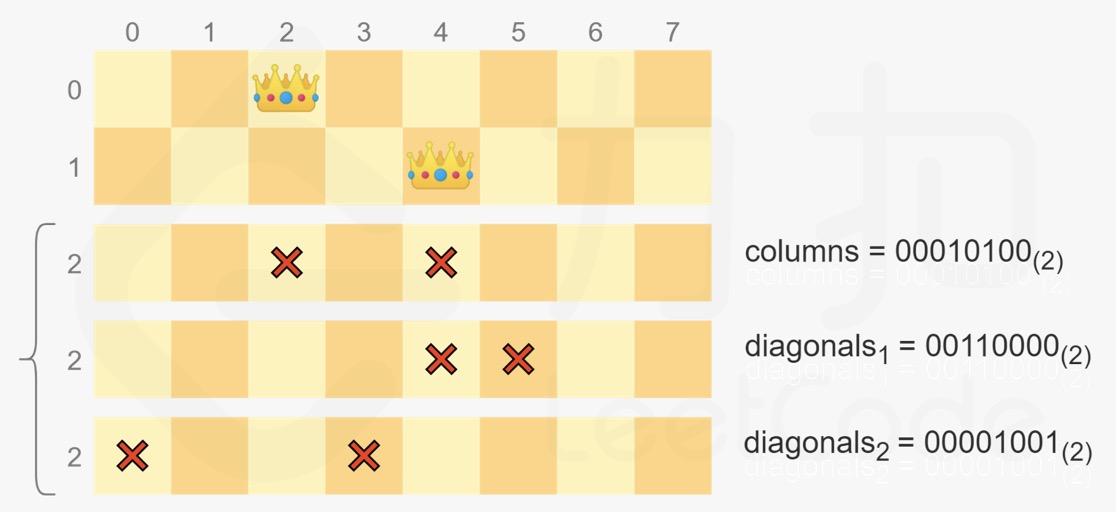
• So how to update the value of three integers according to the queen placed each time? Before talking about the specific calculation method, let's first say an example: the side length of the chessboard and the number of queens N=8. If the first two rows of the chessboard place queens in column 2 and column 4 respectively (the subscript starts from 0), the first two rows of the chessboard are shown in the figure below:

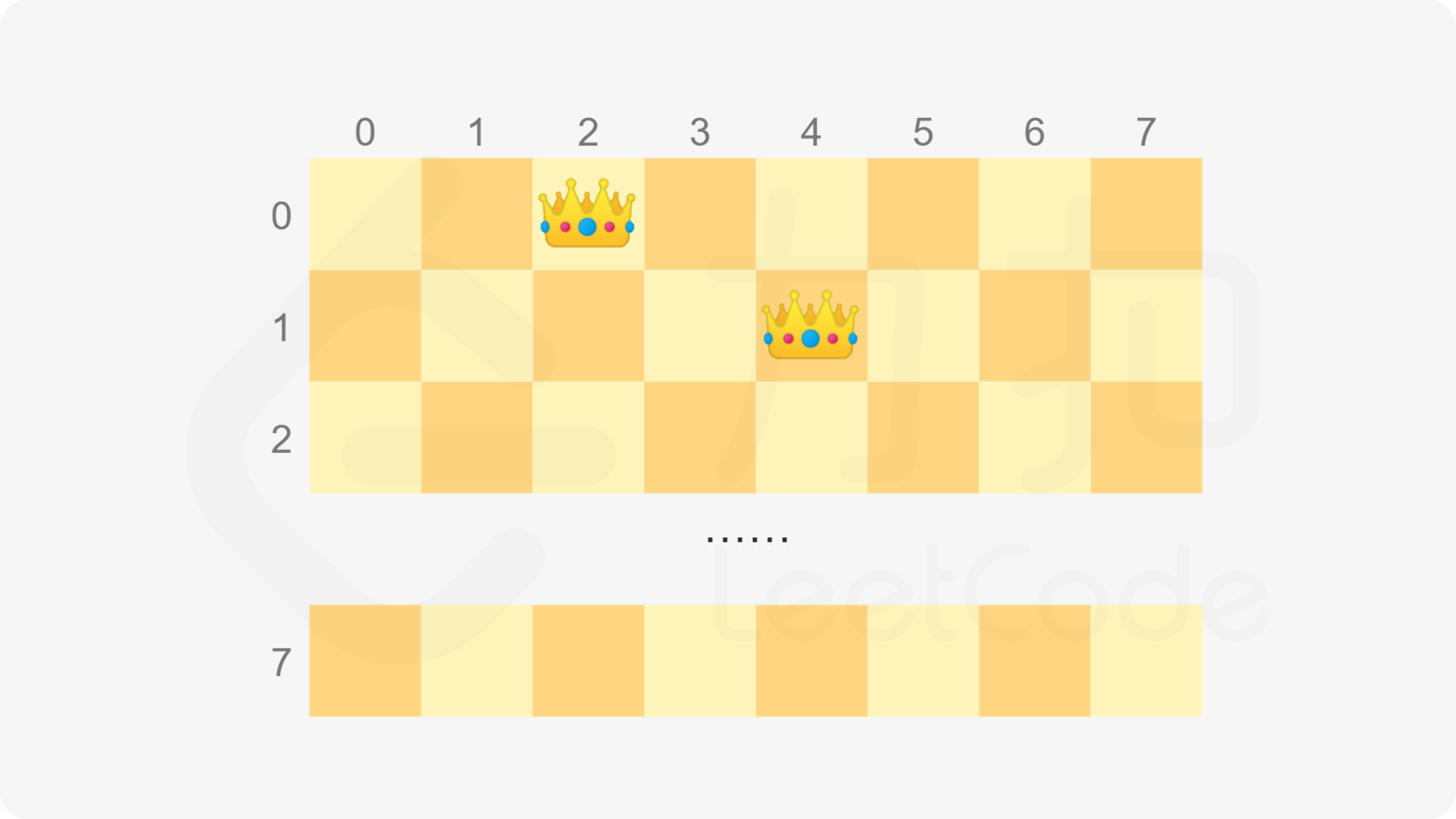
• If you want to place the queen on the next line, where can't you place it? Use 0 to represent the position where the queen can be placed, and 1 to represent the position where the queen cannot be placed.
• The newly placed queen cannot be placed in the same column as any queen already placed, so it cannot be placed in columns 2 and 4, corresponding to columns=00010100(2).
• The newly placed queen cannot be placed on the slash in the same direction (from top left to bottom right) as any placed queen, so it cannot be placed in columns 4 and 5, corresponding to diagonals1 = 00110000(2). Among them, column 4 is the position where the queen in column 2 of the first two rows moves two steps to the right, and column 5 is the position where the queen in column 4 of the previous row moves one step to the right.
• The newly placed queen cannot be placed on the slash in the same direction 2 (from top right to bottom left) as any placed queen, so it cannot be placed in columns 0 and 3, corresponding to diagonals2 = 00110000(2). Among them, column 0 is the position where the queen in column 2 of the first two rows moves two steps to the left, and column 3 is the position where the queen in column 4 of the previous row moves one step to the left.

• Thus, the calculation method of three integers can be obtained:
• • Initially, the values of the three integers are equal to 0, indicating that no queen is placed;
• • Place the queen in the current row. If the queen is placed in column I, set the value of the i-th binary bit of the three integers (i-th binary bit from low to high) to 1;
• • When entering the next row, the value of columns remains unchanged. Diagonals1 moves left by one bit and diagonals2 moves right by one bit. Because the leftmost column of the chessboard corresponds to the lowest binary bit of each integer, that is, the rightmost binary bit of each integer, Therefore, the shift operation direction of the integer is opposite to that of the chessboard (the shift operation direction of the chessboard is to shift diagonals1 right by one bit and diagonals2 left by one bit).
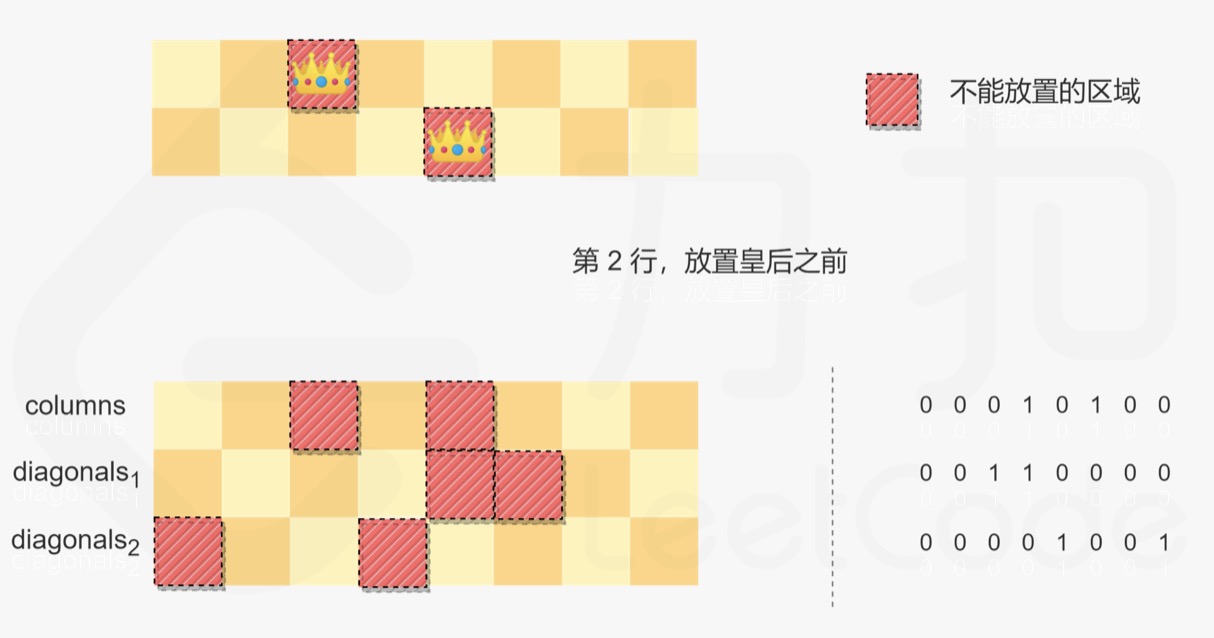
• Position of lines 0 and 1:

• Line 2 before placing the Queen:

• Operate the above three numbers by bit or to get the area where the second line cannot be placed:
  
• The queen in Row 2 can be placed in columns 1, 6 and 7, and placed in column 6. The sixth binary position of three integers is 1:
  
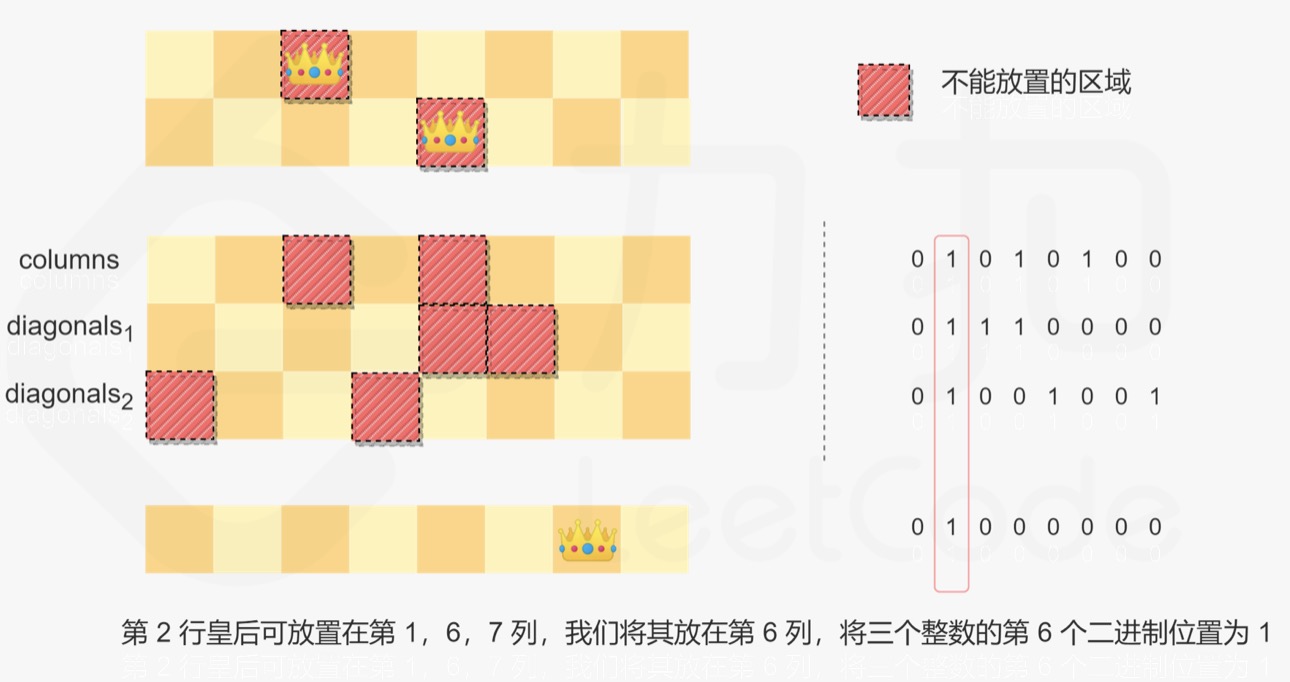
• Lines 0, 1 and 2 are placed:
  

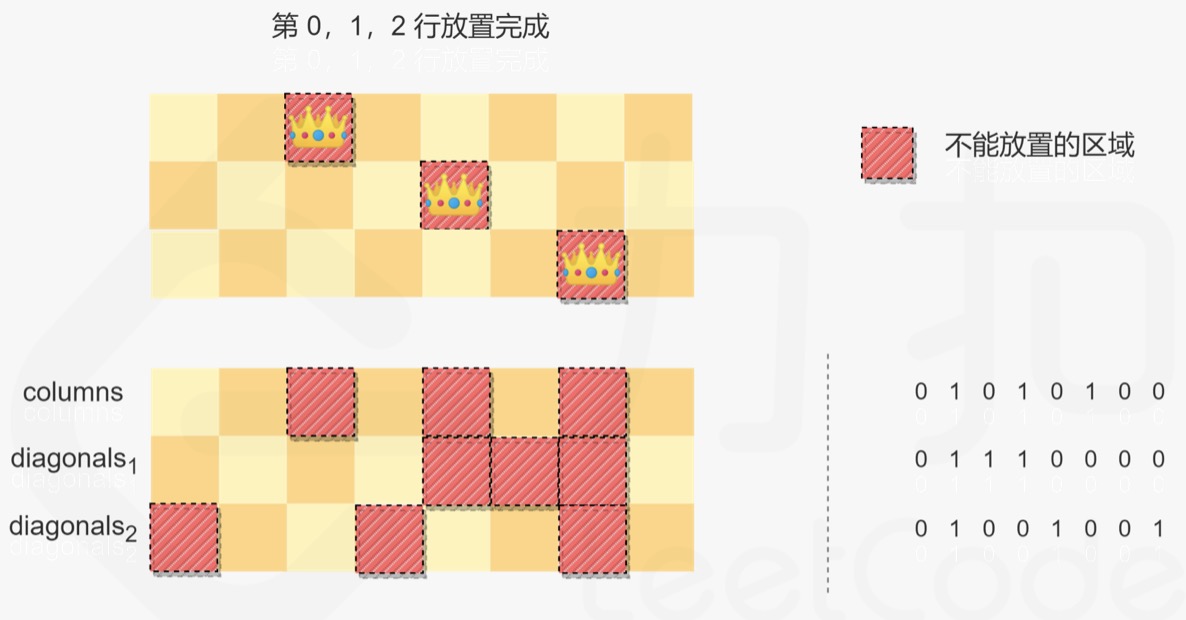
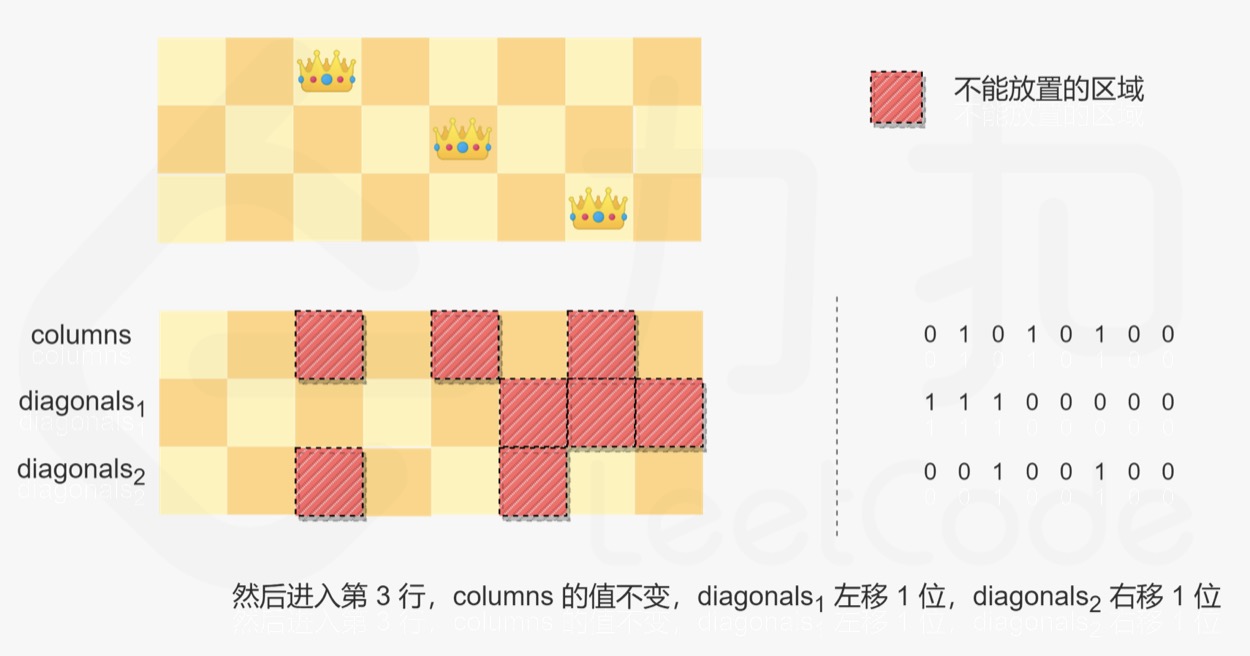
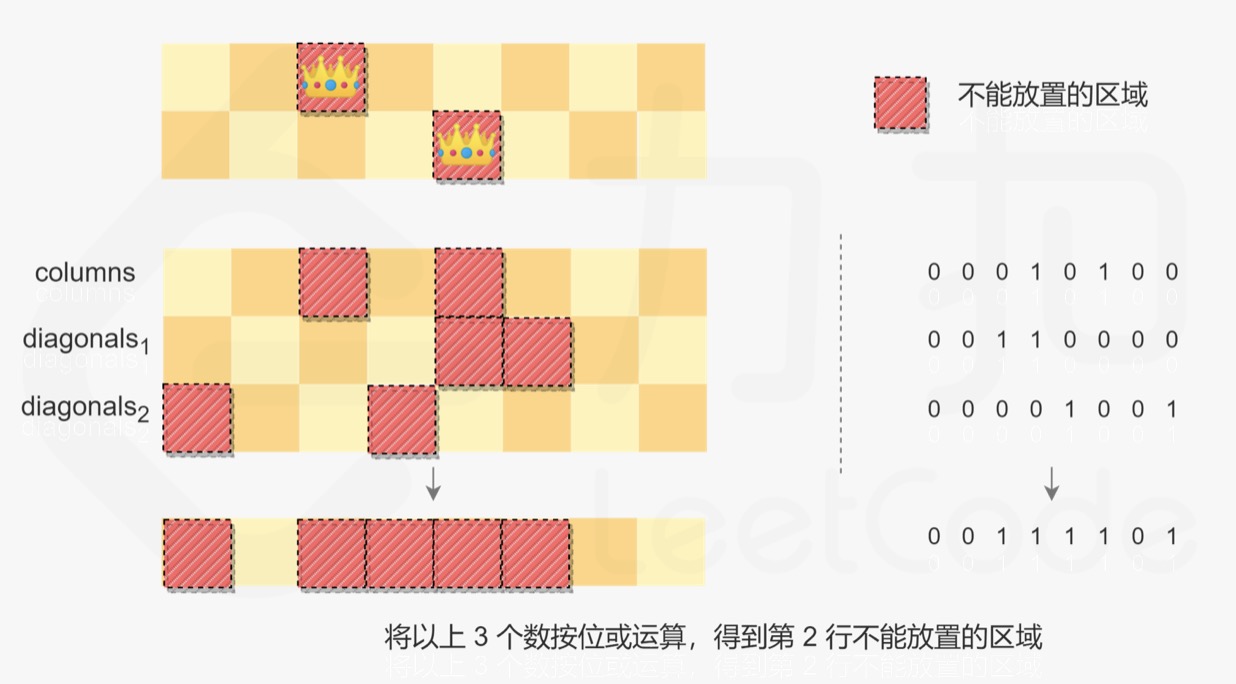
• Each time the queen is placed, the result of the bitwise OR operation of the three integers is the position where the queen cannot be placed, and the other positions are the positions where the queen can be placed. You can get the positions where Queens can be placed by (2n − 1) & (∼ (columns ∣ diagonals1 ∣ diagonals2)) (the position with a value of 1 indicates the position where Queens can be placed), and then traverse these positions to try to place queens and obtain possible solutions.
• When traversing the position where the queen can be placed, the following two properties of bitwise and operation can be used:
• • X & (− x) can obtain the position of the lowest 1 in the binary representation of X;
• • X & (x − 1) the lowest 1 in the binary representation of X can be set to 0.
• The specific method is to obtain the lowest position in the position where the queen can be placed each time, set the value of this bit to 0, and try to place the queen in this position. In this way, you can traverse each position where you can place the queen.
• Java example:

class Solution {
    public List<List<String>> solveNQueens(int n) {
        int[] queens = new int[n];
        Arrays.fill(queens, -1);
        List<List<String>> solutions = new ArrayList<List<String>>();
        solve(solutions, queens, n, 0, 0, 0, 0);
        return solutions;
    }

    public void solve(List<List<String>> solutions, int[] queens, int n, int row, int columns, int diagonals1, int diagonals2) {
        if (row == n) {
            List<String> board = generateBoard(queens, n);
            solutions.add(board);
        } else {
            int availablePositions = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2));
            while (availablePositions != 0) {
                int position = availablePositions & (-availablePositions);
                availablePositions = availablePositions & (availablePositions - 1);
                int column = Integer.bitCount(position - 1);
                queens[row] = column;
                solve(solutions, queens, n, row + 1, columns | position, (diagonals1 | position) << 1, (diagonals2 | position) >> 1);
                queens[row] = -1;
            }
        }
    }

    public List<String> generateBoard(int[] queens, int n) {
        List<String> board = new ArrayList<String>();
        for (int i = 0; i < n; i++) {
            char[] row = new char[n];
            Arrays.fill(row, '.');
            row[queens[i]] = 'Q';
            board.add(new String(row));
        }
        return board;
    }
}

• C + + example:

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        auto solutions = vector<vector<string>>();
        auto queens = vector<int>(n, -1);
        solve(solutions, queens, n, 0, 0, 0, 0);
        return solutions;
    }

    void solve(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, int columns, int diagonals1, int diagonals2) {
        if (row == n) {
            auto board = generateBoard(queens, n);
            solutions.push_back(board);
        } else {
            int availablePositions = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2));
            while (availablePositions != 0) {
                int position = availablePositions & (-availablePositions);
                availablePositions = availablePositions & (availablePositions - 1);
                int column = __builtin_ctz(position);
                queens[row] = column;
                solve(solutions, queens, n, row + 1, columns | position, (diagonals1 | position) >> 1, (diagonals2 | position) << 1);
                queens[row] = -1;
            }
        }
    }

    vector<string> generateBoard(vector<int> &queens, int n) {
        auto board = vector<string>();
        for (int i = 0; i < n; i++) {
            string row = string(n, '.');
            row[queens[i]] = 'Q';
            board.push_back(row);
        }
        return board;
    }
};