Support Vector Machine
Pre knowledge: Lagrange number multiplication, dual problem, kernel technique
Lagrange number multiplication
For constrained optimization problems:
Example:
Known x>0,y>0,x+2y+2xy=8,be x+2y Minimum value of__.
Solution:
Introduction parameters λ \lambda λ Construct new function L: x + 2 y + λ ( x + 2 y + 2 x y − 8 ) x+2y+\lambda(x+2y+2xy-8) x+2y+λ(x+2y+2xy−8)
For x,y,
λ
\lambda
λ Partial derivation:
L
x
=
1
+
λ
(
1
+
2
y
)
=
0
L
y
=
2
+
λ
(
2
+
2
x
)
=
0
L
λ
=
x
+
2
y
+
2
x
y
−
8
=
0
L_x = 1+\lambda(1+2y)=0\\ L_y = 2+\lambda(2+2x)=0\\ \ \ \ \ \ \ L_\lambda = x+2y+2xy-8=0\\
Lx=1+λ(1+2y)=0Ly=2+λ(2+2x)=0 Lλ=x+2y+2xy−8=0
Three equations and three unknowns, x = 2 and y = 1 can be obtained.
That is, when x = 2 and y = 1, the minimum value of x+2y is 4.
Dual problem
Conversion for optimization problems
For example: maxmin - > minmax
The default constrained optimization problem is a weak dual relationship. When the KNN condition is satisfied, it has a strong dual relationship, that is, they are equivalent.
Nuclear technique
For the expansion of high-dimensional features, when the number of samples or hyperplane dimension is too large, the kernel technique can be used to optimize and transform the problem into a finite dimensional problem.
Machine Learning action
This chapter studies the most popular implementation of support vector machines - sequential minimum optimization algorithm.
Advantages: low generalization error rate, low computational overhead and easy to understand results Disadvantages: it is sensitive to parameter adjustment and function selection. The original classifier is only suitable for binary classification without modification. Applicable data types: numerical and nominal data
Principle part
Split hyperplane set is the plane that divides different types of data points. Support vector machine is a classifier composed of these split hyperplanes.
**Support vector refers to those points closest to the separating hyperplane. Maximizing the interval of support vector is the optimization goal of constructing support vector machine
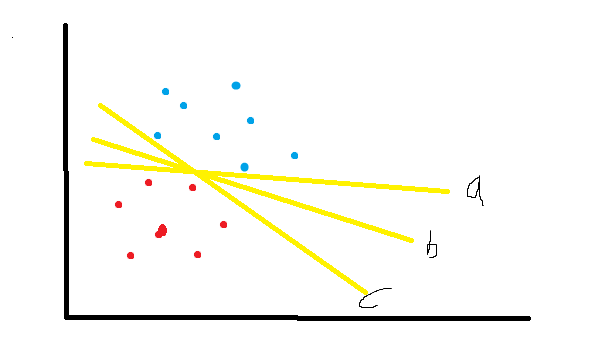
In the figure, a, b and C can all be considered as a segmentation hyperplane. Obviously, the robustness, i.e. generalization ability, of hyperplane b is better than that of a and C.
How to establish a mathematical model to find a high-quality hypersegmentation plane?
Then we need to define an optimization goal, that is, to maximize the spacing of those closest to the hyperdivided surface.
a
r
g
m
a
x
w
,
b
{
m
i
n
(
w
T
∗
x
+
b
)
}
arg\ max_{w,b}\ \{ min(w^T*x+b) \}
arg maxw,b {min(wT∗x+b)}
Among them, W and B are the parameters to be optimized. If it is very difficult to directly solve the model, a series of model transformations are started. Those interested can further study in combination with the video at the beginning of the article and the watermelon book. Here we only comb the process.
- Lagrange equations are obtained by Lagrange multiplier method
- The Lagrange function is transformed into a r g m i n m a x arg\ min max arg minmax problem
- Using the strong duality condition (KKT condition) of duality problem a r g m i n m a x arg\ minmax arg minmax is converted to a r g m a x m i n arg\ maxmin arg maxmin problem
- Because the sample space is not necessarily linearly separable, the relaxation variable is added
At the same time, the parameter of the problem becomes α \alpha α The next step is to solve the problem
The method used in machine learning practice is SMO algorithm.
SMO algorithm pseudo code:
Create a alpha Vector and initialize it to a 0 vector When the number of iterations is less than the maximum number of iterations(External circulation): For each data vector in the dataset(Internal circulation): If the data vector can be optimized: Randomly select another data vector Optimize both vectors at the same time If neither vector can be optimized, exit the inner loop If all vectors are not optimized, increase the number of iterations and continue the next cycle
In fact, SMO algorithm is a more effective greedy algorithm.
code
'''
Created on Nov 4, 2010
Chapter 5 source file for Machine Learing in Action
@author: Peter
'''
from numpy import *
from time import sleep
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
def selectJrand(i, m):
j = i # we want to select any J not equal to i
while (j == i):
j = int(random.uniform(0, m))
return j
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose()
b = 0
m, n = shape(dataMatrix)
alphas = mat(zeros((m, 1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
Ei = fXi - float(labelMat[i]) # if checks if an example violates KKT conditions
if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i, m)
fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
print("L==H")
continue
eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[
j,
:] * dataMatrix[
j, :].T
if eta >= 0 :
print("eta>=0")
continue
alphas[j] -= labelMat[j] * (Ei - Ej) / eta
alphas[j] = clipAlpha(alphas[j], H, L)
if (abs(alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
continue
alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j]) # update i by the same amount as j
# the update is in the oppostie direction
b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[
j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[
j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2) / 2.0
alphaPairsChanged += 1
print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
print("iteration number: %d" % iter)
return b, alphas
def kernelTrans(X, A, kTup): # calc the kernel or transform data to a higher dimensional space
m, n = shape(X)
K = mat(zeros((m, 1)))
if kTup[0] == 'lin':
K = X * A.T # linear kernel
elif kTup[0] == 'rbf':
for j in range(m):
deltaRow = X[j, :] - A
K[j] = deltaRow * deltaRow.T
K = exp(K / (-1 * kTup[1] ** 2)) # divide in NumPy is element-wise not matrix like Matlab
else:
raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m, 1)))
self.b = 0
self.eCache = mat(zeros((self.m, 2))) # first column is valid flag
self.K = mat(zeros((self.m, self.m)))
for i in range(self.m):
self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)
def calcEk(oS, k):
fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei): # this is the second choice -heurstic, and calcs Ej
maxK = -1
maxDeltaE = 0
Ej = 0
oS.eCache[i] = [1, Ei] # set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: # loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue # don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else: # in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k): # after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek]
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
(oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
j, Ej = selectJ(i, oS, Ei) # this has been changed from selectJrand
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j] # changed for kernel
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
updateEk(oS, j) # added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) # update i by the same amount as j
updateEk(oS, i) # added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.K[i, j]
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.K[j, j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else:
return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)): # full Platt SMO
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)
iter = 0
entireSet = True
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: # go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
else: # go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False # toggle entire set loop
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
return oS.b, oS.alphas
def calcWs(alphas, dataArr, classLabels):
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m, n = shape(X)
w = zeros((n, 1))
for i in range(m):
w += multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
def testRbf(k1=1.3):
dataArr, labelArr = loadDataSet('testSetRBF.txt')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) # C=200 important
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
svInd = nonzero(alphas.A > 0)[0]
sVs = datMat[svInd] # get matrix of only support vectors
labelSV = labelMat[svInd]
print("there are %d Support Vectors" % shape(sVs)[0])
m, n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount) / m))
dataArr, labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
m, n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount) / m))
def img2vector(filename):
returnVect = zeros((1, 1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0, 32 * i + j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName) # load the training set
m = len(trainingFileList)
trainingMat = zeros((m, 1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] # take off .txt
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9:
hwLabels.append(-1)
else:
hwLabels.append(1)
trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=('rbf', 10)):
dataArr, labelArr = loadImages('trainingDigits')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
svInd = nonzero(alphas.A > 0)[0]
sVs = datMat[svInd]
labelSV = labelMat[svInd]
print("there are %d Support Vectors" % shape(sVs)[0])
m, n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount) / m))
dataArr, labelArr = loadImages('testDigits')
errorCount = 0
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
m, n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount) / m))
'''#######********************************
Non-Kernel VErsions below
''' #######********************************
class optStructK:
def __init__(self, dataMatIn, classLabels, C, toler): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m, 1)))
self.b = 0
self.eCache = mat(zeros((self.m, 2))) # first column is valid flag
def calcEkK(oS, k):
fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJK(i, oS, Ei): # this is the second choice -heurstic, and calcs Ej
maxK = -1
maxDeltaE = 0
Ej = 0
oS.eCache[i] = [1, Ei] # set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: # loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue # don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else: # in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEkK(oS, k): # after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek]
def innerLK(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
(oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
j, Ej = selectJ(i, oS, Ei) # this has been changed from selectJrand
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print ("L==H")
return 0
eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
updateEk(oS, j) # added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) # update i by the same amount as j
updateEk(oS, i) # added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (
oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else:
return 0
def smoPK(dataMatIn, classLabels, C, toler, maxIter): # full Platt SMO
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
iter = 0
entireSet = True
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: # go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
else: # go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False # toggle entire set loop
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
return oS.b, oS.alphas
import svm as svmMLiA
import numpy as np
import matplotlib.pyplot as plt
dataArr,labelArr =svmMLiA.loadDataSet('testSet.txt')
# Dataset, category label, constant C, fault tolerance, maximum number of cycles to exit
b,alphas= svmMLiA.smoSimple(dataArr,labelArr,0.6,0.001,40)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# There will be problems with the Chinese display in matplotlib drawing. You need to set the default font in these two lines
plt.xlabel('X')
plt.ylabel('Y')
plt.xlim(xmax=12,xmin=-2.5)
plt.ylim(ymax=10,ymin=-10)
# Draw two (0-9) coordinate axes and set the axis labels x, y
x1=list();x2=list()
y1=list();y2=list()
for j in range(len(labelArr)):
if labelArr[j]==1:
x1.append(dataArr[j][0])
y1.append(dataArr[j][1])
else :
x2.append(dataArr[j][0])
y2.append(dataArr[j][1])
print(x1)
print(y1)
colors1 = '#00CED1'
colors2 = '#DC143C'
area = np.pi*4**2
plt.scatter(x1,y1,s=area,c=colors1,alpha=0.4,label='category A')
plt.scatter(x2,y2,s=area,c=colors2,alpha=0.4,label='category B')
plt.plot()
plt.legend()
plt.savefig('1.png',dpi=300)
plt.show()
epilogue
- SVM is the product of rigorous mathematical proof.
- When the distribution is too single, it is difficult to extract the feature set.