1. Title

Given two integer arrays inorder and postorder, inorder is the middle order traversal of the binary tree and postorder traversal of the same tree, please construct and return this binary tree.

Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output:[3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1]
Output:[-1]

Tips:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder and postorder are made up of different values
• Every value in the postorder is in the inorder
• inorder is guaranteed to be a middle order traversal of the tree
• Postorder is guaranteed to be a postorder traversal of the tree

2. Train of thought

(recursive) O ( n ) O(n) O(n)

Given two integer arrays inorder and postorder, where inorder is the middle order traversal of the binary tree and postorder traversal of the same tree, let's return to the binary tree.

Example:

As shown in the example, inorder = [9,3,15,20,7], postorder = [9,15,7,20,3], we can construct a binary tree as shown in the above figure.

Binary tree:

• The order of traversal in binary tree is: left root right;
• The post order traversal order of binary tree is: left and right roots;

For this problem, we can recursively establish the whole binary tree: first create the root node, then recursively create the left and right subtrees, and point the pointer to the two subtrees.

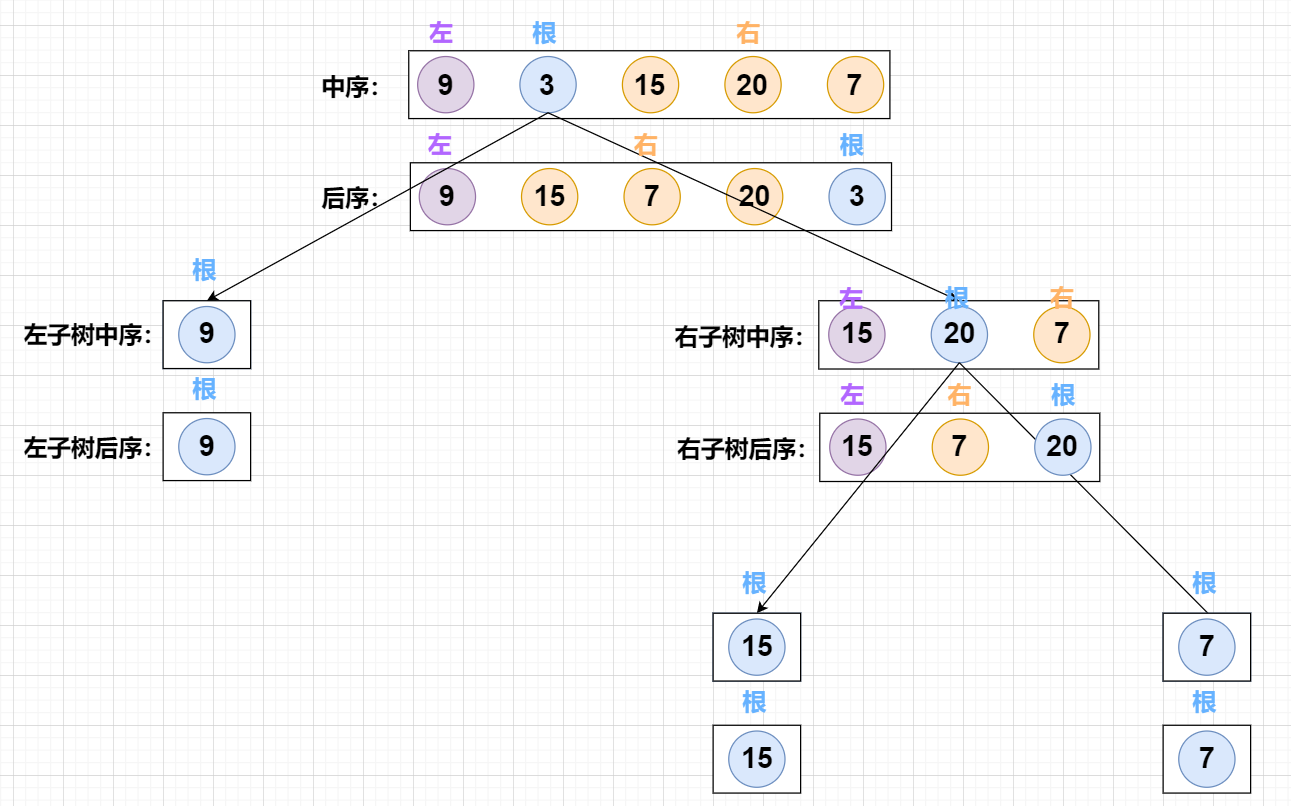
As shown in the figure above, the recursive process is the establishment process of binary tree. After having a general understanding of the establishment process of binary tree, the next step is to determine the boundary of left and right subtrees in middle order and post order arrays.

How to determine the left and right boundaries of subtree?

According to the nature of binary tree, we can take the following steps in turn:

• 1. First use the postorder traversal to find the root node: the last number of postorder traversal is the value of the root node;

• 2. Find the position k of the root node in the middle order traversal, then the left side of k is the middle order traversal of the left subtree, and the right side is the middle order traversal of the right subtree;

• 3. Suppose that IL and IR correspond to the left and right endpoints of the sequence traversal interval in the subtree, and PL and PR correspond to the left and right endpoints of the sequence traversal interval after the subtree. Then the middle order traversal interval of the left subtree is

  [il, k - 1], the middle order traversal interval of the right subtree is [k + 1, ir].

• 4. It can be seen from step 3 that the length of the middle order traversal of the left subtree is k - 1 - il + 1. Since the length of the middle order traversal and the post order traversal of a tree is the same, the length of the post order traversal is also k - 1 - il + 1. In this way, according to the length of post order traversal, we can deduce that the interval of post order traversal of left subtree is [pl, pl + k - 1 - il], and the interval of post order traversal of right subtree is [pl + k - 1 - il + 1, pr - 1].

It may not be easy to understand the above derivation process only by words. We draw a picture to help understand:

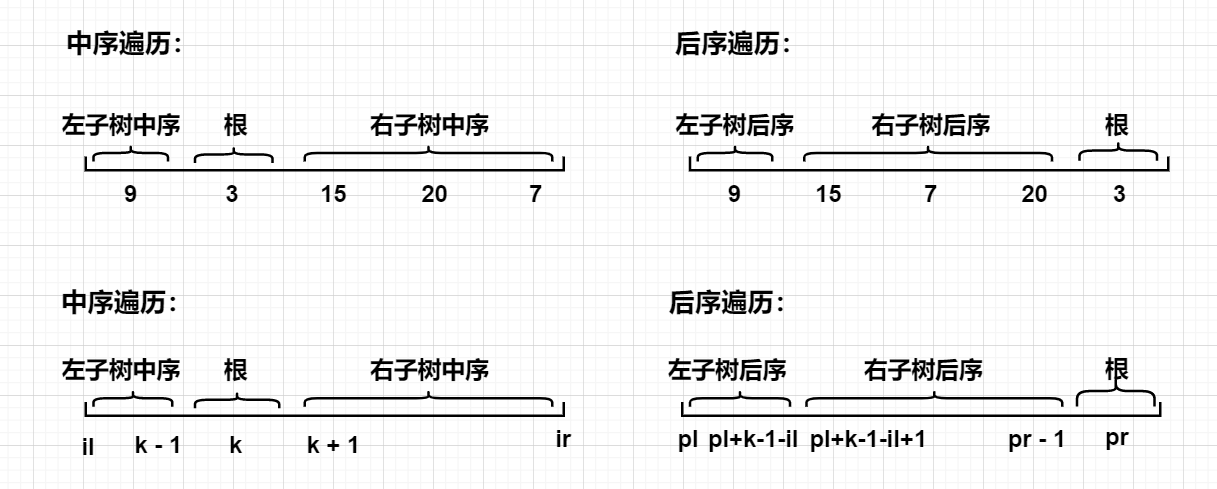
The determination of the boundary of the order and post order traversal in the left and right subtrees is the biggest difficulty of this problem. Understanding this point, more than half of this problem will be completed.

How to quickly locate the root node in the middle order traversal?

A simple method is to directly scan the results of the whole middle order traversal and find the root node, but it has high time complexity. We can consider using a hash table to help us quickly locate the root node. For each key value pair in the hash map, the key represents an element (the value of the node), and the value represents its position in the middle order traversal. In this way, the operation of finding the location of the root node in the middle order traversal only needs O ( 1 ) O(1) O(1).

As shown in the figure:

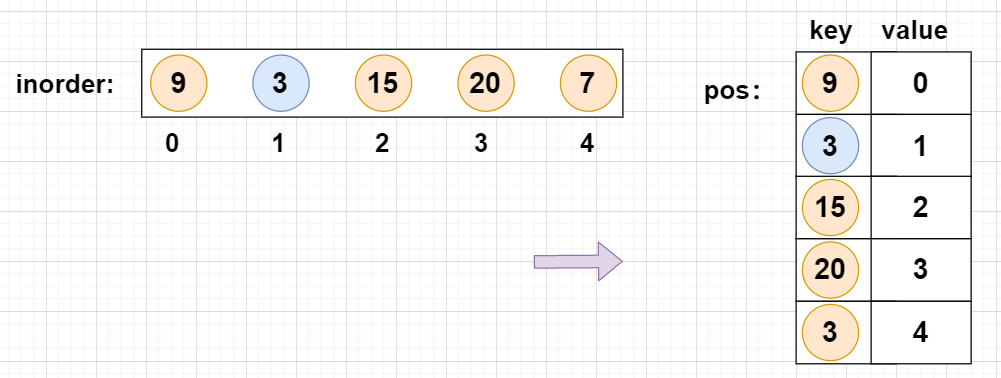
The specific process is as follows:

• 1. Create a hash table pos to record the position of each value in the middle order traversal.
• 2. First use the postorder traversal to find the root node: the last number of postorder traversal is the value of the root node;
• 3. Determine the post order traversal and middle order traversal of the left and right subtrees, create the left and right subtrees recursively, and then create the root node.
• 4. Finally, point the left and right pointers of the root node to two subtrees.

Time complexity analysis: it is necessary to find the location of the root node O ( 1 ) O(1) O(1), the time required to create each node is O ( 1 ) O(1) O(1), so the total time complexity is O ( n ) O(n) O(n).

3. c + + code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        for(int i = 0; i < n; i++){
            pos[inorder[i]] = i;     //Record the position of the root node traversed in sequence
        }
        return dfs(inorder, postorder, 0, n - 1, 0, n - 1);
    }
    TreeNode* dfs(vector<int>& inorder, vector<int>& postorder,int il, int ir, int pl, int pr){
        if(il > ir) return nullptr;
        int k = pos[postorder[pr]];   //Middle order traversal root node position
        TreeNode* root = new TreeNode(postorder[pr]); //Create root node
        root->left = dfs(inorder, postorder, il, k - 1, pl, pl + k - 1 - il);
        root->right = dfs(inorder, postorder, k + 1, ir, pl + k - 1 - il + 1, pr - 1);
        return root;
    }
};

4. Java code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer,Integer> pos = new HashMap<Integer,Integer>();
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int n = inorder.length;
        for(int i = 0; i < n; i++)
            pos.put(inorder[i], i);  //Record the position of the root node traversed in sequence
        return dfs( inorder, postorder, 0, n - 1, 0, n - 1);   
    }
     public TreeNode dfs(int[] inorder, int[] postorder, int il, int ir,int pl, int pr)
    {
        if(pl > pr ) return null;
        int k = pos.get(postorder[pr]);
        TreeNode root = new TreeNode(postorder[pr]);
        root.left  = dfs(inorder, postorder, il, k - 1, pl, pl + k - 1 - il);
        root.right = dfs(inorder, postorder, k + 1, ir, pl + k - 1 - il + 1, pr - 1);
        return root;     
    }
}