Quick sort
graphic
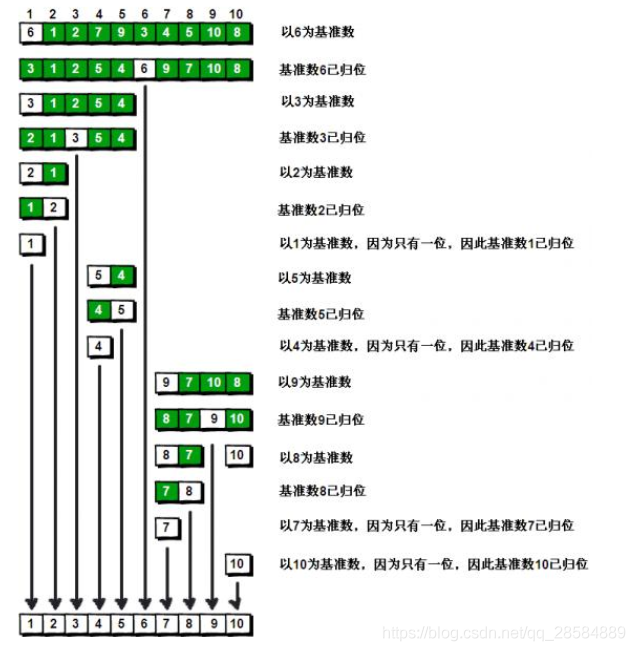
First find the left sentry as the reference number, move the right sentry to a number smaller than the reference number, and then move the left sentry to a number larger than the right sentry.
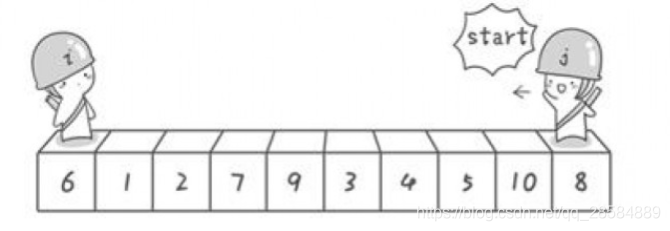
Swap two numbers
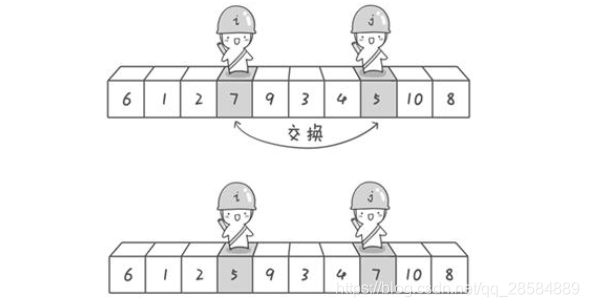
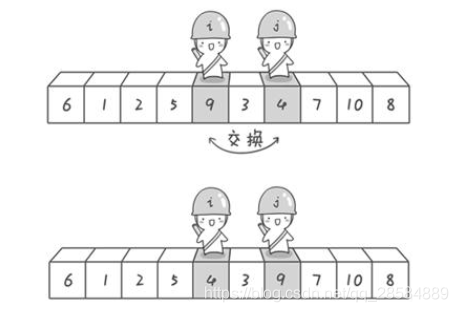
Repeat the process until the two sentinels meet
Exchange the benchmark number with the original number after meeting
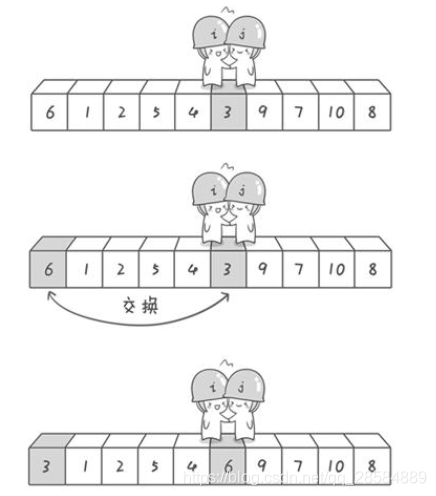
In this way, the first round of exchange is completed. It can be found that the reference number has been returned, and the numbers on the left side of the reference number are smaller than the reference number, and the numbers on the right side are larger than the reference number. Just recurse left and right.
Recursive tree
Template code
void qsort(int l,int r){
if(l>=r) return;
int sol=a[l];
int i=l,j=r;
while(i!=j){
while(a[j]>=sol&&i<j)j--;
while(a[i]<=sol&&i<j) i++;
if(i<j) swap(a[i],a[j]);
}
swap(a[l],a[i]);
qsort(l,i-1);
qsort(i+1,r);
}
example
Just change the template to
void qsort(int l,int r){
int sol=a[l];
int i=l,j=r;
while(i!=j){
while(a[j]>=sol&&i<j)j--;
while(a[i]<=sol&&i<j) i++;
if(i<j) swap(a[i],a[j]);
}
swap(a[l],a[i]);
if(k==i){
p=a[i];
return;
}
else if(k<i) qsort(l,i-1);
else qsort(i+1,r);
}
Because we only need the k-th decimal, which is larger or smaller than k, we don't need to waste time recursing
- The k-th decimal 2
You only need to merge the two groups of inputs
Merge sort
graphic
The first step is to divide the original array in half until there is only one element left.
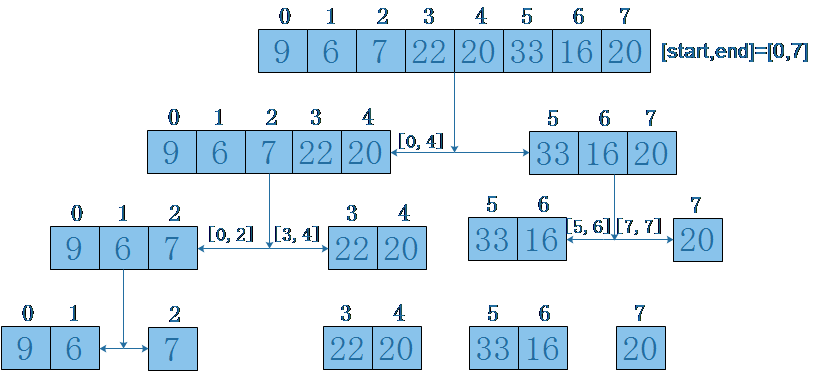
The second step is to merge the separated arrays that have been smaller in turn
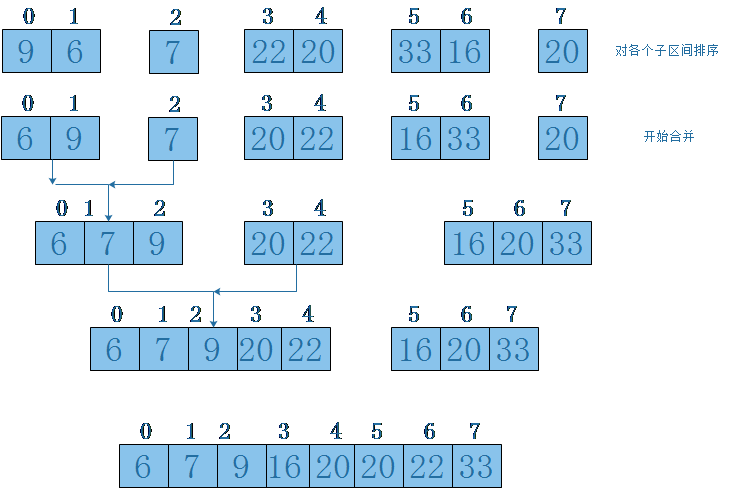
Template code
void merge(int head,int tail){
int mid=(head+tail)/2;
int s=head,e=mid+1,k=0;
while(s<=mid&&e<=tail){
if(a[s]>a[e]) temp[k++]=a[e++];
else temp[k++]=a[s++];
}
while(s<=mid) temp[k++]=a[s++];
while(e<=tail) temp[k++]=a[e++];
k=0;
for(int i=head;i<=tail;i++) a[i]=temp[k++];
}
void m_sort(int head,int tail){
int mid=(head+tail)/2;
if(head<tail){
m_sort(head,mid);
m_sort(mid+1,tail);
merge(head,tail);
}
return;
}
example
Just in the process of combining, as long as this number is smaller than another number, the number smaller than this number must be smaller than the other number, so add mid-s+1 to the answer.
void f(int l,int r,int &max1,int &max2){
if(l==r) max1=a[l],max2=inf;
else if(l+1==r){
max1=max(a[l],a[r]);
max2=min(a[l],a[r]);
}
else{
int mid=(l+r)/2;
int lmax1,lmax2;
f(l,mid,lmax1,lmax2);
int rmax1,rmax2;
f(mid+1,r,rmax1,rmax2);
if(lmax1>rmax1){
max1=lmax1;
max2=max(lmax2,rmax1);
} else {
max1=rmax1;
max2=max(rmax2,lmax1);
}
}
}
We just need to compare when we divide
3. Find two elements at a time
void f(int l,int r,int &min1,int &min2){
if(l==r) min1=a[l],min2=inf;
else if(l+1==r){
min1=min(a[l],a[r]);
min2=max(a[l],a[r]);
}
else{
int mid=(l+r)/2;
int lmin1,lmin2;
f(l,mid,lmin1,lmin2);
int rmin1,rmin2;
f(mid+1,r,rmin1,rmin2);
if(lmin1>rmin1){
min1=rmin1;
min2=min(rmin2,lmin1);
} else {
min1=lmin1;
min2=min(lmin2,rmin1);
}
}
}
Similarly, just compare the smaller decimals
Binary search
Template code
int f(int l,int r,int x){
while(l<r){
int mid=l+r>>1;//divide half-and-half
if(a[mid]<x) l=mid+1;
else r=mid;
}
if(a[l]==x) return l;
else return -1;
}
example
- Lower bound of binary search
(1) Compare with two points
int f() {
int l = 0, r = n + 1;
while (l + 1 < r) {
int mid = (r + l) / 2;
if (a[mid] >= x)
r = mid;
else
l = mid;
}
return r;
}
(2) Use function
Lower bound of binary search
lower_ Bound (begin, end, Num): find the first number greater than or equal to num from the beginning position to the end-1 position of the array, find the address to return the number, and return end if it does not exist. Subtract the starting address begin from the returned address to get the index of the found number in the array.
Upper bound of binary search
upper_ Bound (begin, end, Num): from the beginning position to the end-1 position of the array, find the first number greater than num, find the address to return the number, and return end if it does not exist. Subtract the starting address begin from the returned address to get the index of the found number in the array.
code
Lower bound of binary search
#include<bits/stdc++.h>
using namespace std;
const int Max=1e6+5;
int a[Max];
int main() {
int n,m;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
scanf("%d",&m);
printf("%d",lower_bound(a+1,a+n+1,m)-a);
return 0;
}
Upper bound of binary search
#include <bits/stdc++.h>
using namespace std;
const int Max = 1e6 + 5;
int a[Max];
int main() {
int n, m;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
scanf("%d", &m);
printf("%d", upper_bound(a + 1, a + n + 1, m) - a - 1);
return 0;
}
int f(int l,int r,int x){
while(l+1<r){
int mid=l+r>>1;
if(a[mid]<x) l=mid;
else r=mid;
}
if(abs(x-a[l])<=abs(x-a[r])) return a[l];
else return a[r];
}
After sorting, you just need to compare the distance to find the element closer and return
#include<bits/stdc++.h>
using namespace std;
const int Max=1e6+5;
int n,m,a[Max];
int f(int l,int r,int find){
while(l<=r){
int mid=l+r>>1;
if(a[mid]==find) return a[mid];
else if(a[mid]<find) l=mid+1;
else r=mid-1;
}
return 0;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
scanf("%d",&m);
for(int i=1;i<n;i++){
if(a[i]>m/2) break;//prune
if(f(i+1,n,m-a[i])){
printf("%d %d",a[i],f(i+1,n,m-a[i]));
return 0;
}
}
printf("No");
}
Using dichotomy, the second cycle in the double cycle is changed to dichotomy optimization time
Indirect dichotomy
Indirect dichotomy refers to the need to change the mid of dichotomy into comparison value with cheak, which depends on the situation
example
1.Finding the zero point of a function by dichotomy
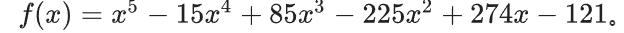
In this question, cheak is written from the above figure
double check(double x){
return pow(x,5)-15*pow(x,4)+85*pow(x,3)-225*pow(x,2)+274*x-121;
}


The following code can be written by reserving 6 bits, f (1.5) > 0 and f (2.4) < 0
while(1){
double mid=(l+r)/2;
if(fabs(check(mid))<1e-6){
printf("%.6lf",mid);
return 0;
}
else if(check(mid)<=-1e-6) r=mid;
else l=mid;
}
- Solution of univariate cubic equation
cheak can be written from ax3+bx2+cx+d = 0
The dichotomous range can be seen from the range of the root between - 100 and 100
#include<bits/stdc++.h>
using namespace std;
double a,b,c,d;
double cheak(double x){
return a*pow(x,3)+b*x*x+c*x+d;
}
int main(){
scanf("%lf %lf %lf %lf",&a,&b,&c,&d);
for(double i=-100;i<100;i++){
if(cheak(i)==0){
printf("%.2lf ",i);
continue;
}
if(cheak(i)*cheak(i+1)<0){
double l=i,r=i+1,mid;
while(r-l>0.001){
mid=(l+r)/2;
if(cheak(mid)*cheak(l)<0) r=mid;
else l=mid;
}
printf("%.2lf ",mid);
}
}
return 0;
}
- Network cable Supervisor
We need to cut the network cable, so we can cut the length in half.
Just write cheak to return the number of cut roots compared with the input
#include<bits/stdc++.h>
using namespace std;
const int Max=1e4+5;
int a[Max],n,k;
int cheak(int mid){
int sum=0;
for(int i=1;i<=n;i++) sum+=a[i]/mid;//Cut wire
return sum;
}
int main(){
scanf("%d %d",&n,&k);
double x;
int maxl=0;
for(int i=1;i<=n;i++){
scanf("%lf",&x);
x=int(x*100+0.5);//Turn centimeter
if(x>maxl) maxl=x;//Find the longest
a[i]=x;
}
int l=1,r=maxl,mid,ans;
while(l<r){
mid=l+r+1>>1;//Average length
if(cheak(mid)>=k) l=mid,ans=mid;//Save answer
else r=mid-1;
}
if(cheak(l)>=k) printf("%.2lf",l/100.0);
else printf("0.00");
return 0;
}
- Monthly expenses
From the meaning of the question, we can understand that we can divide the number of fajo months in half, and then compare it with the input. If it is too large, the left pointer is too small, and if it is too small, the right pointer is too large
#include<bits/stdc++.h>
using namespace std;
const int Max=1e5+5;
int a[Max],n,m,maxn,sum;
int cheak(int mid){
int sum=0,fajo=1;
for(int i=1;i<=n;i++){
if(sum+a[i]>mid) fajo++,sum=a[i];
else sum+=a[i];
}
return fajo;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
maxn=max(maxn,a[i]),sum+=a[i];
}
int l=maxn,r=sum;
while(l<r){
int mid=l+r>>1;
if(cheak(mid)>m) l=mid+1;
else r=mid;
}
printf("%d",r);
return 0;
}
Divide and conquer thinking problem
1.Jump a house in the river
We can divide the number of stones here, and there will be a cheak
bool cheak(int x) {
int d = 0, cnt = 0;
for (int i = 1; i <= N; i++) {
if (a[i] - d < x) cnt++;
else d = a[i];
}
if (L - d < x) cnt++;
return cnt <= M;
}
Add the split template
while (l + 1 < r) {
int mid = (l + r) / 2;
if (cheak(mid)) l = mid;
else r = mid;
}
2.An inflated stick
We can see that the problem is very encircled
The inverse sine function is in cmath
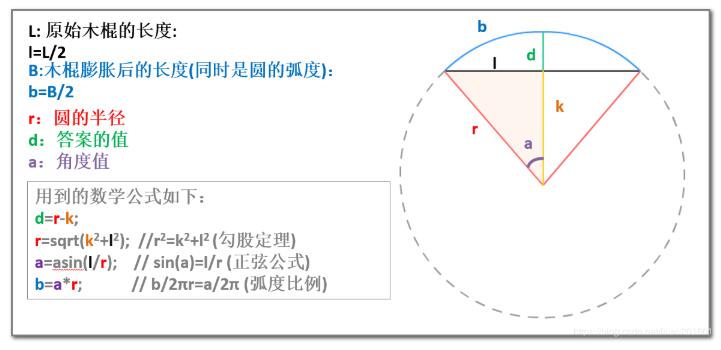
But after seeing the prompt, I immediately understood the degree of the center angle of the dichotomy circle
while(ri-le>1e-7){
double mid=(le+ri)/2;
double r=(mid*mid+l*l)/(2*mid);
double ll=r*asin(l/r);
if(ll>L) ri=mid;
else le=mid;
}
You have this binary code
**You can make 1e-7 smaller to make it more accurate, but it takes longer
**
queue
Using array simulation
Handwritten
- empty
void clear(){
r=l;
}
- Judge whether the queue is empty
bool empty(){
return l==r;//1 is empty
}
- Insert integer x at the end of the line
void push(int x){
a[r]=x;
r++;
}
4. The first element of the team goes out of the queue
void pop(){
l++;
}
- Gets the value of the first element of the queue.
int front(){
return a[l];
}
example
STL encapsulation function
definition
Queue < type (can be connector, queue) > function name
Use function
q.empty() If the queue is empty, return true,Otherwise return false q.size() Returns the number of elements in the queue q.pop() Deletes the first element of the queue without returning its value q.front() Returns the value of the first element of the queue without deleting it q.push() Push in new elements at the end of the team q.back() Returns the value of the end of queue element, but does not delete it
Explain in detail
- front(): returns the reference of the first element in the queue. If queue is a constant, a constant reference is returned; If queue is empty, the return value is undefined.
- back(): returns the reference of the last element in the queue. If queue is a constant, a constant reference is returned; If queue is empty, the return value is undefined.
- Push (const T & obj): add a copy of the element at the end of the queue. This is done by calling the member function push of the underlying container_ Back().
- Push (T & & obj): add elements at the end of the queue in a moving way. This is done by calling the member function push of the underlying container with an R-value reference parameter_ Back().
- pop(): delete the first element in the queue.
- size(): returns the number of elements in the queue.
- empty(): returns true if there is no element in the queue.
- Empty (): call T's constructor with the parameters passed to empty (), and generate an object at the end of the queue.
- Swap (queue &other_q): the elements and parameters in the current queue
- Element exchange in queue. They need to contain elements of the same type. You can also call the global function template swap() to complete the same operation.
example
#include<bits/stdc++.h>
using namespace std;
queue<int>s1;
queue<int>s2;
int main(){
int m,n,k;
scanf("%d %d %d",&m,&n,&k);
for(int i=1;i<=m;i++) s1.push(i);
for(int i=1;i<=n;i++) s2.push(i);
while(k--){
printf("%d %d\n",s1.front(),s2.front());
s1.push(s1.front());
s2.push(s2.front());
s1.pop();
s2.pop();
}
return 0;
}
Output separately using two pairs of columns
2. Number set
#include<bits/stdc++.h>
using namespace std;
queue<long long> s1,s2,s3;
int main(){
int a,b,c,n;
scanf("%d %d",&a,&n);
s1.push(a);
int tot=0;
while(tot<n){
tot++;
b=s1.front()*2+1;
c=s1.front()*3+1;
s2.push(b);
s3.push(c);
if(s2.front()<s3.front()) s1.push(s2.front()),s2.pop();
else if(s2.front()>s3.front()) s1.push(s3.front()),s3.pop();
else s1.push(s3.front()),s2.pop(),s3.pop();
s1.pop();
if(tot==n-1) printf("%lld",s1.front());
}
return 0;
}
The original data set and 2x+1 and 3x+1 data sets are stored through three queues respectively. Then compare the size and store it in the original data set in turn
while(m<(k/n)){
if(r%n==0){
a[m++]=q.front();
q.pop();
}else q.pop();
for(int i=1;i<=p;i++){
q.push(q.front());
q.pop();
}
r++;
}
Simulate according to the requirements of the topic
4. seaport
#include<bits/stdc++.h>
using namespace std;
struct node{
int s,t;
}h;
queue<node> q;
int a[1000005],ans;
int main(){
int n,t,k,x;
scanf("%d",&n);
while(n--){
scanf("%d %d",&t,&k);
while(!q.empty()){
h=q.front();
if(h.t+86400<=t){
a[h.s]--;
if(a[h.s]==0) ans--;
q.pop();
continue;
}
break;
}
for(int j=1;j<=k;j++){
scanf("%d",&x);
h.s=x,h.t=t;
q.push(h);
a[x]++;
if(a[x]==1) ans++;
}
printf("%d\n",ans);
}
return 0;
}
Here is to enter the structure in the queue, and then use the bucket row idea to find different nationalities
Supplementary priority queue
No why, just learn more yidia for the sake of making up the number of words
definition
priority_queue<Type, Container, Functional>
Type is the data type, Container is the Container type, and Functional is the method of comparison. When you need to use a custom data type, you need to pass in these three parameters. When you use a basic data type, you only need to pass in the data type. The default is large top heap
//Ascending queue priority_queue <int,vector<int>,greater<int> > q; //Descending queue priority_queue <int,vector<int>,less<int> > q;
Be sure to add a space after Functional, otherwise it will be mistaken for moving right
function
Exactly the same as the queue
Stack
Using array simulation
Handwritten
- Empty the stack
void clear(){
l=0;
}
- Determine whether the stack is empty
bool empty(){
return l==0;
}
- Insert the integer x into the top of the stack
void push(int x){
s[l++]=x;
}
- Stack top element out of stack
void pop(){
l--;
}
- Gets the value of the top element of the stack
int top(){
return s[l-1];
}
example
STL encapsulation function
definition
Stack < data type > function name
function
size( ) Returns the number of elements in the stack top( ) Returns the element at the top of the stack pop( ) Remove and delete elements from the stack push(e) Add element to stack e empty( ) Return when stack is empty true
example
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+5;
stack<int> s;
int n,a[maxn];
int main(){
scanf("%d",&n);
int A=1,B=1,ans=0,sum=0;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
while(B<=n){
if(A==a[B]) A++,B++,sum++,ans=max(ans,sum),sum--;
else if(!s.empty()&&s.top()==a[B]) s.pop(),B++,sum--;
else if(A<=n) s.push(A++),sum++;
else{
printf("no");
return 0;
}
ans=max(sum,ans);
}
printf("yes\n%d",ans);
return 0;
}
Use the left and right pointers to control the access of the stack
2. Bracket balance
bool f(string a){
int len=a.length(),cnt=1;
char c;
for(int i=0;i<len;i++){
if(a[i]=='('||a[i]=='[') s.push(a[i]);
else if(a[i]==')'){
if(s.empty()) return 0;
c=s.top();
if(c=='(') s.pop();
else return 0;
}
else if(a[i]==']'){
if(s.empty()) return 0;
c=s.top();
if(c=='[') s.pop();
else return 0;
}
}
if(s.empty()) return 1;
else return 0;
}
Use the stack to check why parentheses are used. If there is no match, delete them
3. Programmer input problem
Note that you can enter many "#" when entering
for(int i=0;i<l;i++){
if(s.empty()) break;
if(s.top()=='#'){
s.pop();
sum++;
ll-=2;
} else if(s.top()=='@'){
ll-=s.size();
break;
} else {
if(sum!=0) sum--,s.pop();
else {
b[z++]=s.top();
s.pop();
}
}
}
Follow the instructions to simulate
while(n--){
char ch;
cin>>ch;
if(ch=='P'){
scanf("%d %lf",&v,&c);
v0.push(v),c0.push(c);
c1=(c1*v1+v*c)/(v+v1);
v1+=v;
printf("%d %.5lf\n",v1,c1);
} else {
if(v0.size()>1){
c1=(c1*v1-v0.top()*c0.top())/(v1-v0.top());
v1-=v0.top();
v0.pop(),c0.pop();
printf("%d %.5lf\n",v1,c1);
} else printf("%d %.5lf\n",v1,c1);
}
}
Use stack LIFO to undo
5. Expression evaluation
while(ch=='+'||ch=='*'){
scanf("%d",&t);
t=t%10000;
if(ch=='+') s.push(t);
else {
t=(s.top()*t)%10000;
s.pop(),s.push(t);
}
ch=getchar();
}
while(!s.empty()){
ans=(ans+s.top())%10000;
s.pop();
}
If the search is + or *, it will jump out
6.Suffix expression evaluation
#include<bits/stdc++.h>
using namespace std;
stack <int> a;
int main(){
char s[105];
while(~scanf("%s",s)){
if(s[0]=='+'&&strlen(s)==1){
int x=a.top();
a.pop();
int y=a.top();
a.pop(),a.push(x+y);
}else if(s[0]=='-'&&strlen(s)==1){
int x=a.top();
a.pop();
int y=a.top();
a.pop(),a.push(y-x);
}else if(s[0]=='*'&&strlen(s)==1){
int x=a.top();
a.pop();
int y=a.top();
a.pop(),a.push(x*y);
}else if(s[0]=='/'&&strlen(s)==1){
int x=a.top();
a.pop();
int y=a.top();
a.pop(),a.push(y/x);
}else a.push(atoi(s));
}
printf("%d",a.top());
return 0;
}
Very classic topic. Use the stack to store numbers, judge why symbols, and perform operations
