1. Concept of reactor

1.1 definitions

If there is a key set K = {k0, k1, k2,..., kn-1}, all its elements are stored in a one-dimensional array in the order of complete binary tree, and meet the following requirements: ki < = k2i + 1 and Ki < = k2i + 2, it is called small heap (or large heap). The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.

1.2 characteristics

1. The value of a node in the heap is always not greater than or less than the value of its parent node;
2. Heap is always a complete binary tree.
3. Heap is generally regarded as a complete binary tree

1.3 type of reactor

Heap can be divided into large heap (large root heap) or small heap (small root heap) according to feature 1. A large heap is a tree in which the root node of each subtree is larger than the child node

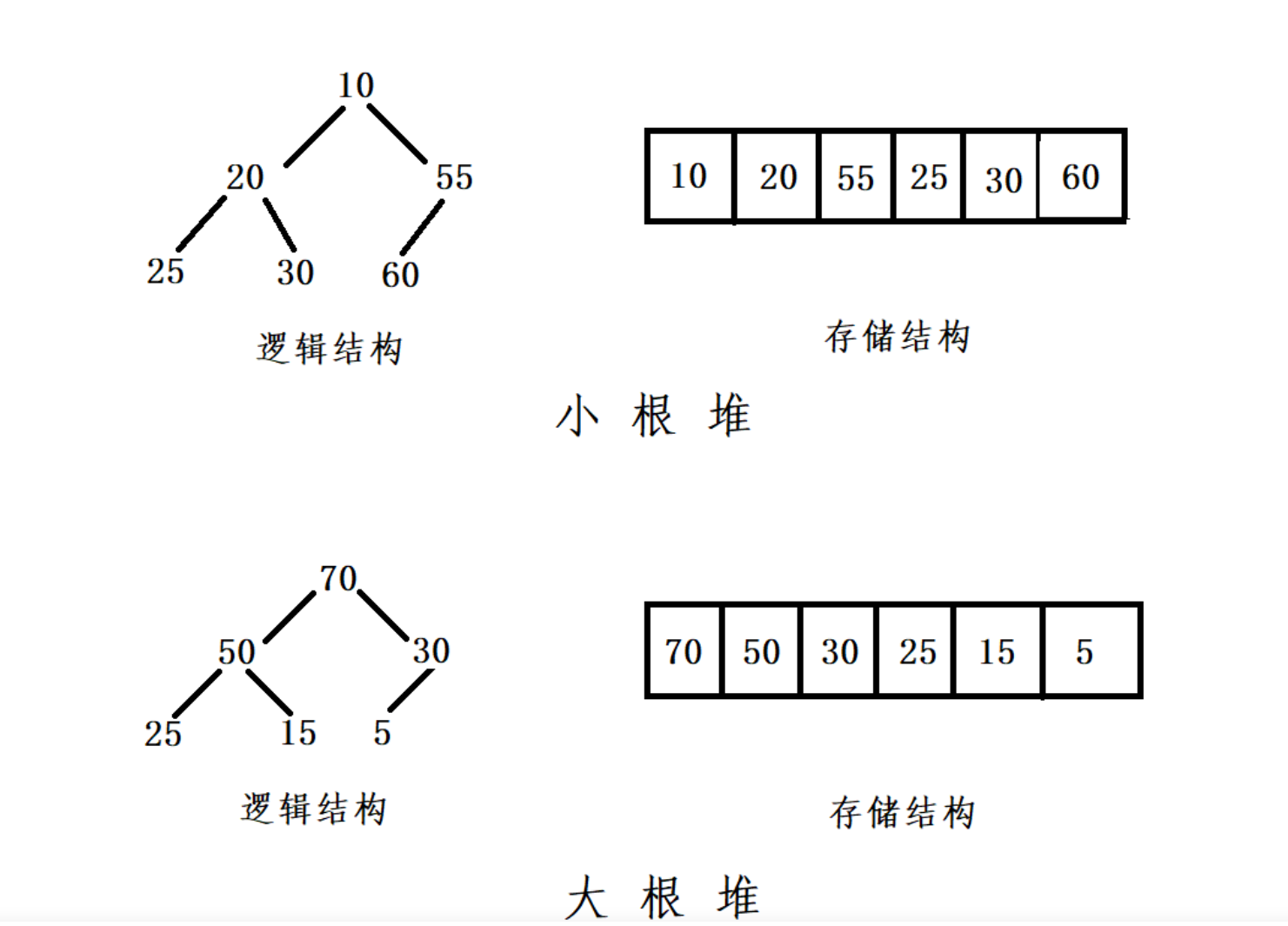
1.4 common scenarios

1. Heap is computer science A general term for a special class of data structures in. A pile is usually a tree that can be seen as a tree Complete binary tree Array object for.
2. The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap. Common heaps include binary heaps Fibonacci heap Wait.
3. Heap is a nonlinear data structure, equivalent to a one-dimensional array, with two direct successors.

2. Implementation of heap function source code

1. HeapInit

Initialize heap

void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

2. HeapDestroy

Destroy the heap and return the space occupied by the heap

void HeapDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->capacity = hp->size = 0;
}

3. HeapPush

Inserting data at the end of the array and exchanging data between the root node and the tail and adjusting the heap's data (according to the big / small heap selection up / down adjustment) keeps the heap up to its original nature.

void HeapPush(HP* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		size_t newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = realloc(hp->a, sizeof(HPDataType)*newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}

		hp->a = tmp;
		hp->capacity = newCapacity;
	}

	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}

4. HeapPop

Delete the root node and adjust the data of the heap (up / down according to the selection of large / small heap) to keep the original nature of the heap

void HeapPop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;

	AdjustDown(hp->a, hp->size, 0);
}

5. HeapEmpty

Check if the heap is empty

bool HeapEmpty(HP* hp)
{
	assert(hp);
	return hp->size == 0;
}

6.AdjustUp

Adjust upward: adjust the inserted data from the bottom up to keep the nature of the heap unchanged

void AdjustUp(int* a, int child)
{
	assert(a);

	int parent = (child - 1) >>1;
	//while (parent >= 0)
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);

			child = parent;
			parent = (child - 1) / 2;
		}
		else       break;
	}
}

7. AdjustDown

Adjust downward: adjust the inserted data downward from the root node to keep the nature of the heap unchanged

void AdjustDown(int* a, int n, int parent)//Delete the data at the top of the heap delete the root node filter value
{
	int  child = parent * 2 + 1;//Use only the left child. The subscript of the right child is left child + 1
	while (child < n)
	{
		//Choose the younger child to judge whether the right child crosses the line
		if (a[child + 1] < a[child] && child + 1 < n)	child++;

		//If the young child is smaller than his father, continue to adjust
		if (a[child] < a[parent])
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else				break;//break if you don't meet the conditions 
	}
}

8. HeapSize

Returns the number of nodes in the heap

int HeapSize(HP* hp)
{
	assert(hp);
	return hp->size;
}

9. HeapTop

Returns the size of the top element of the root node

HPDataType HeapTop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));

	return hp->a[0];
}

10. HeapPrint

Print heap (linear array)

void HeapPrint(HP* hp)
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

Implementation details

1. According to > / < in AdjustUp / AdjustDown, it is judged that it is the adjustment of large root heap / small heel heap

For example: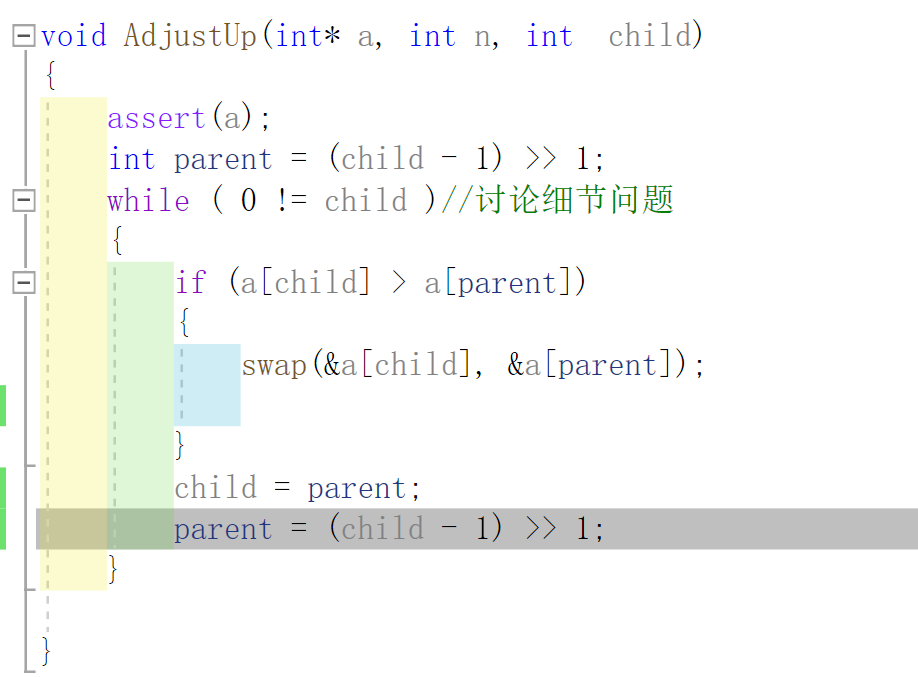

2. The judgment condition of adjustupw hile cycle is generally child > 0
3. The condition of while loop in adjustdown is generally child < n