An ordinary queue is a first in first out data structure. Elements are added at the end of the queue and deleted from the queue head. In some cases, we may need to find the maximum or minimum value in the queue. For example, a queue is used to save computer tasks. Generally, computer tasks have priority. We need to find the task with the highest priority among these computer tasks to execute first. After execution, we need to remove this task from the queue. To complete this function, ordinary queues need to traverse all elements in the queue every time, compare and find the maximum value. The efficiency is not very high. At this time, we can use a special queue to complete this demand, priority queue.

According to their different functions, priority queues can be divided into the following two types:
- Maximum priority queue: you can get and delete the maximum value in the queue
- Minimum priority queue: the smallest value in the queue can be obtained and deleted
1 maximum priority queue
We have learned about heap before, and the heap structure can easily delete the maximum value. Therefore, next, we can realize the maximum priority queue based on the heap area.
1.1 API design of maximum priority queue

1.2 code implementation of maximum priority queue
/**
* Maximum priority queue
* Implementation with heap
*/
public class MaxPriorityQueue<T extends Comparable<T>> {
//Define an array to store elements in the heap
private T[] items;
//Number of elements in the storage heap
private int N;
//Constructor initialization parameters
public MaxPriorityQueue(int capacity) {
items = (T[]) new Comparable[capacity + 1];
this.N = 0;
}
//Number of elements in the queue
public int size() {
return N;
}
//Is the queue empty
public boolean isEmpty() {
return N == 0;
}
//Queue insert element
public void insert(T t) {
//Add elements at the maximum index and increment
items[++N] = t;
//Float the element up to the correct position
swim(N);
}
//The queue floats up after the element is inserted so that it is in the correct position
public void swim(int k) {
while (k > 1) {
if (less(k / 2, k)) {
exch(k / 2, k);
}
k = k / 2;
}
}
//Delete the largest element and return this element
public T delMax() {
T max = items[1];
//Swap the position of the largest element and the last element
exch(1, N);
//Delete last element
items[N] = null;
N--;
//Sink element 1 to the correct position
sink(1);
return max;
}
//Sink after deleting elements
public void sink(int k) {
while (2 * k <= N) {
int max;
//If there are right child nodes
if (2 * k + 1 <= N) {
if (less(2 * k + 1, 2 * k)) {
max = 2 * k;
} else {
max = 2 * k + 1;
}
} else {
max = 2 * k;
}
if (!less(k, max)) {
break;
}
exch(k, max);
k = max;
}
}
//Compare element sizes
public boolean less(int i, int j) {
return items[i].compareTo(items[j]) < 0;
}
//Exchange element
public void exch(int i, int j) {
T temp = items[i];
items[i] = items[j];
items[j] = temp;
}
public static void main(String[] args) {
//Create minimum priority queue object
MaxPriorityQueue<String> queue = new MaxPriorityQueue<>(10);
//Save data to queue
queue.insert("G");
queue.insert("F");
queue.insert("E");
queue.insert("D");
queue.insert("C");
queue.insert("B");
queue.insert("A");
//Get the elements in the minimum priority queue through a loop
while (!queue.isEmpty()) {
String min = queue.delMax();
System.out.print(min + " ");
}
}
}
2 minimum priority queue
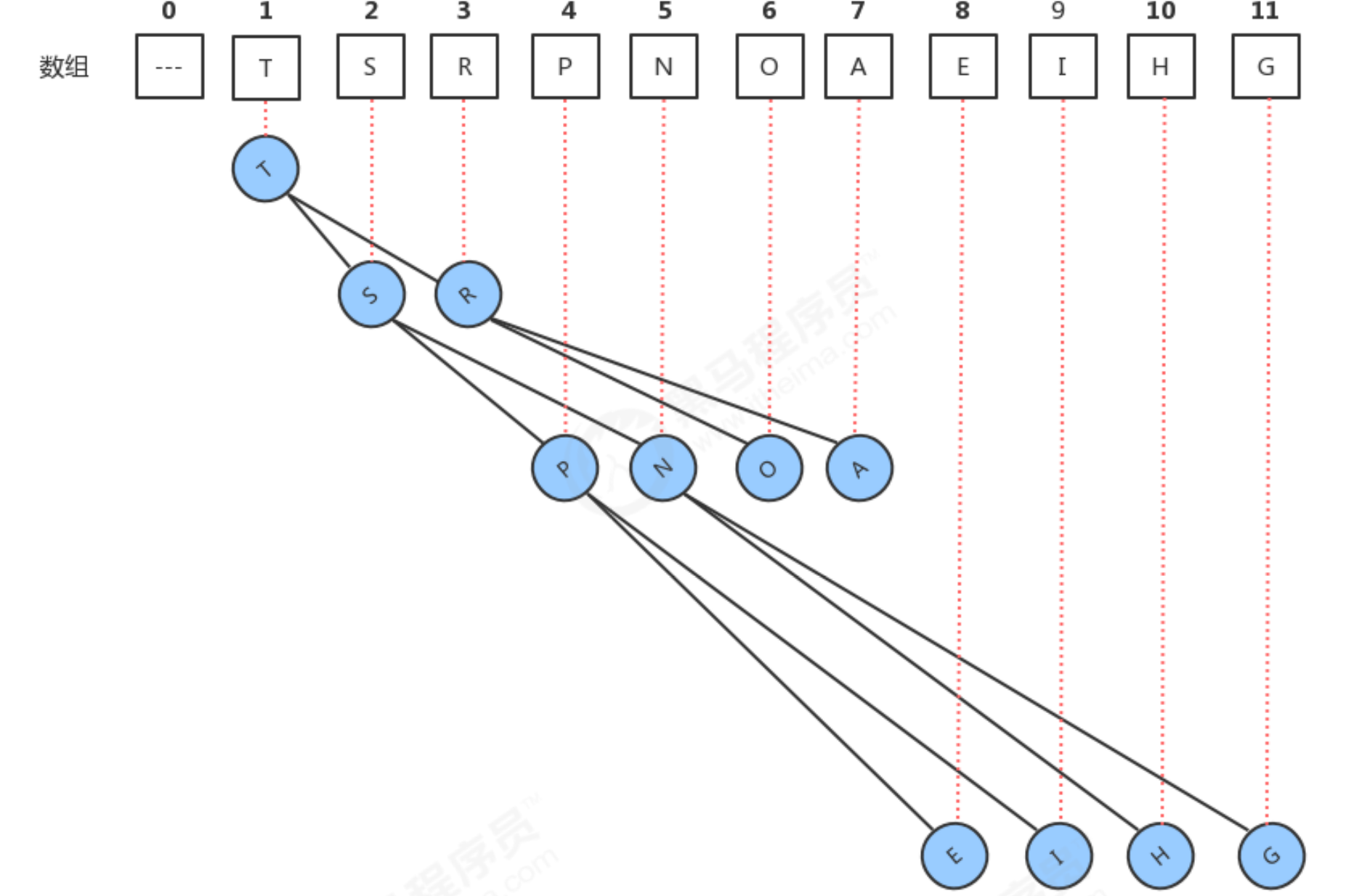
The implementation of the minimum priority queue is also relatively simple. We can also complete the minimum priority queue based on the heap. When we studied the heap earlier, the arrays storing data elements in the heap should meet the following characteristics:
- The largest element is placed at index 1 of the array.
- The data of each node is always greater than or equal to the data of its two child nodes.
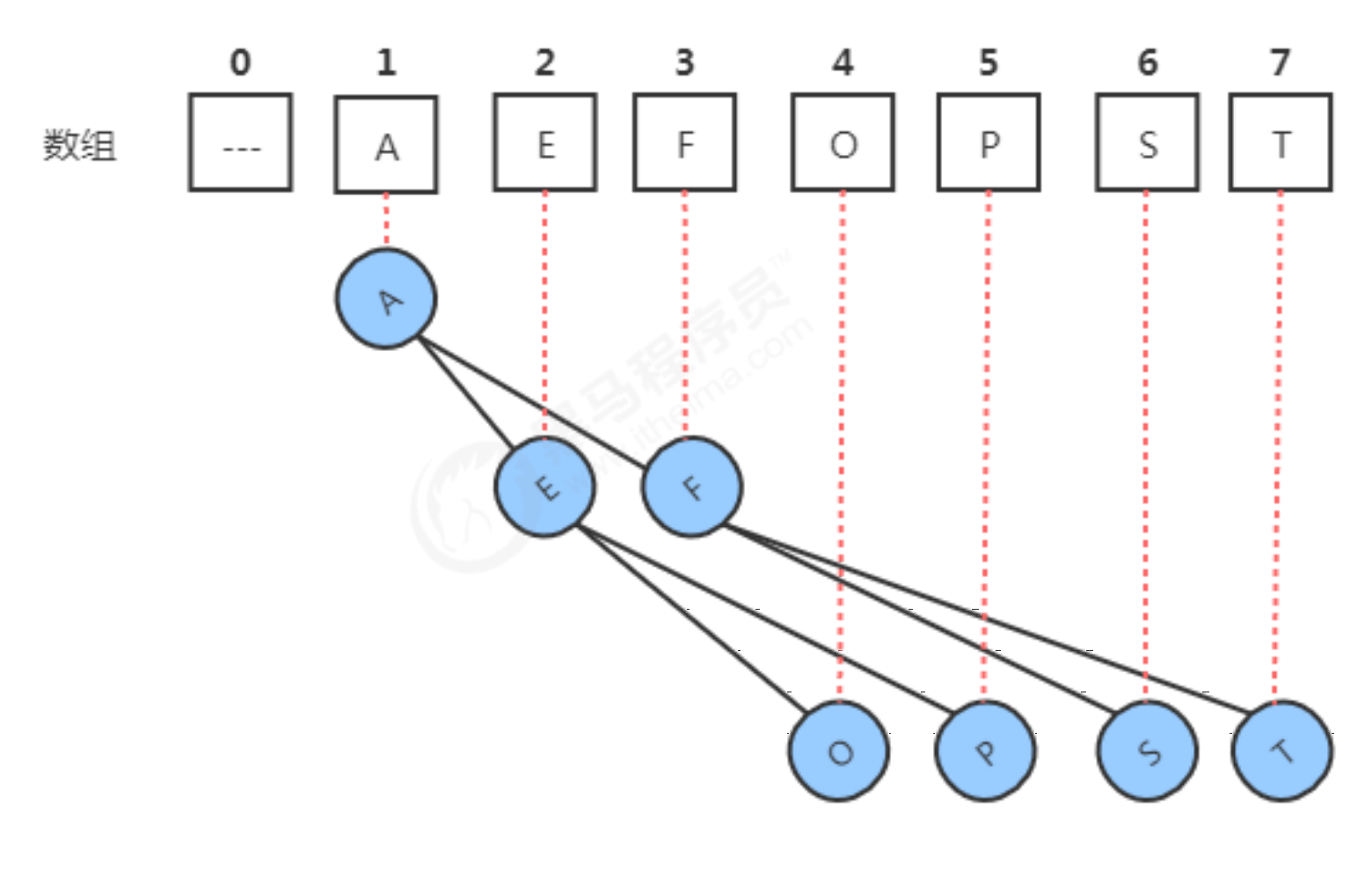
In fact, the heap we implemented before can be called the maximum heap. We can use the opposite idea to realize the minimum heap, so that the array storing data elements in the heap meets the following characteristics:
- The smallest element is placed at index 1 of the array.
- The data of each node is always less than or equal to the data of its two child nodes.
- In this way, we can quickly access the smallest data in the heap.
2.1 API design of minimum priority queue

2.2 code implementation of minimum priority queue
/**
* Minimum priority queue
* Implementation with heap
*/
public class MinPriorityQueue<T extends Comparable<T>> {
//Define an array to store elements in the heap
private T[] items;
//Record the number of elements in the heap
private int N;
//Constructor initialization parameters
public MinPriorityQueue(int capacity) {
items = (T[]) new Comparable[capacity + 1];
this.N = 0;
}
//Judge whether the queue is empty
public boolean isEmpty() {
return N == 0;
}
//Get the number of elements in the queue
public int size() {
return N;
}
//Insert elements (insert elements at the maximum index and float up to adjust the order)
public void insert(T t) {
items[++N] = t;
//Float up
swim(N);
}
//Floating up operation after inserting an element, so that the inserted k element is in another correct position in the heap
public void swim(int k) {
//Comparison between k and its parent node k/2
while (k > 1) {
if (less(k, k / 2)) {
exch(k, k / 2);
}
k = k / 2;
}
}
//Delete maximum element
public T delMin() {
//Take out the largest element with index 1
T minT = items[1];
//Swap maximum index and 1 element
exch(1, N);
//Delete element at maximum index
items[N] = null;
//Element decrement
N--;
//Now drop the element with index 1 and adjust it to the correct position
sink(1);
return minT;
}
//Sink after deleting the largest element (the last element is exchanged with the first element)
public void sink(int k) {
while (2 * k <= N) {
//Find the maximum value in the child node
//If there is a right child node
int min;
if (2 * k + 1 <= N) {
if (less(2 * k, 2 * k + 1)) {
min = 2 * k;
} else {
min = 2 * k + 1;
}
} else {
min = 2 * k;
}
//Interpret the current node and child node values
if (less(k, min)) {
break;
}
exch(k, min);
//The index points to the child node
k = min;
}
}
//Compare element sizes
public boolean less(int i, int j) {
return items[i].compareTo(items[j]) < 0;
}
//Swap element location
public void exch(int i, int j) {
T temp = items[i];
items[i] = items[j];
items[j] = temp;
}
public static void main(String[] args) {
//Create minimum priority queue object
MinPriorityQueue<String> queue = new MinPriorityQueue<>(10);
//Save data to queue
queue.insert("G");
queue.insert("F");
queue.insert("E");
queue.insert("D");
queue.insert("C");
queue.insert("B");
queue.insert("A");
//Get the elements in the minimum priority queue through a loop
while (!queue.isEmpty()) {
String min = queue.delMin();
System.out.print(min + " ");
}
}
}
3 index priority queue
In the previously implemented maximum priority queue and minimum priority queue, they can quickly access the maximum and minimum elements in the queue respectively, but they have a disadvantage that they have no way to access the objects that already exist in the priority queue through the index and update them. In order to achieve this goal, based on the priority queue, learn a new data structure, index the priority queue. Next, we take the minimum index priority queue as an example.
3.1 implementation idea of index priority queue
Step 1:
When storing data, associate each data element with an integer, such as insert (int, k, t, t). We can regard k as an integer associated with T. then our implementation needs to quickly obtain the T element in the queue through the value of k. at this time, the value of k needs to be unique.
The most intuitive idea is that we can use a T[] items array to save data elements. When inserting (int k, t t t), we can regard K as the index of the items array and put the T element at the index k of the items array. In this way, it is very convenient for us to obtain the T element according to K, and we can get the items[k] directly.
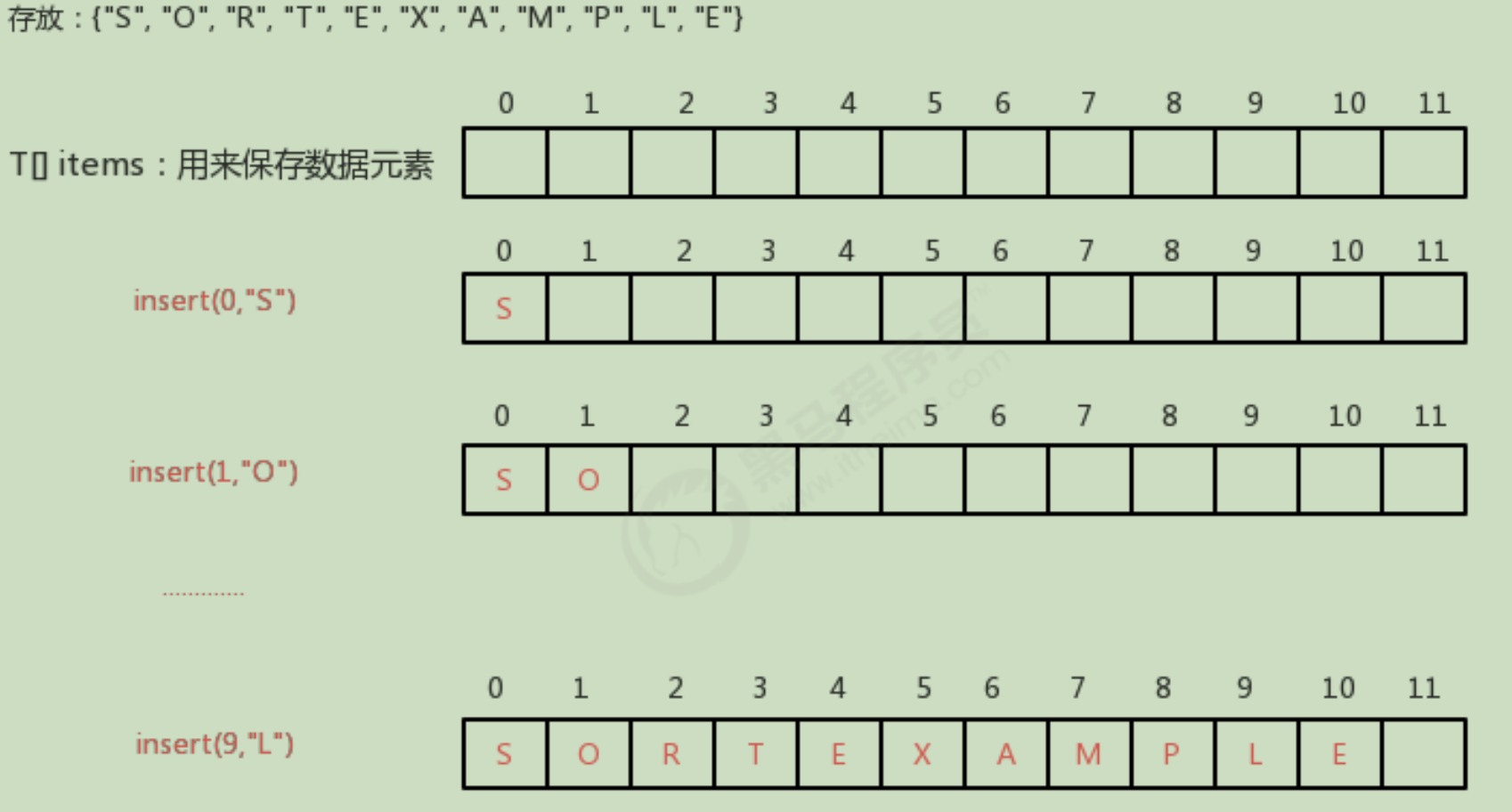
Step 2:
As a result of the completion of step 1, although we associate an integer with each element and can use this integer to quickly obtain the element, the order of the elements in the items array is random and not heap ordered. Therefore, in order to meet this requirement, we can add an array int[]pq to save the index of each element in the items array, The PQ array needs to be heap ordered, that is, the data elements items[pq[1]] corresponding to pq[1] should be less than or equal to the data elements items[pq[2]] and items[pq[3]] corresponding to pq[2] and pq[3].
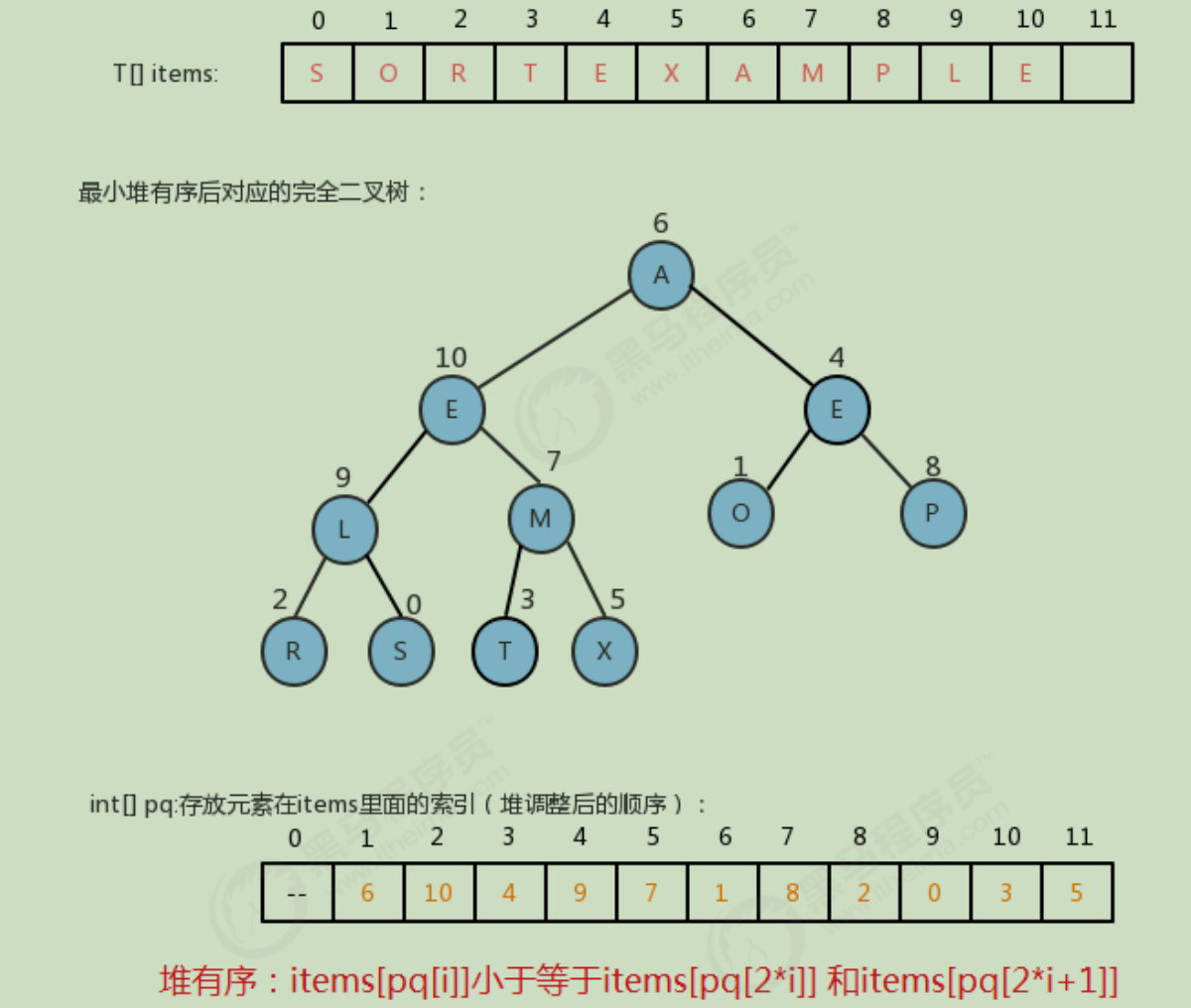
Three steps:
Through the analysis in step 2, we can find that when we make heap adjustment through floating and sinking, we actually adjust the pq array. If you need to modify the elements in items, such as making items[0] = "H", it is obvious that we need to adjust the heap of the data in pq, and adjust the position of the elements in pq[9]. But now we will encounter a problem. What we modify is the value at the 0 index in the items array. How can we quickly know the position of the element in pq[9]? The most intuitive idea is to traverse the pq array and compare each element with 0. If the current element is 0, then adjust the element at the index, but the efficiency is very low. We can add another array, int[] qp, to store the reverse order of pq. For example: in pq array: pq[1]=6; Then, in the qp array, take 6 as the index and 1 as the value, and the result is: qp[6]=1;
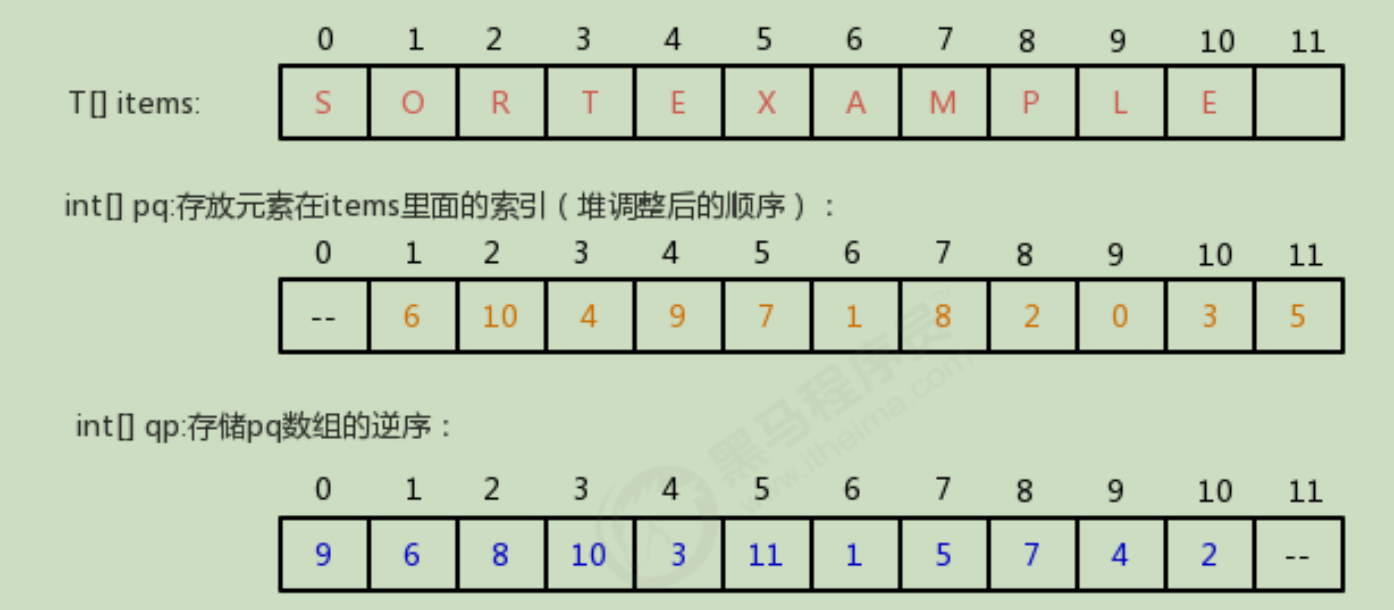
After having pq array, if we modify items[0] = "H", we can first find the index of qp in qp array through index 0: qp[0]=9, and then adjust pq[9] directly.
3.2 API design of index priority queue

3.3 code implementation of minimum index priority queue
/**
* Minimum index priority queue
*/
public class IndexMinPriorityQueue<T extends Comparable<T>> {
//Elements in the storage heap
private T[] items;
//Save the index of each element in the items array. The pq array needs to be heap ordered
private int[] pq;
//Save the reverse order of pq, with pq value as index and pq index as value
private int[] qp;
//Record the number of elements in the heap
private int N;
//Constructor
public IndexMinPriorityQueue(int capacity) {
items = (T[]) new Comparable[capacity + 1];
pq = new int[capacity + 1];
qp = new int[capacity + 1];
this.N = 0;
//The default queue does not store elements
for (int i = 0; i < qp.length; i++) {
qp[i] = -1;
}
}
//Is the queue empty
public boolean isEmpty() {
return N == 0;
}
//Queue size
public int size() {
return N;
}
//Compare size
public boolean less(int i, int j) {
//Element size at pq index
return items[pq[i]].compareTo(items[pq[j]]) < 0;
}
//Exchange element order
public void exch(int i, int j) {
//Index order in exchange pq
int temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
//Update data in qp
qp[pq[i]] = i;
qp[pq[j]] = j;
}
//Judge whether the index at k already exists
public boolean contain(int k) {
return qp[k] != -1;
}
//Index associated with the smallest element
public int minIndex() {
return pq[1];
}
//Insert element t at index i
public void insert(int i, T t) {
if (contain(i)) {
return;
}
//Save the data to the i position corresponding to the items
items[i] = t;
//Number of elements plus 1
N++;
//Store i in pq
pq[N] = i;
//Reverse order in record qp
qp[i] = N;
//Complete reactor adjustment by floating up
swim(i);
}
//Delete minimum index
public int delMin() {
//Gets the index associated with the smallest element
int minIndex = pq[1];
//Swap elements at 1 and N at pq index
exch(1, N);
//Delete inverse index
qp[pq[N]] = -1;
//Delete index stored in pq
pq[N] = -1;
//Delete element
items[minIndex] = null;
N--;
//Sinking operation
sink(1);
return minIndex;
}
//Deletes the specified index
public void delete(int i) {
//i index at pq
int k = qp[i];
//Swap k and last element index
exch(k, N);
//Delete element
items[k] = null;
//Delete inverse index
qp[pq[N]] = -1;
//Delete the index
pq[N] = -1;
//Heap adjustment
sink(k);
swim(k);
}
//Change the element associated with index i to t
public void changeItem(int i, T t) {
//Modify the element at i position in the items array to t
int k = qp[i];
//Find where i appears in pq
items[k] = t;
//Adjustment reactor
swim(k);
sink(k);
}
//Float up
public void swim(int k) {
while (k > 1) {
if (less(k, k / 2)) {
exch(k, k / 2);
}
k = k / 2;
}
}
//sink
public void sink(int k) {
while (2 * k < N) {
//Find the smallest element index in the child node
int min;
//If there are right child nodes
if (2 * k + 1 < N) {
if (less(2 * k + 1, 2 * k)) {
min = 2 * k + 1;
} else {
min = 2 * k;
}
} else {
min = 2 * k;
}
//If it is larger than the child node, no swap is needed
if (!less(k, min)) {
break;
}
exch(k, min);
k = min;
}
}
public static void main(String[] args) {
//Create index minimum priority queue object
IndexMinPriorityQueue<String> queue = new IndexMinPriorityQueue<>(10);
//Add element to queue
queue.insert(0, "A");
queue.insert(1, "C");
queue.insert(2, "F");
//Test modification
queue.changeItem(2, "B");
//Test delete
while (!queue.isEmpty()) {
int index = queue.delMin();
System.out.print(index + " ");
}
}
}
3.4 implementation of maximum index priority queue
package com.bcl.algorithm.priority;
/**
* Index maximum priority queue
*/
public class IndexMaxPriorityQueue<T extends Comparable<T>> {
//Elements in the storage heap
private T[] items;
//Store items index value
private int[] pq;
//Store the reverse order of the indexes in pq. The value of pq is the index and the index is the value
private int[] qp;
//Storing data in heap
private int N;
//Constructor initialization parameters
public IndexMaxPriorityQueue(int capacity) {
items = (T[]) new Comparable[capacity + 1];
pq = new int[capacity + 1];
qp = new int[capacity + 1];
this.N = 0;
// for (int i : qp) {
// qp[i] = -1;
// }
//The default queue does not store elements
for (int i = 0; i < qp.length; i++) {
qp[i] = -1;
}
}
//Is the queue empty
public boolean isEmpty() {
return N == 0;
}
//Queue size
public int size() {
return N;
}
public boolean max(int i, int j) {
return items[pq[i]].compareTo(items[pq[j]]) > 0;
}
//Exchange element order
public void exch(int i, int j) {
//Index order in exchange pq
int temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
//Update data in qp
qp[pq[i]] = i;
qp[pq[j]] = j;
}
//Include corresponding index
public boolean contain(int i) {
return qp[i] != -1;
}
//Maximum index
public int maxIndex() {
return pq[1];
}
//Insert element at index i
public void insert(int i, T t) {
if (contain(i)) {
return;
}
//Insert element t at items
items[i] = t;
//Self increasing number
N++;
//pq add index mapping
pq[N] = i;
//qp increases in reverse order
qp[i] = N;
//Float up and adjust the reactor sequence
swim(N);
}
//Delete maximum index
public int delMaxIndex() {
//Maximum element index found
int maxIndex = pq[1];
//Exchange element
exch(1, N);
//Delete element
items[maxIndex] = null;
//Delete inverse index
qp[pq[N]] = -1;
//Delete index
pq[N] = -1;
//Element reduction
N--;
//Sinking adjustment reactor sequence
sink(1);
return maxIndex;
}
//Delete element at index i
public void delete(int i) {
//Find the position of index i in pq and adjust the order of pq
int k = qp[i];
//Swap element positions at k
exch(k, N);
//Delete element
items[k] = null;
qp[pq[N]] = -1;
//Delete elements in pq
pq[N] = -1;
//Heap adjustment sequence
sink(k);
swim(k);
}
//Modify the value at index i to t
public void changeItems(int i, T t) {
items[i] = t;
int k = qp[i];
swim(k);
sink(k);
}
//Adjust the stacking order
public void swim(int k) {
while (k > 1) {
if (max(k, k / 2)) {
exch(k, k / 2);
}
k = k / 2;
}
}
//Adjust the stacking sequence by sinking
public void sink(int k) {
while (2 * k <= N) {
//Maximum child node found
int max;
if (2 * k + 1 <= N) {
if (max(2 * k + 1, 2 * k)) {
max = 2 * k + 1;
} else {
max = 2 * k;
}
} else {
max = 2 * k;
}
if (max(k, max)) {
break;
}
exch(k, max);
k = max;
}
}
public static void main(String[] args) {
//Create index minimum priority queue object
IndexMaxPriorityQueue<String> queue = new IndexMaxPriorityQueue<>(10);
//Add element to queue
queue.insert(0, "A");
queue.insert(1, "C");
queue.insert(2, "F");
//Test modification
queue.changeItems(2, "B");
//Test delete
while (!queue.isEmpty()) {
int index = queue.delMaxIndex();
System.out.print(index + " ");
}
}
}