Basic part
One of the most basic operations in the figure is to search which vertices can be reached from a specified vertex. For example, which cities can be reached by the high-speed railway from Wuhan, some cities can reach directly and some cities can't. Now there is a national high-speed railway simulation map. To start from a city (vertex) and move along the railway track (edge) to other cities (vertex), there are two methods to search the map: depth first search (DFS) and breadth first search (BFS). They will eventually reach all connected vertices. Depth first search is realized through stack, while breadth first search is realized through queue. Different implementation mechanisms lead to different search methods.
Depth first search
Depth first search algorithm There are the following rules: Rule 1: if possible, access an adjacent unreachable vertex, mark it, and put it on the stack. Rule 2: when rule 1 cannot be executed, if the stack is not empty, a vertex will pop up from the stack. Rule 3: if rule 1 and rule 2 cannot be executed, the whole search process is completed.
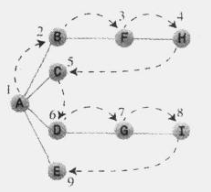
For the above figure, the application depth first search is as follows: assuming that vertex A is selected as the starting point and accessed in alphabetical order, apply rule 1, then access vertex B, mark it and put it into the stack; Apply rule 1 again, then access vertex F, and apply rule 1 again to access vertex H. At this time, we find that there is no adjacency point of vertex h. at this time, apply rule 2 and pop up h from the stack. At this time, we return to vertex F. however, we find that f also has no adjacent and unreachable vertex except h. then pop up f and return to vertex B. similarly, rule 1 cannot be applied. Apply rule 2 and pop up B. at this time, there is only vertex a in the stack, Then a has an unreachable adjacency point. All next access vertices C, but C is the end of this line, so pop it from the stack, return to a again, then access D,G,I, finally return to a, then access E, but finally return to vertex A. at this time, we find that a has no unreachable adjacency point, so we also pop it out of the stack. Now there are no vertices in the stack, so rule 3 is applied to complete the whole search process.
Depth first search is to find vertices adjacent to a vertex and have not been visited. Here, taking the adjacency matrix as an example, find the row where the vertex is located, and start from the first column to find the column with value 1 backward; The column number is the number of adjacent vertices. Check whether this vertex has not been accessed. If so, this is the next vertex to be accessed. If there is no vertex in this row that is equal to 1 (adjacent) and not accessed, then all vertices adjacent to the specified point have been accessed (which will be implemented by algorithm later).
Breadth first search
Depth first search should be as far away from the starting point as possible, while breadth first search should be as close to the starting point as possible. It first accesses all adjacent points of the starting vertex, and then accesses the far area. This search can not be realized by stack, but by queue.
Rule 1: access the next unreachable adjacency point (if any). This vertex must be the adjacency point of the current vertex, mark it, and insert it into the queue. Rule 2: if rule 1 cannot be executed because there are no unreachable adjacency points, take a vertex (if any) from the queue header and make it the current vertex. Rule 3: if rule 2 cannot be executed because the queue is empty, the search ends.
For the above figure, breadth first search is applied: starting from A, first access all vertices adjacent to A, and insert them into the queue at the same time. Now A,B,C,D and E have been accessed. At this time, the queue (from beginning to end) contains BCDE. There are no unreachable vertices adjacent to vertex A, so take B out of the queue and find the vertex adjacent to B. at this time, find F, so insert f into the queue. There are no unreachable vertices adjacent to B, so take C from the queue header. It has no unreachable adjacency points. Therefore, take out D and access G, and D has no unreachable adjacency points, so take out E. now there is FG in the queue. Take out f, access H, then take out G and access I. now there is HI in the queue. When they are taken out, it is found that there are no other vertices for access. At this time, the queue is empty and the search ends.
code implementation
Stack stack X class:
package testOffer.graphpro;
//Stack for depth first search
public class StackX {
private final int SIZE = 20;
private int[] st;
private int top;
public StackX(){
st = new int[SIZE];
top = -1;
}
public void push(int j){
st[++top] = j;
}
public int pop(){
return st[top--];
}
public int peek(){
return st[top];
}
public boolean isEmpty(){
return (top==-1);
}
}Queue for breadth first search class:
This code is by Java Architect must see network-Structure Sorting
package testOffer.graphpro;
//Queue for breadth first search
public class QueueX {
private final int SIZE = 20;
private int[] queArray;
private int front;
private int rear;
public QueueX(){
queArray = new int[SIZE];
front = 0;
rear = -1;
}
public void insert(int j){
if (rear == SIZE-1)
rear = -1;
queArray[++rear] = j;
}
public int remove(){
int temp = queArray[front++];
if (front == SIZE){
front = 0;
}
return temp;
}
public boolean isEmpty(){
return (rear+1 == front || front+SIZE-1 == rear);
}
}Figure code graph class:
package testOffer.graphpro;
public class Graph {
private final int MAX_VERTS = 20;//Represents the number of vertices
private Vertex vertexList[];//An array used to store vertices
private int adjMat[][];//The adjacency matrix is used to store edges. The array element indicates that there is no boundary, and 1 indicates that there is boundary
private int nVerts;//Number of vertices
private StackX theStack;//Using stack to realize depth first search
private QueueX queue;//Implementing breadth first search with queue
/**
* Vertex class
* */
class Vertex{
public char label;
public boolean wasVisited;
public Vertex(char label){
this.label = label;
wasVisited = false;
}
}
public Graph(){
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;//The number of initialization vertices is 0
//Initialize the adjacency matrix, all elements are 0, that is, all vertices have no edges
for (int i=0;i<MAX_VERTS;i++){
for (int j=0;j<MAX_VERTS;j++){
adjMat[i][j] = 0;
}
}
theStack = new StackX();
queue = new QueueX();
}
//Add vertices to the array, and set the access flag to wasVisited=false
public void addVertex(char lab){
vertexList[nVerts++] = new Vertex(lab);
}
//Note that the adjacency matrix is used to represent the edge, which is symmetrical, and both parts must be assigned values
public void addEdge(int start,int end){
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
//Prints the value represented by a vertex
public void displayVertex(int v){
System.out.print(vertexList[v].label+" ");
}
/**Depth first search algorithm
* 1,Check the vertices at the top of the stack with peek method
* 2,Use getadjinvisitedvertex method to find the vertex adjacent to the current stack top and not accessed
* 3,In the second step, if the return value is not equal to - 1, find the next adjacent vertex that has not been accessed, access this vertex and merge it into the stack
* If the return value in the second step is equal to - 1, it is not found and out of the stack
* */
public void depthFirstSearch(){
//Access from the first vertex
vertexList[0].wasVisited = true;//Mark as true after access
displayVertex(0);
theStack.push(0);
while (!theStack.isEmpty()){
//Find the vertex adjacent to the current vertex of the stack and not accessed
int v = getAdjUnvisitedVertex(theStack.peek());
if (v==-1){//If the current vertex value is - 1, it indicates that there are no adjacent and inaccessible vertices, and the vertices are not stacked
theStack.pop();
}else {
//Otherwise, access the next adjacent contact
vertexList[v].wasVisited = true;
displayVertex(v);
theStack.push(v);
}
}
//After accessing the stack, reset all flag bits to false
for (int i=0;i<nVerts;i++){
vertexList[i].wasVisited = false;
}
}
//Find a vertex that is adjacent to a vertex and is not accessed
public int getAdjUnvisitedVertex(int v){
for (int i=0;i<nVerts;i++){
//The v vertex is adjacent to the i vertex and is not accessed
if (adjMat[v][i]==1&&vertexList[i].wasVisited==false)
return i;
}
return -1;
}
/**Breadth first search
* 1,Use the remove method to check the top of the stack
* 2,An attempt was made to find an adjacency point where this vertex has not been accessed
* 3,If not found, the vertex is out of line
* 4,If such a vertex is found, access the vertex and put it in the queue
* */
public void breadthFirstSearch(){
vertexList[0].wasVisited = true;
displayVertex(0);
queue.insert(0);
int v2;
while(!queue.isEmpty()){
int v1 = queue.remove();
while ((v2 =getAdjUnvisitedVertex(v1))!=-1){
vertexList[v2].wasVisited = true;
displayVertex(v2);
queue.insert(v2);
}
}
//After the search, initialize to facilitate the next search
for (int i=0;i<nVerts;i++){
vertexList[i].wasVisited = false;
}
}
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addEdge(0,1);//AB
graph.addEdge(1,2);//BC
graph.addEdge(0,3);//AD
graph.addEdge(3,4);//DE
System.out.println("Depth first search algorithm:");
graph.depthFirstSearch();
System.out.println();
System.out.println("---------------");
System.out.println("Breadth first search algorithm:");
graph.breadthFirstSearch();
}
}